 |
Условные обозначения блок-схем
|
|
|
|
Лекция №2
Принцип обработки информации. Алгоритмы и способы их описания.
Обработка информации. Виды обработки.
Обработка информации – преобразование информации из одного вида в другой, осуществляемое по строгим формальным правилам.
Обработка информации – это решение информационной задачи, или процесс перехода от исходных данных к результату.
Обработка информации бывает двух типов:
1. обработка, связанная с получением нового содержания, новой информации;
2. обработка, связанная с изменением формы информации, но не изменяющая её содержания.
Примеры обработки информации
| Примеры | Входная информация | Выходная информация | Правило |
| Вычисление значения арифметического выражения (математические вычисления) | Числовые величины, знаки выполняемых действий | Числовая величина (значение выражения) | Правила арифметики |
| Перевод текста с одного естественного языка на другой (кодирование) | Исходный текст на языке оригинала | Текст, переведенный на требуемый язык | Лингвистические правила |
| Получение секретных сведений (кодирование) | Зашифрованное сообщение. | Дешифрованный текст | Свое в каждом конкретном случае |
| Разработка версии экспертом-криминалистом (логическое рассуждение) | Перечень имеющихся фактов | Версия преступления | Формально не определено |
| Сортировка по алфавиту (структурирование) | Исходный список (неупорядоченный) | Отсортированный список | Алгоритм сортировки |
| Постановка диагноза болезни (логическоерассуждение) | Жалобы пациента + результаты анализов | Диагноз | Свое в каждом конкретном случае. Основано на знаниях и опыте врача |
| Фильтрация информации по определенным критериям (поиск) | Массив информации | Часть исходного массива, отвечающего критериям | Алгоритм поиска. |
Во всех примерах требуется наличие определенного алгоритма.
|
|
|
Слово алгоритм (от латинского algorithmi) появилось как транслитерация имени арабского математика аль Хорезми (жил в 787 ÷ 850 гг. н. э.). Алгоритм – одно из самых фундаментальных понятий информатики, математики и ряда других дисциплин.
В свое время Мухаммед аль Хорезми предложил правила выполнения арифметических вычислений с многозначными числами. Именно их в Европе стали называть алгоритмами. Позже понятие алгоритм приобрело более широкий смысл и стало использоваться применительно к различным областям человеческой деятельности, когда для достижения какого-либо результата требовалось выполнение определенной последовательности действий.
В различных источниках понятие алгоритма определяется по-разному. Можно встретить такие определения:
Алгоритм – точное предписание о выполнении в определенном порядке некоторой системы операций, позволяющее решить совокупность задач определенного класса.
Алгоритм – совокупность правил, определяющих эффективную процедуру решения любой задачи из некоторого заданного класса задач.
Алгоритм – конечный набор правил, позволяющий чисто механически решить любую конкретную задачу из некоего класса однотипных задач.
Алгоритм – понятное и точное предписание исполнителю выполнить конечную последовательность команд, приводящую от исходных данных к искомому результату.
При очевидном внешнем различии в этих определениях их суть одинакова. Анализируя их можно сформулировать основные свойства, которыми обладают алгоритмы.
- Все команды (предписания) должны быть понятны исполнителю алгоритма. (Понятность алгоритма)
- Алгоритм должен выполняться за конечное число шагов. (Результативность или как иногда говорят конечность алгоритма)
- В результате выполнения алгоритма для всех допустимых исходных данных должен получаться правильный результат. (Корректность алгоритма)
- Все решения на выполнение тех или иных действий должен определять составитель алгоритма. Исполнитель не должен принимать самостоятельно каких-либо решений. (Определенность алгоритма)
- Каждый шаг алгоритма должен определяться одной командой- предписанием. (Дискретность алгоритма)
- Алгоритм должен быть применим для работы с большим количеством исходных данных. (Массовость алгоритма)
Формы представления алгоритмов могут быть весьма разнообразны. К основным, однако, обычно относят три:
|
|
|
- словесное описание
- блок-схема.
- текст программы.
Словесное описание, как правило, излишне громоздко и совершенно не наглядно. Его целесообразно использовать на этапе разработки задания для составления блок-схем.
Блок-схема алгоритма (программы) – ее изображение в виде условных графических обозначений с примечаниями. Блок-схема позволяет выявить общую последовательность действий и структуру их организации (от латинского слова structura – взаиморасположение и связь составных частей сложного объекта).
При структурном анализе возможных способов организации действий в ходе выполнения алгоритмов были выявлены три основные (базовые) алгоритмическиеструктуры:
- структура следования;
- структура ветвления;
- структура повторения «цикла».
В зависимости от сложности решаемых задач количество условных графических обозначений, используемых для представления алгоритмов в виде блок-схем, может быть достаточно большим. Для решения задач нам достаточно лишь их части.
Условные обозначения блок-схем
| Условное обозначение | Обозначаемый процесс | |||
| Начало / конец | |||

| Ввод / вывод | |||

| Действие (операция преобразования информации) | |||
 
| Проверка условия с последующим разветвлением | |||

| Линия следования (связь отдельных частей блок-схемы) |
Используя приведенные условные обозначения можно графически представить основные алгоритмические структуры.
Структура следования.

| Следование – это однозначная (еще говорят) линейная структура. Каждый блок может обозначать как простую команду, так и последовательность команд и обязательно иметь один вход и один выход |
|
|
|
Структуры ветвления.
 Полное ветвление
Полное ветвление
| Ветвление – разделение алгоритма на два пути (две ветви) по некоторому условию с дальнейшим выходом на общее продолжение. |
 Неполное ветвление
Неполное ветвление
| Неполная форма ветвления имеет место, если ветви «иначе» нет. |
Структуры повторения.
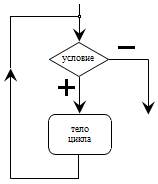 Цикл с предусловием
Цикл с предусловием
| Цикл – повторение некоторой группы действий по условию Цикл с предусловием организует выполнение одного оператора заранее неизвестное число раз. Выход из цикла осуществляется, если окажется ложным логическое выражение, определяющее условие. Поскольку условие проверяется перед началом каждого очередного выполнения тела цикла, то оно может не выполняться ни разу. |
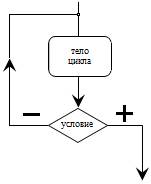 Цикл с послеусловием
Цикл с послеусловием
| Цикл с послеусловием организует выполнение одного или нескольких операторов заранее неизвестное число раз. Выход из цикла осуществляется, если окажется истинным логическое выражение, определяющее условие. Поскольку условие проверяется после каждого очередного выполнения тела цикла, то оно будет выполнено хотя бы один раз обязательно. |
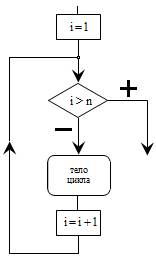 Цикл с параметром
Цикл с параметром
| Цикл с параметром организует выполнение одного оператора заранее известное число раз При выполнении этого оператора: - вычисляются и запоминаются начальное и конечное значения параметра цикла; - параметру цикла присваивается начальное значение; - текущее значение параметра сравнивается с его конечным значением; - пока параметр меньше или равен конечному значению, выполняется очередной раз выполняется тело цикла; - когда параметр превысит величину конечного значения, происходит выход из цикла. |
Из этих базовых структур можно строить блок-схемы алгоритмов любой сложности, используя два способа их соединения между собой:
|
|
|
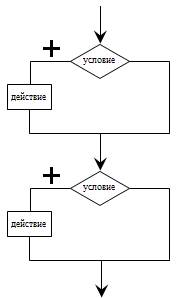 Последовательное соединение структур Последовательное соединение структур
|  «Вложение» структур «Вложение» структур
|
Элементы алгебры логики
Арифметика – наука о числах и операциях над ними. В результате выполнения операций получается число.
Алгебра – раздел элементарной математики, изучающий более широкий круг объектов (величины, функции …).
Алгебра логики. Объектом ее рассмотрения являются высказывания.
Это логическая система, применяемая во всех современных компьютерах, известная как алгебраическая система Буля.
Она была разработана в XIX веке английским математиком Джорджем Булем, который сумел решить проблему, занимавшую еще Лейбница. Ему удалось привнести в логические построения математические методы. В 1847 году Буль написал статью «Математический анализ логики», а в1854 году развил свои идеи в работе под названием «Исследование законов мышления». В результате появилась своеобразная алгебра – система обозначений и правил, применимых ко многим объектам, от чисел и букв до целых предложений. Появилась возможность кодировать подлежащие доказательству высказывания (утверждения)
Вообще под высказыванием принято понимать любое утверждение, о котором имеет смысл говорить, что оно истинно или ложно.
Рассмотрим для примера несколько утверждений:
1. Число 13 – простое
2. Число 13 – несчастливое;
3. Число 13 – четное.
Утверждение (1), истинно и его можно считать высказыванием.
Утверждение (3) – тоже высказывание, но ложное.
Утверждение (2) нельзя считать высказыванием, поскольку проверить его истинность или ложность невозможно.
Для работы с высказываниями вводятся свои операции. Пользуясь этими операциями (их принято называть логическимисвязками) можно образовывать новые высказывания.
К таким связкам относятся:
- частица «не»;
- союзы «или», «и»;
- конструкция «если …, то …».
В вычислительной технике используется четыре основные логические связки (операции), но предметом нашего рассмотрения будут только две из них.
Логическое сложение (сумма высказываний). Новое высказывание может быть образовано из данных с помощью союза «или». Например, из высказываний «этот треугольник является остроугольным» и «этот треугольник является прямоугольным» можно составить высказывание «этот треугольник является остроугольным или прямоугольным».
В системах программирования для записи операции логического сложения используется английский аналог союза «или» – «or».
Ее принято обозначать одним из приведенных ниже способов:
ü А + В
ü А or B
Логическое умножение (произведение высказываний). Из данных высказываний новое высказывание можно получить с помощью союза «и». Например, из высказываний «2 – простое число» и «2 – четное число» можно составить высказывание «2– это простое и четное число».
|
|
|
Ее принято обозначать одним из приведенных ниже способов:
В системах программирования для записи операции логического умножения используется английский аналог союза «u» – «and».
Ее принято обозначать одним из приведенных ниже способов:
ü А · В
ü А & В
ü А and B
Объединяя несколько высказываний знаками логических операций, можно составлять логические выражения. Причем высказывания (логические величины), входящие в состав выражения, могут рассматриваться как логические аргументы, а результат выполнения над ними указанной в выражении логической операции, как логическая функция (иногда их называют Булевыми функциями).
Булевы функции, как и их аргументы, принимают лишь одно из двух возможных значений:
- True, «1»(если она истинна);
- False, «0»(если она ложна).
Определение значения логической функции является занятием специфичным, а запись полученного результата процесс достаточно трудоемкий. Например, чтобы предсказать возможное значение логической функции «и», то есть определить результат логического умножения двух простых высказываний (аргументов), придется учесть, что оба аргумента могут приобретать как значение «0» так и «1» и каждое из этих значений логического аргумента должно рассматриваться со всеми возможными значениями другого аргумента. Поэтому табличный способ будет наиболее оптимальным для наглядного отображения результата.
Булеву функцию задают с помощью таблицы ее значений, которую иногда называют таблицей истинности.
Таблица истинности операции ИЛИ (or)
| А | В | АorВ |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Таблица истинности операции И (and)
| А | В | АandВ |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Используя возможности алгебры логики можно лаконично записывать результат решения логических задач различного содержания. При этом следует иметь в виду, что любая задача, ответом на которую будет заключение «ДА» или «НЕТ» является логической задачей, хотя перед тем, как непосредственно приступить к ее решению иногда приходится производить вычисления (решать расчетную задачу).
Разберем порядок использования возможностей алгебры логики применительно к задачам геометрического содержания.
Задача 1. Даны три отрезка определенной длины. Следует выяснить, могут ли они являться сторонами треугольника.
Очевидно, что положительное заключение можно будет сделать только при том условии, что сумма длин двух любых отрезков будет больше чем длина третьего отрезка. Если длины отрезков a, b, c то условия могут быть записаны в виде системы неравенств

При невыполнении хотя бы одного из этих условий треугольник построить будет невозможно. Другими словами, чтобы высказывание (утверждение) «эти отрезки могут быть сторонами треугольника» было истинным, все три условия должны выполняться одновременно.
Средства алгебры логики позволяют представить все приведенные выше рассуждения в виде логического выражения, истинности которого достаточно для того, чтобы сделать положительное заключение.
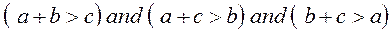
Задача 2. Дан треугольник со сторонами a, b, c. Необходимо выяснить, является ли он равнобедренным.
Очевидно, что положительное заключение можно будет сделать только при условии, что найдутся любые две стороны одинаковой по длины. Иными словами должно быть выполнено одно из перечисленных ниже условий.

При выполнении хотя бы одного из этих условий треугольник будет равнобедренным. Чтобы высказывание (утверждение) «этот треугольник является равнобедренным» было истинным достаточно выполнения одного условия.
По аналогии с предыдущим примером сформируем логическое выражение, истинности которого достаточно для того, чтобы можно было считать треугольник равнобедренным.
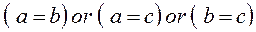
Задача №3. Для функции y = f(x), заданной формулой, выяснить, при каких значениях аргумента х она будет определена.
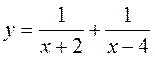
Совершенно очевидно, что значении аргумента (–2) и (4) не приемлемы, поскольку приводят к обнулению знаменателя. Поэтому оба эти значения следует исключить. Появляются два условия, выполнение которых является обязательным
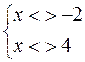
Их можно свести к одному логическому выражению:
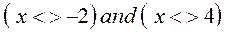
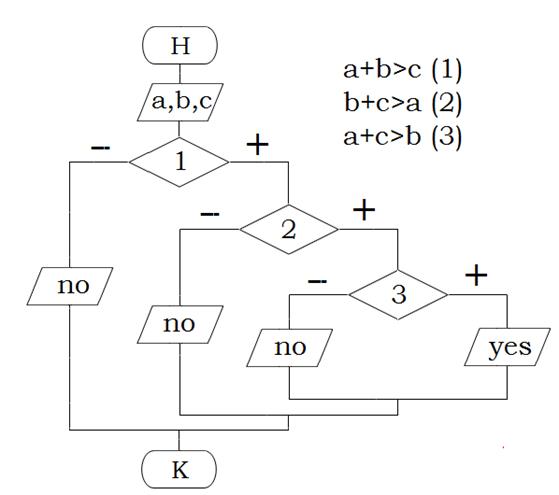 Алгоритм решения любой из приведенных задач можно представить в виде блок-схемы. Например, решая задачу №1, мы должны последовательно рассмотреть выполнение трех условий, что приведет к показанной ниже блок-схеме.
Алгоритм решения любой из приведенных задач можно представить в виде блок-схемы. Например, решая задачу №1, мы должны последовательно рассмотреть выполнение трех условий, что приведет к показанной ниже блок-схеме.
Для задачи №2 блок-схема будет выглядеть так:

Представить блок-схему алгоритма задачи №3 попробуйте самостоятельно.
|
|
|



