 |
Вопрос 31. Простое число. Количество простых чисел. Основная теорема арифметики.
|
|
|
|
Вопрос 18. Шифр ГОСТ 28147-89: параметры, общая схема шифрования и дешифрования, функция раунда, алгоритм развертки ключей, использование шифра в РФ.
Разработан в 80-ч годах
r=64 бит (длина сообщения)
k=256=8 х 32 (разбивается на 8-мь 32-х битных блока)
N=32 (число раундов)
Основой является сеть Feistel

F-функция раунда – Ri-1 складывается по mod 232 c Ki, зтемрезультат разбивается на 8-мь 4-х битовых последовательностей каждая из которых поступает на вход своего узла таблицы замен (в порядке возрастания старшинства битов), называемого ниже S-блоком. Каждый S-блок представляет собой перестановку чисел от 0 до 15 (конкретный вид S-блоков в стандарте не определен). Выходы всех восьми S-блоков объединяются в 32-битное слово, затем всё слово циклически сдвигается влево (к старшим разрядам) на 11 битов.
Развертка ключа:
Для генерации подключей исходный 256-битный ключ разбивается на восемь 32-битных блоков: K1…K8. Ключи K9…K24 являются циклическим повторением ключей K1…K8 (нумеруются от младших битов к старшим). Ключи K25…K32 являются ключами K8…K1.
Дешифровка – так же как и шифрование, но инвертируется порядок ключей.
возможные применения (википедия)
· Использование в S/MIME (PKCS#7, Cryptographic Message Syntax).
· Использование для защиты соединений в TLS (SSL, HTTPS, WEB).
· Использование для защиты сообщений в XML Encryption.
Вопрос 23. Шифр AES: параметры, общая схема шифрования и дешифрования, подстановка, сдвиг, смешивание, смешивание с ключом, особенности использования.
AES (Rijndael)
1998 – год создания
2000 – стал стандартом
r (длина блока) = 128
k(ключ) = 128/192/256
N(раунды) = 10/12/14
входной блок копируется в массив State и дальше с ним происходят разные процедуры
|
|
|
SubBytes() – функция подстановки (операция обеспечивает нелинейность алгоритма шифрования.)
y=Ax-1 + b
y-[8x1]; A-[8x8]; x-[8x1]; b-[8x1]
ShiftRows()h аботает со строками State. При этой трансформации строки состояния циклически сдвигаются на r байт по горизонтали, в зависимости от номера строки. Для нулевой строки r = 0, для первой строки r = 1 и т. д.

MixColumns() - смешивание столбцов (вносит рассеивание в шифр)
каждый столбец рассматривается как полином 4-ой степени:
S(x)=S0c+ S1cX+ S2cX2+ S3cX3
a(x) - константа
из лекций:

AddRoundKey()
каждый RoundKey такого же размера, что и State. Процедура производит побитовый XOR каждого байта State с каждым байтом RoundKey.

Шифрование:


В заключении сформулируем основные особенности AES:
новая архитектура «Квадрат», обеспечивающая быстрое рассеивание и перемеши вание информации, при этом за один раунд преобразованию подвергается весь входной блок;
байт-ориентированная структура, удобная для реализация на 8-разрядных микро контроллерах;
• все раундовые преобразования суть операции в конечных полях, допускающие эффективную аппаратную и программную реализацию на различных платформах
Вопрос 31. Простое число. Количество простых чисел. Основная теорема арифметики.
Простое число — это натуральное число, имеющее ровно два различных натуральных делителя: единицу и само себя.
Простых чисел бесконечно много. Самое старое известное доказательство этого факта было дано Евклидом в «Началах» (книга IX, утверждение 20). Его доказательство может быть кратко воспроизведено так:
Представим, что количество простых чисел конечно. Перемножим их и прибавим единицу. Полученное число не делится ни на одно из конечного набора простых чисел, потому что остаток от деления на любое из них даёт единицу. Значит, число должно делиться на некоторое простое число, не включённое в этот набор. Противоречие.
|
|
|

Основная теорема арифметики:
Каждое натуральное число  можно представить в виде
можно представить в виде 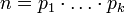 , где
, где  — простые числа, причём такое представление единственно с точностью до порядка следования сомножителей.
— простые числа, причём такое представление единственно с точностью до порядка следования сомножителей.

|
|
|


