Обобщенный закон Ома для произвольного участка цепи

Структура электрической цепи.

Структура электрических цепей это соединения элементов определенным способом, и она не зависит от типа элементов. Поэтому структуру можно изучать по абстрактным графическим схемам цепи, на которых не отображается тип элементов. Такие схемы называют графами электрических цепей.

3. Граф и матрица электрической цепи:

Условное изображение схемы, в котором каждая ветвь заменяется отрезком линии, называется графом электрической цепи. При этом следует помнить, что ветви могут состоять из каких-либо элементов, в свою очередь соединенных различным образом.

Отрезок линии, соответствующий ветви схемы, называется ветвью графа. Граничные точки ветви графа называют узлами графа. Ветвям графа может быть дана определенная ориентация, указанная стрелкой. Граф, у которого все ветви ориентированы, называется ориентированным.

Матрица (используются также другие названия этой матрицы: полная матрица инциденций, матрица соединений, структурная матрица) – это таблица, в которой число столбцов равно числу ветвей графа p, а число строк равно числу узлов q. Номера строк совпадают с номерами узлов (строка с нулевым номером обычно располагается последней), номера столбцов совпадают с номерами ветвей. Элемент матрицы aij, расположенный на пересечении i-й строки и j-го столбца, может принимать значения +1, -1 и 0: aij = 1, если ветвь j инцидентна узлу i и направлена от этого узла; aij = -1, если ветвь j инцидентна узлу i и направлена к этому узлу; aij = 0, если ветвь j не инцидентна узлу i.

4. Законы Кирхгофа:

Cумма токов, подходящих к узловой точке электрической цепи, равна сумме токов, уходящих от этого узла.

В замкнутом контуре электрической цепи сумма всех ЭДС равна сумме падения напряжения в сопротивлениях того же контура.

E1 + E2 + E3 +...+ En = I1R1 + I2R2 + I3R3 +...+ InRn.

5. Эквивалентные преобразования последовательного параллельного и смешанного соединения потребителей:

При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит один и тот же ток I.

R=R1+R2

При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви.Заменяя схемы параллельного соединения приемников лампы резисторами с сопротивлениями R1, R2, R3 При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи

R=R1*R2/(R1+R2)

 

Обобщенный закон Ома для произвольного участка цепи

IR = U12 = φ1 – φ2 + E

Где Е - ЭДС

Произведение силы тока на сопротивление участка цепи равно алгебраической сумме падения потенциала на этом участке и ЭДС всех источников электрической энергии, включенных на данным участке цепи.

8 Баланс мощностей:

В любой электрической цепи должен соблюдаться энергетический баланс - баланс мощностей: алгебраическая сумма мощностей всех источников равна арифметической сумме мощностей всех приемников энергии.

6. Эквивалентные преобразования соединения потребителей звездой и треугольником.

Звезда->Треугольник: Треугольник - > Звезда:

9. Расчет неразветвленных цепей.

Простейш неразветвленная цепь:

I=E/R

P=E*I

10. Расчет разветвленных цепей с одним источником.

R _ЭКВ = R ₁ + R _{2, 3} + R ₄

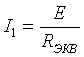U _аб = R _{2, 3}· I ₁

Р _И = Е·I ₁

11. Метод уравнений Кирхгофа.

Рисунок для заданий 11-13:

Первый закон Кирхгофа: в узле электрической цепи алгебраическая сумма токов равна нулю.

 

Второй закон Кирхгофа: в замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех сопротивлениях контура.

Эти системы дают достаточное количество уравнений для отыскания всех неизвестных токов.

 

12. Метод контурных токов.

 

Составляется системы уравнений по второму закону кирхгофа для контурных токов в каждом контуре:

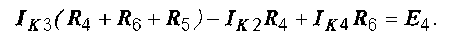
После решения системы действительные токи ветвей определяются по найденным контурным:

13. Метод узловых потенциалов.

Уравнения, составляемые по этому методу, называются узловыми уравнениями. В качестве неизвестных они содержат потенциалы узлов, причем один из них задается заранее – обычно принимается равным нулю.

Запишем для каждой ветви выражение закона Ома:

Подставляем эти токи в систему:

И получим n-1 уравнений (n-число узлов):

14. Метод наложения.

ток в любой ветви сложной электрической цепи, содержащей несколько ЭДС, может быть найден как алгебраическая сумма токов в этой ветви от действия каждой ЭДС в отдельности.

15. Метод эквивалентного источника напряжения.

Нужно рассчитать ток I3:

Р е ш е н и е.

а) Расчет режима холостого хода.

Убираем третью ветвь, оставляя зажимы m и n разомкнутыми (рис. 1.21, а). Напряжение между ними, равное U_X, находится как падение напряжения на сопротивлении R2:

б) Расчет режима короткого замыкания. Замыкаем накоротко зажимы m и n (рис. 1.21, б). Ток короткого замыкания:

Ik=E1/R1=75 (A)

Внутреннее сопротивление эквивалентного генератора:

Rэ=Ux/Ik

16. Цепи синусоидального тока. Основные характеристики гармонических сигналов. (3.1)

Период

Частота . (3.2)

Также существует понятие угловой (циклической) частоты:

. (3.3)

синусоидального тока и напряжения.

, (3.4)

где – мгновенное значение;

– амплитуда переменного сигнала – максимальная по модулю его величина;

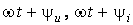– фаза гармонического сигнала – аргумент при синусе в каждый момент времени;

– начальная фаза – значение аргумента в начальный момент времени (t = 0). Фаза измеряется в радианах или градусах.

действующим значением тока:

 

. (3.8)

. (3.9)

Мгновенная мощность

Средняя мощность за период называется активной мощностью:

. (3.11)

17. Цепи синусоидального тока. Гармонический ток в сопротивлении.

Если напряжение u = Um sin(ωt + y) подвести к сопротивлению R, то через сопротивление пройдет гармонический ток

.

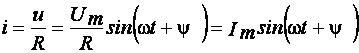напряжение на зажимах сопротивления и ток, проходящий через это сопротивление, имеют одинаковую начальную фазу,

18. Цепи синусоидального тока. Гармонический ток в индуктивности.

напряжение на емкости C синусоидально u = Umsin(wt+y).

Электродвижущая сила самоиндукции определяется по формуле

(1.3)

. Значит, напряжение на индуктивности

.

19. Цепи синусоидального тока. Гармонический ток в емкости.

 

ток i опережает приложенное напряжение и на угол π/2

20. Цепи синусоидального тока. Последовательное соединение R, L, C.

 

Для мгновенных значений токов и напряжений выполняются I и II законы Кирхгофа.

При прохождении синусоидаль­ного тока 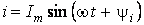через электрическую цепь, состоящую из последовательно соединенных элементов R, L, C (рис. 3.9), на выводах a – b этой цепи создается синусоидальное напряжение, равное по IIзакону Кирхгофа алгебраической сумме синусоидальных напряжений на отдельных элементах:

 

(3.21)

– цепь носит чисто активный характер

– цепь носит индуктивный характер, т.е. ;

– цепь носит емкостный характер, т.е. .

Полное сопротивление цепи

;

угол разности фаз

,

(3.24)

что удобно представлять с помощью треугольника сопротивлений (рис. 3.10).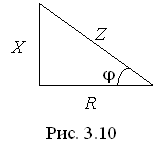

Умножив левые и правые части выражений для сопротивлений (3.24) на действующее значение тока I, получим соответственно действующие значения напряжений на активном и реактивном сопротивлениях, которые называют активной и реактивной составляющими напряжения:

(3.25)

Тогда действующее значение суммарного напряжения можно определить как Для напряжений также можно построить прямоугольный треугольник напряжений.

 

21. Цепи синусоидального тока. Параллельное соединение R, L, C.

Если к выводам электрической цепи, состоящей из параллельно соединенных R, L, C приложено синусоидальное напряжение то по I закону Кирхгофа синусоидальный ток в неразветвленной части равен алгебраической сумме синусоидальных токов в параллельных ветвях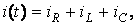

Активная проводимость цепи , всегда положительна.

Реактивная проводимость цепи , в зависимости от знака может иметь индуктивный (В > 0)или емкостный (B < 0)характер. Если В = 0, цепь носит активный характер.

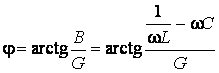– угол разности фаз определяется по оси в направлении от напряжения к току и является острым или прямым .

– при индуктивном характере цепи, т.е. при B > 0; при этом ток опережает по фазе напряжение.

– при емкостном характере цепи, т.е. при B < 0; при этом ток опережает по фазе напряжение.

– при резистивном характере цепи, т.е. при равенстве

22. …

 

23.Символический метод расчета. Законы Ома и Кирхгофа.

Закон Ома:

Пусть мгновенные значения напряжения и тока на зажимах произвольного пассивного двухполюсника определяются выражениями, комплексы действующих значений которых соответственно равны:

а их отношение определяет комплексное сопротивление двухполюсника:

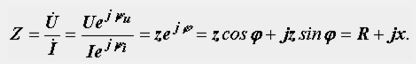
Величина, обратная комплексному сопротивлению – комплексная проводимость:

Сопротивления z, R, x и проводимости y, G и B, входящие в два последних выражения, есть не что иное, как эквивалентные параметры двухполюсника.

 

 

24. Символический метод расчета. Последовательное соединение R, L, C.

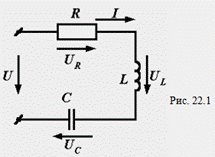
Величины напряжений на отдельных элементах цепи:

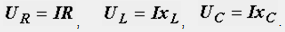
Из треугольника oab по теореме Пифагора находим:

Вынося из под знака радикала, записываем последнее выражение в виде: U=I*z; где,z - полное сопротивление.

В последней формуле разность индуктивного и емкостного сопротивлений мы обозначили буквой х. Это общее реактивное сопротивление цепи: х = х_L – x_C.

Выражение U=Iz называется законом Ома для всей цепи. Оно может быть записано и так: I=U/z=Uy.

где, y– полная проводимость цепи, представляющая величину, обратную полному сопротивлению 1/z

Если необходимо определить угол сдвига фаз между напряжением и током, то это можно сделать из треугольника напряжений oab

 

25. Символический метод расчета. Параллельное соединение R, L, C.

Рассмотрим схему, состоящую из параллельно соединенных активного и реактивных элементов.

Требуется по известным G, В_L, В_C, U рассчитать токи

 

Подставив в уравнение первого закона Кирхгофа, получаем:

 

 

Поделиться:

Воспользуйтесь поиском по сайту: