 |
Составьте математическое описание ИДПТЯУ в виде ДУ нормальной формы (иначе, в уравнениях состояния), опираясь на уравнения для якорной цепи, моментов, ЭДС и электромагнитного момента.
|
|
|
|
Какие параметры выходного сопротивления УВ, подключенного к якорной цепи ИДПТ, и как влияют на электромеханическую постоянную времени комплекса “УВ-ИДПТ”?
Электромеханическая постоянная времени 
задаётся соотношением:
,
где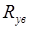 
- активное выходное сопротивление УВ; 
- активное сопротивление якорной обмотки;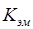 
- электромеханический коэффициент.
Таким образом, электромеханическая постоянная времени увеличивается при увеличении сопротивления .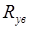
Какие параметры выходного сопротивления УВ, подключенного к якорной цепи ИДПТ, и как влияют на электромагнитную постоянную времени комплекса “УВ-ИДПТ”?
Электромагнитная постоянная времени 
задаётся соотношением:
,
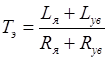где 
, 
- индуктивности якорной обмотки и выходного сопротивления 
. При увеличении сопротивления 
и уменьшении индуктивности электромагнитная постоянная уменьшается.
Какие параметры ДУ для угловой скорости вращения ИДПТЯУ, выведенного в п.2.31, определяют время регулирования данной скорости при ступенчатом изменении якорного напряжения?
Время регулирования определяется электромеханической постоянной времени .
Запишите ДУ для угловой скорости вращения ИДПТЯУ при условии, что электромагнитная постоянная времени много меньше электромеханической. Запишите решение этого ДУ при ступенчатом изменении якорного напряжения и постройте график изменения угловой скорости вращения. К какому типу кривых относится данный график?
Искомое ДУ следует из ДУ(10), выведенного в вопросе 2.31 для произвольных значений электромагнитной и электромеханической постоянных времени. В данном случае принимаем, что 
, поскольку по условию 
. Тогда указанное уравнение (10) принимает вид:
|
|
|
. (1)
Решая ДУ(1), при условии, что якорное напряжение 
изменяется ступенчато и принимает при 
< 0 значение 
, получим:
Рис.2.37.1
|
, (2)
где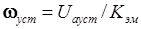 
.
Уравнению (2) соответствует график, приведенный на рис. 2.37.1.
Указанный график, именуется экспонентой.
Рис.2.38.1
|
Как графоаналитически может быть определена электромеханическая постоянная времени ИДПТ при условии, что она много больше электромагнитной постоянной времени?
Графоаналитическое определение электромеханической постоянной времени 
(рис. 2.38.1): если провести касательную к экспоненте в точке 
, то отрезок отсекаемый на уровне 
равен в масштабе времени величине . Здесь: 
- момент сопротивления на валу.
Как определяется время регулирования частоты вращения либо угловой скорости вращения ИДПТЯУ при условии, что электромагнитная постоянная времени много меньше электромеханической?
Время регулирования 
определяется из соотношения: 
, где - электромеханическая постоянная времени.
Какие значения принимают электромеханические постоянные времени ИДПТ мощностью до нескольких десятков ватт?
Электромеханические постоянные времени ИДПТ определяется конструкцией якоря и имеют следующие значения:
– для якоря обычного типа 
;
– для полого и беспазового якорей 
;
– для дискового якоря и якоря с печатной обмоткой 
.
Составьте математическое описание ИДПТЯУ в виде ДУ нормальной формы (иначе, в уравнениях состояния), опираясь на уравнения для якорной цепи, моментов, ЭДС и электромагнитного момента.
По второму закону Кирхгофа для якорной цепи можно записать уравнение (1). Здесь: 
- якорное напряжение и ток якорной обмотки; Е – ЭДС якорной обмотки (или противоЭДС двигателя); 
- активное сопротивление и индуктивность якорной обмотки. На валу двигателя будем полагать действует электромагнитный момент М и противодействующие ему момент сопротивления нагрузки 
и динамический момент 
, где J – момент инерции якоря; 
- угловая скорость вращения якоря. Эти моменты уравновешены в любой момент времени, что математически записывают уравнением равновесия моментов (2). Известно, что ЭДС Е и электромагнитный момент М машины постоянного тока задаются соотношениями (3) и (4). Здесь: 
- электромагнитный коэффициент.
|
|
|
Для получения уравнений состояния двигателя необходимо систему уравнений (1) – (4) преобразовать так, чтобы все производные были бы выражены явно, то есть в левой части преобразованной системы уравнений остались бы только производные, а в правой величины, не содержащее производных. Результат указанных преобразований от исходной системы уравнений к уравнениям состояния представляем системой (5),(6).
Уравнения состояния (5),(6), как это нетрудно показать, могут быть представлены в матричной форме соотношением (7).
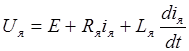, (1)
, (2)
, (3)
. (4)
. (5)
(6)
(7)
2.41а Составьте математическое описание ИДПТЯУ в операторном виде.
|
|
|
