Задачи для самостоятельного решения в аудитории и на дом

 

Задание по изучения теории дома. Готовиться к проверочной работе. Учить лекцию "Системы координат"

1. Вычислить объем и высоту DH тетраэдра ABCD:

1) A (2,-1,1), B (5,5,4), C (3,2,-1), D (4,1,3); 2) A (2,3,1), B (4,1,-2), C (6,3,7), D (-5,-4,8).

2. Найти площадь треугольника ABC и длину высоты BH: 1) A (1,2,0), B (3,0,-3), C (5,2,6); 2) A (1,-1,2), B (5,-6,2), C (1,3,-1).

3. Дан параллелограмм ABCD.  Прямая l пересекает прямые AB, AC, AD в точках B’, C’, D’ и Докажите, что .

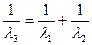4. На прямых BC, CA,AB определяющих треугольник ABC взяты точки L,M, N,лежащие на одной прямой. Докажите, что если 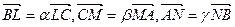, то abg=-1 (теорема Менелая).

5. Точка пересечения средних линий четырехугольника совпадает с точкой пересечения его диагоналей, доказать, что четырехугольник - параллелограмм.

6. Докажите, что средины сторон произвольного четырехугольника являются вершинами параллелограмма.

7. В треугольника ABC на сторонах AB, BC взяты соответственно точки K, L, так что AK:BK=1:2, CL:BL=2:1, Q точка пересечения прямых AL и CK. Площадь треугольника BQC равна 1. Найти площадь треугольника ABC.

8. Точка К делит медиану AD треугольника ABC в отношении 3:1, считая от вершины.. В каком отношении прямая делит площадь треугольника ABC/

9. На каждой медиане треугольника взята точка, делящая ее как 3:1, считая от вершины. Найти отношение площади треугольника с вершинами вэ тих точках к площади исходного треугольника.

10. Пусть на ребрах DA, DB, DC тетраэдра ABCD отложены соответственно точки M, N, P так что DM=k₁DA, DN=k₂DB, DP=k₃DB.  Доказать, что объем тетраэдраMNPD равен k₁k₂k₃V.

11. Дана правильная четырехугольная пирамида SABCD. Через середины ребер AB, AD, CS проведена плоскость, в каком отношении эта плоскость делит объем пирамиды.

12. В треугольнике ABC длины сторон a,b,c. Найти длину Высоты AH,длину медианы AM, длину биссектрисы AE.

13. Для треугольника ABC доказать неравенства

1) cos 2A +cos 2B + cos 2C >-3/2;

2) cos A +cos B + cos C £3/2;

3) sin²A +sin²B + sin²C£9/4.

14. Доказать, что центр описанной окружности O, центр тяжести G ортоцентр H произвольного треугольника принадлежат одной прямой (прямой Эйлера) и |OG|:|GH|=1:2.

15. Дан произвольный тетраэдр ABCD. Докажите, что  .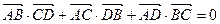

16. Докажите, что если в тетраэдре две пары противоположных ребер перпендикулярны, то и третья пара противоположных ребер перпендикулярна.

17. Докажите, что суммы квадратов противоположных ребер тетраэдра равны тогда и только тогда, когда третья пара противоположных ребер перпендикулярна.

18. Два правильных пятиугольниках OABCD и OA’B’C’D’ c общей вершиной О не лежат в одной плоскости. Докажите, что прямые AA’, BB’, CC’, DD’ параллельны одной плоскости.

19. Из точки О, лежащей внутри выпуклого многогранника, проведены лучи перпендикулярные плоскостям граней и пересекающие их. На этих лучах от точки О отложены векторы, длины которых равны площадям соответствующих граней. Докажите, что сумма этих векторов равна нулю.

20. Докажите, что в параллелепипеде ABCDA’B’C’D’ сумма квадратов терех непараллельных граней равна сумме квадратов площадей граней тетраэдра A’BC’D.

21. Дан тетраэдр и точка N. Через каждое ребро тетраэдра проведена плоскость, параллельная отрезу, соединяющую точку N с серединой противоположного ребра. Докажите, что все шесть этих плоскостей пересекаются в одной точке.

22. Через середину каждого ребра тетраэдра проведена плоскость, перпендикулярная противоположному ребру, соединяющую точку N с серединой противоположного ребра. Докажите, что все шесть этих плоскостей пересекаются в одной точке (точка Монжа).

Литература.

Просолов В.В. Задачи по стереометрии.: Наука, 1989.

Цыпкин А.Г., Пинский А.И. Справочник по методам решения задач по математике для средней школы. М.:Наука, 1989.

Ответы и указания к решению задач:

1.  3, ; 2) 154/3, 11. 2. 1) 14, ;2) 25/2, 5. Указание. Записать условие принадлежности точек A’,B’,C’ прямой, например, в виде 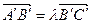. Выразить, входящие сюда, векторы через базисные, например, через .Записать указанное равенство в координатной форме и исключить параметр l. 4. Указание. См. Указание к задаче 3.

Поделиться:

Воспользуйтесь поиском по сайту: