 |
Метод Фурье-оптики измерения параметров капилляров
|
|
|
|
Основные принципы Фурье-оптики основаны па том, что оптическая система хорошего качества является элементом, осуществляющим преобразование Фурье. Т.е. в плоскости изображения оптической системы наблюдается дифракционная картина, математически являющаяся преобразованием Фурье от поля в предметной плоскости. Кратко поясним это.
Пусть предмет с амплитудным коэффициентом пропускания 
расположен непосредственно перед линзой и направим на него плоскую монохроматическую волну. На плоскости перед линзой образуется поле 
, где 
- амплитуда плоской волны. Поле на выходе линзы с фокусным расстоянием 
определяется функцией:
Конечный размер апертуры линзы или объектива учитывается функцией зрачка 
, которая равна 1 внутри световой апертуры и равна нулю вне световой апертуры.
Тогда дифракционная картина в фокальной плоскости линзы описывается формулой дифракции Френеля:
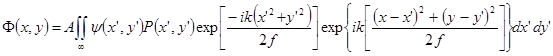
После элементарных преобразований формула принимает вид:
Отсюда видно, что распределение амплитуд о фокальной плоскости с точностью до несущественных для дифракционной картины фазовых и масштабных множителей является Фурье-образом распределения амплитуд на входе оптической системы. Таким образом, оптическая система является элементом, осуществляющим преобразование Фурье.
В случае произвольного расположения плоскости предмета процесс дифракционного преобразования изображения сводится к двум стадиям:
формированию в фокальной плоскости ОС дифракционной картины предмета;
преобразованию дифракционной картины предмета в фокальной плоскости ОС в изображение предмета в плоскости изображений.
Все параметры, характеризующие предмет, представлены в дифракционном распределении интенсивности в фокальной плоскости линзы и могут быть определены по этому распределению однозначно.
|
|
|
С математической точки зрения это соответствует однозначному восстановлению функции по ее Фурье-образу.
Если произвести в фокальной плоскости изменения дифракционной картины (например, закрыть или, наоборот, усилить некоторые максимумы), то произойдет соответствующее изменение поля в плоскости изображении предмета. Внесение изменений в изображение предмета посредством модификации в фокальной плоскости ОС дифракционной картины, из которой в последующем формируется изображение, называется пространственной фильтрацией изображения.
При использовании принципов пространственной фильтрации необходимо производить расчеты дифракционного распределения поля в фокальной плоскости ОС.
Микроскопический метод
Обобщенная оптическая схема определения параметров отверстия фильеры представлена на рис. 9. Источник света 1 освещает отверстие фильеры 3, находящейся на предметном столике микроскопа 2. Объектив 4 микроскопа строит изображение отверстия с необходимым увеличением в плоскости пространственно-чувствительного приемника - ПЗС матрицы 8, сигнал с которой может быть направлен на видеоконтрольное устройство 11 через электронный блок сопряжения 12, на ПЭВМ. Для визуального наблюдения отверстия и получения фотодокумента в ход лучей вводится поворотное зеркало 5. В одном положении зеркала изображение отверстия строится в плоскости сетки 6 и наблюдается в окуляр 7, в другом - через оптический элемент сопряжения 10 регистрируется фотоприставкой 9.
Рассмотрим возможности оптической системы при визуальном наблюдении и фотоэлектрической регистрации. Будем предполагать, что приемником излучения является ПЗС матрица размером 576x798 элементов, отверстие фильеры круглое с диаметром 
и высотой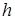 
, т.е. отношение высоты 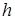к диаметру 
известно. Предположим далее, что выбором увеличения 
объектива в изображении отверстия на диаметре укладывается N = 500 элементов ПЗС - матрицы (т.е. размер изображения 
в зависимости от размера пикселя). Это означает, что при визуальном наблюдении отверстие занимает примерно половину поля зрения окуляра. Легко показать, что при этих условиях разрешение микроскопа как при визуальном (при наблюдении глазом через окуляр), так и при фотоэлектрическом (при проецировании на ФПУ) методе измерения практически всегда будет определяться дифракционным пределом разрешения объектива
|
|
|
, где
- числовая апертура объектива,
- длина волны света.
Действительно, предположим обратное, тогда геометрический предел разрешения, обусловленный конечным размером пикселя ПЗС матрицы 
больше дифракционного, т.е. 
.
Отсюда последовательно получим:
.
Для реальных микрообъективов
, тогда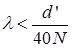 
.
При 
, N = 500 получим 
, а для видимой области 
, поэтому пределом разрешения будет .
Оценим теперь глубину резкого изображения при визуальном и фотоэлектрическом наблюдении. Как известно, при визуальном наблюдении общая глубина резкого изображения 
складывается из трех составляющих: геометрической 
, волновой 
и аккомодационной 
, где
- видимое увеличение микроскопа,
- угловое разрешение глаза, 
- показатель преломления среды в плоскости наблюдения ( = 1).
Полагая, что при визуальном наблюдении увеличение микроскопа соответствует нормальному Г = 500А получим:
[мкм], 
[мкм], 
[мкм].
Следовательно, для = 0,5 мкм получим:
[мкм].
При визуальной регистрации входной и выходной плоскостей целесообразно исключить влияние 
. Это достигается на практике тем, что фильера наблюдается одновременно с резким изображением сетки. Тогда
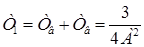[мкм].
При фотоэлектрической регистрации величина 
сохраняется, а значение 
следует определять выражением:
где 
- геометрический предел разрешения в плоскости ПЗС матрицы (
).
Для реальных объективов 
, причем большее значение соответствует более светосильным объективам. С учетом этого получим 
[мкм]. Общая глубина резкого изображения при фотоэлектрической регистрации составит:
|
|
|
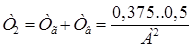[мкм].
Здесь также принято 
= 0,5 мкм.
Для оценки можно принять большее значение полученного выражения, т.е. окончательно для фотоэлектрической регистрации получим:
Из изложенного следует, что для более точной регистрации глубины отверстия фильеры необходимо, по возможности, использовать более светосильные объективы. Кроме того, видно, что фотоэлектрическая регистрация глубины отверстия обладает некоторым преимуществом по сравнению с визуальной.
Оценим погрешность фотоэлектрического метода определения глубины отверстия для двух значений диаметров фильеры 
и 
. Полагая в обоих случаях 
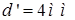, получим 
и 
. Для первого объектива числовая апертура 
, для второго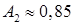 
. Следовательно, для первого отверстия 
, 
; для второго отверстия 
, 
. Таким образом, погрешность измерения глубины отверстия не превышает 0,02 мм для диаметра 0,5 мм и 0,001 мм для диаметра 0,05 мм.
Исходя из изложенного, можно предложить следующую схему автоматизированного фотоэлектрического контроля отверстий фильеры с использованием ПЭВМ. Сущность этой схемы иллюстрируется рис. 1,2. Фильера имеет возможность горизонтального перемещения по столику в двух взаимно перпендикулярных направлениях (В). Это перемещение осуществляется, например, шаговыми двигателями, управляемыми ПЭВМ. Поскольку положения отверстий фильеры известны, то программным путем можно точно выставить каждое отверстие в центр поля зрения микроскопа. Предметный стол микроскопа имеет возможность точного перемещения по глубине (стрелка С). Смещая программным путем столик по стрелке С с шагом 
, равным глубине резкости, можно записать ряд дискретных изображений по глубине отверстия в ПЭВМ. В каждом из этих изображений резко будут представлены элементы отверстия, находящиеся внутри соответствующей области (рис. 2а). Если затем программным путем определить для каждой из областей необходимый масштаб и последовательно «сложить» на плоскости все области так, чтобы обеспечивалась непрерывность перехода из одной области в другую, то получим плоскую развертку цилиндрической поверхности отверстия (рис. 2в). На рис. 2 показано, как при таком методе на развертке будут изображаться включения 1,2,3. Оценить размеры включений и их конфигурацию можно программным путем из анализа записанных дискретных изображений.
|
|
|
Для реализации предлагаемой схемы необходимо приобретение следующего оборудования:
универсального микроскопа с шаговым приводом стола с точностью перемещения 
;
ПЗС камеры типа ТСД 5120 АД;
видеоконтрольного устройства сопряжения ПЗС-камеры с ПЭВМ;
ПЭВМ класса PII.
Кроме того, необходима разработка электронных плат сопряжения и программного обеспечения.
Моделирование указанной схемы с помощью микроскопа визуальным методом показало, что реализация предлагаемого метода контроля возможна. Указанные в ТЗ точностные параметры достижимы, особенно если применить ряд мер, направленных на повышение контраста изображения (например, использование поляризатора в осветителе и анализатора в микроскопе).
Для апробации и иллюстрации предлагаемого метода контроля были проведены экспериментальные исследования отверстия фильеры диаметром 
и глубиной 
. Измерительная установка в целом соответствовала обобщенной схеме (рис. 9), однако ее технические параметры значительно отличались от оптимальных. В частности, рабочее число элементов ПЗС матрицы составляло 
, а в качестве объектива использовался микрообъектив с параметрами 
, 
. Для обеспечения необходимого увеличения между объективом и ПЗС матрицей устанавливалась дополнительная линза.
На рис. 11 представлены 9 дискретных изображений по глубине отверстия с шагом 
. Из последнего изображения, кстати, видно, что нижняя граница отверстия фильеры не горизонтальна (правый край резкий, а левый размыт). Эти изображения были обработаны вручную по описанной выше схеме с помощью прикладного пакета обработки изображений Adobe Photoshop 5.0. Полученная при этом развертка отверстия фильеры представлена на рис. 4. Подчеркнем, что материалы на рис. 11 и рис. 12 носят в основном иллюстративный, нежели метрологический характер, т.к. предел разрешения и глубина резкого изображения установки были значительно больше оптимальных. Тем не менее, из них хорошо видно наличие, расположение и характер дефектов отверстия.
|
|
|
