Научный руководитель Богатов Егор Михайлович, ввести специфику

Интегрирование при подготовке специалистов по направлению автоматизации информационных технологий

Фомин Антон Александрович, студент 1-ого курса

Научный руководитель Богатов Егор Михайлович, ввести специфику

Федеральное государственное автономное образовательное учреждение высшего образования «Национальный исследовательский технологический университет «МИСиС» Старооскольский технологический институт им. А.А. Угарова (филиал) федерального государственного автономного образовательного учреждения высшего образования «Национальный исследовательский технологический университет «МИСиС»,

Г. Старый Оскол

 

Цель исследования: выявить актуальность использования приёма интегрирования в жизни.

Задача исследования: показать практическое применение теоретического материала по теме применение интегрирования в жизни.

Метод исследования: анализ научной литературы и использование источник из сети интерент.

Рассмотрим самое простейшее применение интеграла в жизни. Каждый день мы работает или учимся, какое-то определенное число часов, а также соответственно выполняем определенный объём работы. Исходя из этого можно обозначить время начала работы постоянной , а время окончания работы постоянной . Объём выполненной работы обозначим функций . Отсюда следует, что наша выполняемая работа является определенным интегралом . Далее перейдем к актуальным примерам, которые изучают студенты при подготовке по направлению автоматизации информационных технологий.

Физика: Каждый из нас знает, что тело в пространстве каким-либо образом движется. Если представить ситуацию, что человек, идёт по прямой и проходит путь за определенное время. Используя простейший пример, описанный ранее, можно обозначить время теми же величина, но функция уже будет скоростью, которая изменяется по закону . Исходя из этого, можно найти путь пройденный человеком который будет равен определённому интегралу .

Рассмотри задачу для нахождения количества выделенной теплоты за определнный промежуток времени. Если задана телпоемкость , на произвольном промежутке времени, то получим уравнение .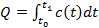

Теперь немного отвлечемся и узнаем историческое применение интеграла.

Если бы бочки умели говорить, то, несо­мненно, многие из них с удовольствием рас­сказали бы поучительную историю о великих заслугах бочек в создании высшей матема­тики.

В ноябре 1613 г. королевский математик и астролог австрийского двора И. Кеплер праздновал свадьбу. Готовясь к ней, он при­обрел несколько бочек виноградного вина. При покупке Кеплер был поражен тем, что про­давец определял вместимость бочки, производя одно-единственное действие — измеряя рас­стояние от наливного отверстия до самой даль­ней от него точки днища. Ведь такое измерение совсем не учитывало форму бочки! Кеплер сразу увидел, что перед ним интерес­нейшая математическая задача — по нескольким измерениям вычислить вместимость бочки. Размышляя над этой задачей, он нашел фор­мулы не только для объема бочек, но и для объема самых различных тел: лимона, яб­лока, айвы и даже турецкой чалмы. Для каждого из тел Кеплеру приходилось создавать новые, зачастую очень хитроум­ные методы.

В наши дни вычислять объемы различных тел (значительно более сложных, чем у Кепле­ра) необходимо при решении многих техни­ческих задач: при нахождении объема корпуса корабля, объема газгольдера, объема водохра­нилища и др. И решать такие задачи приходится почти каждому инженеру, каждому тех­нику. Простые и общие методы решения по­добных задач даются высшей математикой.

Математика:

Рассмотрим задачу об определении площади криволинейной трапеции ограниченной сверху функцией , снизу отрезком оси , и по краям вертикальными прямыми x=a, x=b.

Разобъем трапецию вертинкальными прямыми проходящими через точки .

 

Тогда ее площадь равна суме площадей и полосок, что эквивалентно

Допустим, нам придётся найти объём колеса, которое установлено на вашу машину, но данные о нем затерлись в следствии времени. Для этого обратимся к вычислению объема тела вращения. Представим, что колесо — это цилиндр, с вырезанной окружностью, находящейся в центре, с определнным радиусом.

 

 

http://enciklopediya1.ru/index/0-474

http://ru.solverbook.com/spravochnik/integraly/primenenie-integralov-v-fizike-matematike/

 

Поделиться:

Воспользуйтесь поиском по сайту: