 |
Понятие о гармонических токе и напряжении
|
|
|
|
Лабораторная работа №1 «Исследование простых электрических цепей в установившемся гармоническом режиме»
Цель работы: Измерение гармонических напряжений и фазовых соотношений между ними в простейших цепях, сопоставление результатов эксперимента с результатами расчета и теоретическими положениями.
Краткие теоретические сведения
Понятие о гармонических токе и напряжении
Особое место среди различных физических процессов занимают так называемые периодические процессы. Данный интерес вызван их широким распространением среди физических явлений: движение планет вокруг солнца, суточное вращение Земли, механические колебания математического или физического маятника и пр. Под периодическими будем понимать такие процессы, для которых значения физической величины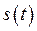 
их характеризующей повторяются через определенный промежуток времени 
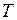, называемый периодом.
Для того чтобы считать процесс периодическим, необходимо, чтобы наблюдение за ним проводилось на протяжении достаточно большого промежутка времени, теоретически бесконечно большого. Таким образом, мгновенные значения физической величины будут повторяться через различные промежутки времени, кратные периоду:
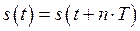, где 
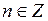. (1.1)
А, значит, под периодом следует понимать минимальный интервал времени, через который мгновенные значения физической величины повторяются в той же последовательности. Иначе говоря это время одного полного колебания.
Одним из простейших видов периодических процессов являются так называемые гармонические колебания, при которых мгновенные значения физической величины изменяются по гармоническому закону, то есть по закону синуса или косинуса. При изучении линейных электрических цепей процессы в них принято характеризовать мгновенными значениями тока 
и напряжения 
. Таким образом, мгновенные значения этих физических величин определяются выражениями:
|
|
|
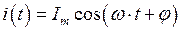, (1.2)
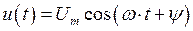, (1.3)
где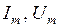 
- амплитуды колебаний тока и напряжения, 
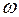- угловая частота, а 
- начальные фазы. Поясним физический смысл введенных числовых параметров гармонических колебаний на примере графического представления (рис. 1.1).
Рис. 1.1 - Графическое представление гармонического напряжения
Из графика гармонического напряжения видно, что амплитуда – это наибольшее из мгновенных значений, принимаемых гармоническим напряжением за время одного периода.
В зависимости от значения своего аргумента косинус, определяющий мгновенное значение гармонического тока или напряжения, может принимать значения в диапазоне от -1 (аргумент равен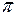 
радиан, или 
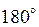) до 1 (аргумент равен нулю), причем значения косинуса повторяются в той же последовательности через интервалы времени, кратные 
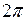радиан или 
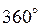. Иными словами, аргумент косинуса определяет стадию развития колебания и носит название полной фазы колебания:
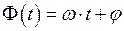или 
. (1.4)
Как показывают выражения (1.4) полная фаза с течением времени линейно нарастает. Скорость изменения полной фазы колебания носит название угловой частоты :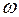
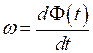или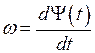 
, (1.5)
а ее значение в момент времени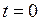 
- начальной фазы 
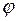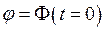(или 
):
или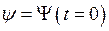 
. (1.6)
В отличие от полной фазы колебания, начальная фаза может принимать значения аргумента косинуса, соответствующие одному периоду его изменения. Принято полагать, что эти значения заключены в интервале от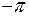 
до 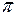радиан (от 
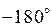до ).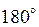
Из рис. 1.1 видно, что стадия развития колебания в начальный момент времени (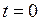) определяется величиной смещения 
графика косинуса по оси времени:
. (1.7)
Таким образом, если график гармонического напряжения смещен против направления временной оси, как показано на рис. 1.1, то начальная фаза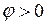 
, а при его смещении вдоль направления - начальная фаза 
.
|
|
|
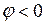Величина угловой частоты связана с периодом колебания:
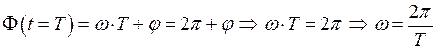(1.8)
и с еще одним числовым параметром гармонического сигнала, который носит название линейной (циклической) частоты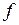 
:
, (1.9)
под которой понимают число колебаний, совершаемых гармоническим током (или напряжением) за единицу времени.
В общем случае, когда закон изменения мгновенной величины не является гармоническим и, вообще говоря, симметричным, физическую величину (в теории электрических цепей это, по-прежнему, ток и напряжение) принято характеризовать усредненными числовыми параметрами:
· среднее за период значение
или 
; (1.10)
· среднеквадратическое значение
или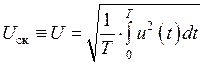 
; (1.11)
· средневыпрямленное значение
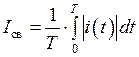или 
. (1.12)
Для гармонических токов и напряжений связь между среднеквадратическим, средневыпрямленным и амплитудным значениями задается соотношениями вида:
или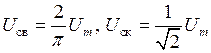 
. (1.13)
При анализе линейных электрических цепей важно не просто определить числовые параметры некоторой реакции (тока или напряжения), но и сравнить их с соответствующими числовыми параметрами другой реакции или воздействия. Однотипные гармонические реакции (имеющие одинаковые размерности единиц измерения), как правило, сравнивают по амплитуде и начальной фазе, считая, что они изменяются с одной и той же частотой (для линейных электрических цепей это условие всегда выполняется). Результатом сравнения двух реакций по амплитуде является вывод: какая из них превосходит какую по амплитуде. Сравнение же двух реакций по начальной фазе осуществляется путем определения, так называемого, фазового сдвига (или сдвига фаз), под которым понимают разность начальных фаз двух гармонических реакций:
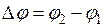или 
. (1.14)
Если сдвиг фаз положителен, то говорят, что вторая из реакций опережает первую по фазе, а если отрицателен – то отстает от нее по фазе. В частных случаях сдвиг фаз может оказаться равным нулю или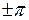 
рад. В первом случае реакции называются синфазными, а во втором – противофазными.
При графическом представлении гармонических колебаний, или их визуальном наблюдении на экране электронного осциллографа, сдвиг фаз между двумя реакциями (например, двумя напряжениями) электрической цепи определяется косвенным способом (рис. 1.2).
|
|
|
Рис. 1.2 - К определению сдвига фаз гармонических напряжений
Если рассмотреть ближайшие моменты времени, в которые обе реакции электрической цепи проходят одну и ту же стадию развития колебания, то их полные фазы окажутся одинаковыми:
, или
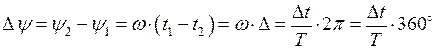. (1.15)
Знак же сдвига фаз определяется следующим образом (см. рис. 1.2):
· если второй сигнал смещен относительно первого вдоль оси времени вправо (рис. 1.2, а), то момент времени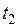 
, в который мгновенное значение данной реакции становится наибольшим, наступает позже соответствующего момента времени 
для первого сигнала, а значит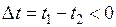 
и сдвиг фаз отрицателен, то есть второе напряжение отстает по фазе от первого;
· если второй сигнал смещен относительно первого вдоль оси времени влево (рис. 1.2, б), то момент времени 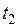, в который мгновенное значение данной реакции становится наибольшим, наступает раньше соответствующего момента времени для первого сигнала, а значит 
и сдвиг фаз положителен, то есть второе напряжение опережает по фазе первое.
|
|
|
