Основное уравнение кинетической теории газов.

Тема 2: ЗАКОНЫ И УРАВНЕНИЯ ИДЕАЛЬНЫХ ГАЗОВ

Лекция 2. Законы идеальных газов.

 

Основное уравнение кинетической теории газов.

Молекулярно-кинетическая теория газов, основываясь на законах движения и взаимодействия молекул, объяс­няет свойства газа и природу теплового движения. Ос­новоположник этой теории Михаил Васильевич Ломо­носов считал, что газ есть совокупность скопления гро­мадного числа мельчайших частичек – молекул, которые при столкновении вступают во взаимодействие по зако­нам упругого удара. Кинетическая теория газов была в дальнейшем развита Клазиусом, Менделеевым, Макс­веллом, Больцманом, Пироговым и др. Теория устанав­ливает следующие положения:

1. строение всех газов дис­кретное, число молекул даже в малом объеме громадно;

2. молекулы идеальных газов представляют собой уп­ругие шарообразные частицы ничтожно малого диамет­ра;

3. между молекулами не проявляются силы взаимодей­ствия;

4. молекулы газа в любом объеме распределяются равномерно и находятся в хаотическом движении;

5. теп­лота есть беспорядочное движение частиц;

6. давление есть совокупность ударов молекул о стенки сосуда.

На осно­вании этих положений и применения законов механики к движущимся молекулам выведено основное уравнение кинетической теории газов, которое имеет вид

или (1)

где р – абсолютное давление идеального газа на стенки сосуда;

п – число молекул в единице объема;

m – масса одной молекулы;

ω – средняя квадратичная скорость поступательного движения мо­лекул;

выражение  определяет среднюю кинетическую энергию поступательного движения одной молекулы.

Согласно основному положению кинетической теории газов, существует связь между средней кинетической энергией молекул газа и его абсолютной температурой:

,

где β –  коэффициент пропорциональности, одинаковый для всех газов.

Подставляя значение  в основное уравнение, получим

,        (2)

т. е. давление прямо пропорционально числу моле­кул в единице объема и абсолютной температуре.

2. Законы Бойля – Мариотта, Гей-Люссака, Шар­ля.

Основные законы идеальных газов используются в технической термодинамике для решения целого ряда инженерно-технических задач в процессе разработки конструкторско-технологическойдокументации авиационной техники, авиадвигателей; их изготовления и эксплуатации.

Эти законы первоначально были получены экспериментальным путем. В последующем они были выведены из молекулярно-кинетической теории строения тел.

Закон Бойля – Мариотта устанавливает зависимость объема идеального газа от давления при постоянной температуре. Эту зависимость вывел английский химик и физик Р. Бойль в 1662 году задолго до появления ки­нетической теории газа. Независимо от Бойля в 1676 го­ду этот же закон открыл Э. Мариотт. Закон Роберта Бойля (1627 – 1691), английского химика и физика, установившего этот закон в 1662 году, и Эдма Мариотта (1620 – 1684),французского физика, установившего этот закон в 1676 году: произведение объёма данной массы идеального газа на его давление постоянно при постоянной температуре или .

Закон получил на­звание Бойля – Мариотта и утверждает, что при посто­янной температуре давление газа обратно пропорцио­нально его объему.

Пусть при постоянной температуре некоторой массы газа имеем:

V ₁– объем газа при давлении р ₁;

V ₂– объем газа при давлении р ₂.

Тогда согласно закону мож­но записать

     (3)

Подставив в это уравнение значение удельного объема и принимая массу данного газа т = 1кг, полу­чим

  (4)

откуда

p ₁ v ₁ = p ₂ v ₂ или p v = const. (5)

 

Плотность газа – величина, обратная его удельному объему:

 

;   

тогда уравнение (4) примет вид

т. е. плотности газов прямо пропорциональны их абсо­лютным давлениям. Уравнение (5) можно рассматривать как новое выражение закона Бойля –  Мариотта которое можно сформулировать так: произведение давления на удельный объем определенной массы одного и того же идеального газа для различных его состояний, но при одинаковой температуре, есть величина постоянная.

Этот закон может быть легко получен из основного уравнения кинетической теории газов. Заме­нив в уравнении (2) число молекул в единице объема отношением N / V (V – объем данной массы газа, N – число молекул в объеме) получим

или       (6)

Поскольку для данной массы газа величины N и β постоянны, то при постоянной температуре T = const для произвольного количества газа уравнение Бойля – Мариотта будет иметь вид

pV = const,              (7)

а для 1 кг газа

p v = const.

Изобразим графически в системе координат р – v из­менение состояния газа.

Например, давление данной массы газа объемом 1 м³ равно 98 кПа, тогда, используя уравнение (7), определим давление газа объемом 2 м³

кПа.

Продолжая расчеты, получим следующие данные: V (м³) равно 1; 2; 3; 4; 5; 6; соответственно р (кПа) равно 98; 49; 32,7; 24,5; 19,6; 16,3. По этим данным строим график (рис. 1).

 

Рис. 1. Зависимость давленияидеального газа от объема при

постоянной температуре

 

Полученная кривая – гипер­бола, полученная при пос­тоянной температуре, назы­вается изотермой, а процесс, протекающий при постоян­ной температуре, – изотер­мическим. Закон Бойля – Мариотта – приближенный и при очень больших дав­лениях и низких темпера­турах для теплотехнических расчетов неприемлем.

 

Закон Г е й – Л ю с с а к а определяет зависимость объ­ема идеального газа от температуры при постоян­ном давлении. (Закон Жозефа Луи Гей-Люссака (1778 – 1850), французского химика и физика, установившего впервые этот закон в 1802 году: объём данной массы идеального газа при постоянном давлении линейно возрастает с ростом температуры, то есть 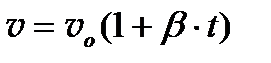, где - удельный объём при ; β – коэффициент объёмного расширения равный 1/273,16 на 1^оС.) Закон уста­новлен экспериментально в 1802 г. французским физи­ком и химиком Жозефом Луи Гей-Люссаком, именем которого назван. Исследуя на опыте тепловое расширение газов, Гей-Люссак от­крыл, что при неизменном давлении объемы всех газов увеличиваются при нагревании почти одинаково, т. е. при повышении температуры на 1°С объем некоторой массы газа увеличивается на 1/273 объема, который дан­ная масса газа занимала при 0°С.

Увеличение объема при нагревании на 1 °С на одну и ту же величину не случайно, а как бы является след­ствием закона Бойля – Мариотта. Вначале газ нагрева­ется при постоянном объеме на 1 °С, давление его увели­чивается на 1/273 начального. Затем газ расширяется при постоянной температуре, причем его давление уменьшается до начального, а объем во столько же раз увеличи­вается. Обозначив объем некоторой массы газа при 0°С через V ₀, а при температуре t °C через V_t запишем закон следующим выражением:

.    (8)

Закон Гей-Люссака также можно изобразить графи­чески.

 

Рис. 2. Зависимость объема идеального газа от температу­ры при постоянном

давлении

 

Используя уравнение (8) и принимая температуру равной 0°С, 273 °С, 546 °С, вычислим объем газа, равный соответственно V ₀, 2 V ₀, 3 V ₀. Отложим по оси абсцисс в некотором условном масштабе (рис. 2) температуры га­за, а по оси ординат – соответствующие этим темпера­турам объемы газа. Соединяя на графике полученные точки, получим прямую, представляющую собой график зависимости объема идеального газа от температуры при постоянном давлении. Такая прямая называется изобарой, а процесс, протекающий при постоянном дав­лении – изобарным.

Обратимся еще раз к графику изменения объема га­за от температуры. Продолжим прямую до пересечения, с осью абсцисс. Точка пересечения будет соответствовать абсолютному нулю.

Предположим, что в уравнении (8) значение V_t = 0, тогда имеем:

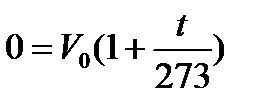
но так как V ₀ ≠ 0, следовательно, , откуда t = – 273°C. Но – 273°C=0К, что и требовалось дока­зать.

Представим уравнение Гей-Люссака в виде:

Помня, что 273+ t = Т, а 273 К=0°С, получим:

 или .       (9)

Подставляя в уравнение (9) значение удельного объема и принимая т =1 кг, получим:

 или                         (10)

Отношение (10) выражает закон Гей-Люссака, кото­рый можно сформулировать так: при постоянном давле­нии удельные объемы одинаковых масс одного и того же идельного газа прямо пропорциональны его абсолютным температурам. Как видно из уравнения (10), закон Гей-Люссака утверждает, что частное от деления удельногообъема данной массы газа на его абсолютную темпера­туру есть величина постоянная при данном постоянном давлении.

Уравнение, выражающее закон Гей-Люссака, в об­щем виде имеет вид

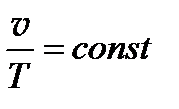(11)

и может быть получено из основного уравнения кине­тической теории газов. Уравнение (6) представим в виде

при p = const получаем уравнение (11). Закон Гей-Люссака широко применяется в технике. Так, на основе закона объемного расширения газов по­строен идеальный газовый термометр для измерения температур в пределах от 1 до 1400 К.

 

Закон Шарля устанавливает зависимость давле­ния данной массы газа от температуры при постоянном объеме.ЗаконЖана Шарля (1746 – 1823),французского ученого, установившего этот закон впервые в 1787 году, и уточненный Ж.Гей-Люссакомв 1802 году: давление идеального газа неизменной массы и объёма возрастает при нагревании линейно, то есть , где р _о – давление при t = 0°C.

Шарль определил, что при нагревании в по­стоянном объеме давление всех газов увеличивается почти одинаково, т.е. при повышении температуры на 1 °С давление любого газа увеличивается точно на1/273 того давления, которая данная масса газа имела при 0°С. Обозначим давление некоторой массы газа в сосуде при 0°С через р ₀, а при температуре t ° через p _t. При по­вышении температуры на 1°С давление увеличивается на 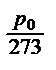, а при увеличении на t °Cдавление увеличива­ется на . Давление при температуре t °Cравно начальному плюс прирост давления или

;

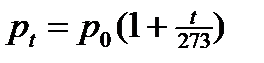.                            (12)

Формула (12) позволяет вычислить давление при лю­бой температуре, если известно давление при 0°С. В инженерных расчетах очень часто используют уравнение (закон Шарля), которое легко получается из соотношения (12).

Поскольку , а 273 + t = Т или 273 К = 0°С = Т ₀

Имеем

 или . (13)

При постоянном удельном объеме абсолютные давле­ния идеального газа прямо пропорциональны абсолют­ным температурам. Поменяв местами средние члены пропорции, получим

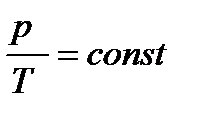 или .(14)

Уравнение (14) есть выражение закона Шарля в об­щем виде. Это уравнение легко вывести из формулы (6)

.

При V = const получаем общее уравнение закона Шарля (14).

Для построения графика зависимости данной массы газа от температуры при постоянном объеме воспользу­емся уравнением (13). Пусть, например, при температу­ре 273 К=0°С давление некоторой массы газа 98 кПа. По уравнению давление при температуре 373, 473, 573 °С соответственно будет 137 кПа (1,4 кгс/см²), 172 кПа (1,76 кгс/см²), 207 кПа (2,12 кгс/см²). По этим данным строим график (рис. 3). Полученная прямая называется изохорой, а процесс, протекающий при постоянном объеме, – изохорным.

 

Рис. 3. Зависимость давления газа от темпера­туры при постоянном объеме

 

v ₀

Поделиться:

Воспользуйтесь поиском по сайту: