 |
Ряды с положительными членами.
|
|
|
|
Ряды
Оглавление.
1. Основные понятия.
2. Необходимый признак сходимости.
3. Ряды с положительными членами.
4. Знакопеременные ряды.
5. Функциональные ряды.
6. Степенные ряды.
7. Ряд Тейлора.
8. Тригонометрический ряд (ряд Фурье).
Основные понятия
Рядом называется выражение вида

где  последовательность чисел или функций. Слагаемые
последовательность чисел или функций. Слагаемые  называются членами ряда. Если все члены ряда являются числами, то ряд называется числовым, если члены ряда - функции, то ряд называется функциональным.
называются членами ряда. Если все члены ряда являются числами, то ряд называется числовым, если члены ряда - функции, то ряд называется функциональным.
Рассмотрим числовой ряд

Этот ряд задан, если известен его общий член  , т.е. известно правило, по которому каждому номеру
, т.е. известно правило, по которому каждому номеру  ставится в соответствие вполне определенный член ряда.
ставится в соответствие вполне определенный член ряда.
Сумма конечного числа  первых членов ряда называется его
первых членов ряда называется его 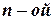 частичной суммой:
частичной суммой:

Конечный или бесконечный предел частичной суммы при  называется суммой ряда:
называется суммой ряда:

Ряд, имеющий конечную сумму, называется сходящимся. Если предел частичной суммы не существует или равен бесконечности, то ряд называется расходящимся.
Ряд, члены которого неотрицательны, называется положительным. Положительный ряд всегда имеет сумму; эта сумма будет конечной (и, следовательно, ряд – сходящийся), если его частичная сумма ограничена сверху, и бесконечной (а ряд – расходящийся), если суммы сверху неограниченны.
Если в ряде отбросить первые  членов, то получится ряд
членов, то получится ряд

называемым остатком ряда после  члена.
члена.
Необходимый признак сходимости
Теорема 1. Если ряд сходится, то сходится и любой из его остатков; обратно, из сходимости остатка вытекает сходимость исходного ряда.
Теорема 2. Если ряд сходится, то сумма  его остатка после
его остатка после  члена с возрастанием
члена с возрастанием  стремится к нулю:
стремится к нулю:  .
.
|
|
|
Теорема 3 (необходимый признак сходимости). Если ряд сходится, то его общий член стремится к нулю, т.е.
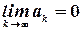
Отметим, что эти условия не является достаточными.
Следствие. Если общий член ряда к нулю не стремится, то ряд расходится.
Примеры рядов.
Геометрический ряд:

Геометрический ряд сходится тогда и только тогда, когда 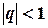 ; его сумма определяется формулой
; его сумма определяется формулой  .
.
Гармонический ряд

Гармонический ряд, как мы покажем позже, расходится.
Ряды с положительными членами.
Рассмотрим числовые ряды с положительными членами
 (А)
(А)
 (Б)
(Б)
Теорема4 (первый признак сравнения). Если для всех 
 ряд (Б) сходится, то сходится и ряд (А).
ряд (Б) сходится, то сходится и ряд (А).
Если для всех 
 ряд (Б) расходится, то расходится и ряд (А).
ряд (Б) расходится, то расходится и ряд (А).
Теорема 5 (второй признак сравнения). Если существует конечный и отличный от нуля предел  , то ряды (А) и (Б) сходятся и расходятся одновременно.
, то ряды (А) и (Б) сходятся и расходятся одновременно.
Теорема 6 (интегральный признак Коши). Если  - неотрицательная, невозрастающая функция при
- неотрицательная, невозрастающая функция при  , то ряд
, то ряд

сходится или расходится одновременно с интегралом

Пример. Исследовать, при каких 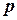 сходится ряд Дирихле
сходится ряд Дирихле

Если  то общий член ряда не стремится к нулю, поэтому ряд расходится. В случае
то общий член ряда не стремится к нулю, поэтому ряд расходится. В случае  применим интегральный признак Коши. Функция
применим интегральный признак Коши. Функция  положительна и не возрастает при
положительна и не возрастает при  . Пусть
. Пусть  . Положив
. Положив  . получим:
. получим:
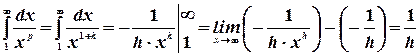
Поскольку интеграл сходится, то сходится и ряд Дирихле.
Если  , то
, то

Интеграл расходится, поэтому расходится и ряд Дирихле.
При  получается гармонический ряд. Тем самым мы доказали указанную ранее расходимость гармонического ряда.
получается гармонический ряд. Тем самым мы доказали указанную ранее расходимость гармонического ряда.
Итак, ряд Дирихле сходится при  , и расходится при
, и расходится при  .
.
Замечание. Сходимость многих рядов может быть исследована сравнением с соответствующим рядом Дирихле.
Пример. Исследовать сходимость ряда  .
.
Воспользуемся интегральным признаком Коши, для чего составим функцию  . Функция убывает, если ее производная меньше нуля (отрицательна). Найдем производную согласно формуле
. Функция убывает, если ее производная меньше нуля (отрицательна). Найдем производную согласно формуле 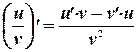 :
:

Эта производная отрицательна, т. к.  , следовательно, члены исследуемого ряда убывают с ростом
, следовательно, члены исследуемого ряда убывают с ростом  .
.
|
|
|
Теперь непосредственно используем признак Коши.

Теорема 7 (признак Д’Аламбера). Пусть для ряда (А) существует

Если  , то ряд (А) сходится, если
, то ряд (А) сходится, если  то ряд расходится. Если
то ряд расходится. Если 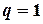 , то вопрос о сходимости ряда остается открытым.
, то вопрос о сходимости ряда остается открытым.
Теорема 8 (" радикальный" признак Коши). Пусть для ряда (А) существует

Если  , то ряд (А) сходится, если
, то ряд (А) сходится, если  то ряд расходится.
то ряд расходится.
Знакопеременные ряды
Ряд, содержащий как положительные, так и отрицательные члены, называется знакопеременным.
Знакопеременный ряд
 (В)
(В)
сходится, если сходится ряд, составленный из модулей его членов, т.е. ряд
 (Г)
(Г)
Примечание – обратное неверно. Например:

Ряд (В) в этом случае называется абсолютно сходящимся. Сумма абсолютно сходящегося ряда не зависит от порядка слагаемых.
Ряд, у которого любые два соседних члена имеют разные знаки, называется знакочередующимся.
Теорема 9 (признак Лейбница). Знакочередующийся ряд

сходится, если выполнены условия

Доказательство:
Частичная сумма с четным номером

Возрастает, т.к. состоит из положительных слагаемых. Ее можно представить в виде

Также можно записать
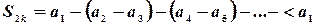
т.к.  . Следовательно,
. Следовательно,  .
.
Нечетная сумма  . Очевидно, что
. Очевидно, что

Теорема доказана.
Рассмотрим знакочередующийся ряд:
 .
.
Члены этого ряда монотонно убывают  , общий член ряда стремится к нулю
, общий член ряда стремится к нулю  . Следовательно, этот ряд сходится по признаку Лейбница.
. Следовательно, этот ряд сходится по признаку Лейбница.
Представим знакочередующийся ряд в виде:

где  - частичная сумма,
- частичная сумма,  - остаток ряда.
- остаток ряда.
Остаток ряда представим в виде:
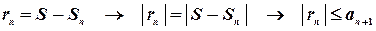
Вывод: погрешность при вычислении суммы знакочередующегося ряда не превосходит первого отброшенного члена.
Таким образом, сравнивая два ряда
 ,
,
можно сделать следующие выводы.
1. Если ряды (1) и (2) сходятся, то ряд (1) – абсолютно сходящийся.
2. Если ряд (2) расходится, а ряд (1) сходится, то ряд (1) называется условно сходящимся.
3. Если и ряды (1) и (2) расходятся, то ряд (1) – расходящийся ряд.
Свойство №1:
Если ряд сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его членов и сумма при этом не меняется.
Свойство №2:
Если ряд сходится условно, то при перестановке его членов сумма его может стать равной любому числу, а также можно сделать его расходящимся.
|
|
|
Пример.
Ряд  расходится или нет? Является ли он абсолютно сходящимся или нет?
расходится или нет? Является ли он абсолютно сходящимся или нет?
Рассмотрим ряд, составленный из модулей его членов
 .
.
Согласно признаку Д’Аламбера, найдем предел
 .
.
Отсюда следует, что ряд из модулей расходится, значит, нет и абсолютной сходимости.
Пример. Исследовать ряд  .
.
Рассмотрим ряд, составленный из модулей членов исследуемого ряда

и сравним его с гармоническим, расходящимся рядом  , для чего используем признак Д’Аламбера
, для чего используем признак Д’Аламбера

Отсюда вытекает, что абсолютной сходимости исходного ряда нет.
Для выяснения вопроса сходится ли ряд условно, рассмотрим необходимое условие сходимости, т.е. проверим условие 

Преобразуем его:
 ,
,
Откуда

Или

что эквивалентно  , что выполняется. Следовательно, элементы последовательности убывают. Проверим теперь второе условие – стремится ли к нулю
, что выполняется. Следовательно, элементы последовательности убывают. Проверим теперь второе условие – стремится ли к нулю  член последовательности
член последовательности
-  .
.
Итак, исходный ряд сходится условно.
Функциональные ряды.
Пусть дан функциональный ряд

т.е. ряд, члены которого  некоторые функции от
некоторые функции от  . При каждом фиксированном значении
. При каждом фиксированном значении  функциональный ряд становится числовым рядом
функциональный ряд становится числовым рядом

Если этот ряд сходится, то значение аргумента  называется точкой сходимости ряда. Множество всех точек сходимости
называется точкой сходимости ряда. Множество всех точек сходимости  функционального ряда называется его областью сходимости, а функция
функционального ряда называется его областью сходимости, а функция

- суммой данного ряда. Функция

называется остатком ряда.
Функциональный ряд  называется равномерно сходящимся в некотором промежутке, если, каково бы не было
называется равномерно сходящимся в некотором промежутке, если, каково бы не было  , существует такое
, существует такое  , не зависящее от
, не зависящее от  , что при
, что при  для всех
для всех  из данного промежутка выполняется неравенство
из данного промежутка выполняется неравенство

где  остаток ряда.
остаток ряда.
Теорема 9 (признак Вейерштрасса). Функциональный ряд  сходится абсолютно и равномерно в некотором промежутке, если существует сходящийся числовой ряд с положительными членами
сходится абсолютно и равномерно в некотором промежутке, если существует сходящийся числовой ряд с положительными членами

такой, что 
для всех  из данного промежутка.
из данного промежутка.
Ряд  называется мажорантным рядом для ряда
называется мажорантным рядом для ряда  .
.
Пример. Ряд
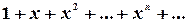
геометрическая прогрессия, ее сумма  . При
. При  ряд сходится, при
ряд сходится, при  - ряд расходится. Область сходимости
- ряд расходится. Область сходимости  .
.
Пример. Исследовать ряд
 .
.
Рассмотрим ряд, составленный из модулей его членов  . Так как
. Так как  , рассмотрим мажорантный ряд в виде:
, рассмотрим мажорантный ряд в виде:  . Для
. Для  члена имеем
члена имеем  . Мажоранта сходится, следовательно, исходный ряд сходится абсолютно.
. Мажоранта сходится, следовательно, исходный ряд сходится абсолютно.
|
|
|
Теорема 10. Если члены ряда (1)  непрерывны при
непрерывны при  и ряд этот сходится равномерно в замкнутом промежутке
и ряд этот сходится равномерно в замкнутом промежутке  , то его можно интегрировать почленно в данном промежутке
, то его можно интегрировать почленно в данном промежутке

(Интеграл от суммы равен сумме интегралов).
Пусть ряд (1) мажорируем на  , тогда его можно почленно интегрировать на любом
, тогда его можно почленно интегрировать на любом 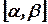 вложенном в
вложенном в  .
.
Доказательство. Пусть числовой ряд (2) 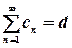 - мажорант,
- мажорант, 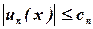
 . Ряды представим в виде
. Ряды представим в виде


Рассмотрим ряд  . Его частичную сумму
. Его частичную сумму  можно представить как
можно представить как

Требуется доказать, что

Имеем

Далее

Таким образом

Теорема 11. Если члены сходящегося ряда непрерывны при  и ряд
и ряд  сходится равномерно в замкнутом промежутке
сходится равномерно в замкнутом промежутке  , то ряд
, то ряд  можно дифференцировать почленно
можно дифференцировать почленно
 .
.
Доказательство: По условию теоремы ряд  сходится. Обозначим пока его сумму как
сходится. Обозначим пока его сумму как  , т.е.
, т.е.  . Согласно предыдущей теореме, этот ряд можно почленно интегрировать.
. Согласно предыдущей теореме, этот ряд можно почленно интегрировать.


 Что и т.д.
Что и т.д.
6. Степенные ряды.
Степенным называется функциональный ряд вида

где  - постоянные числа, называемые коэффициентами ряда. При
- постоянные числа, называемые коэффициентами ряда. При  ряд принимает вид
ряд принимает вид

Теорема 12 (признак Абеля). Если степенной ряд  сходится при
сходится при  , то он сходится абсолютно и равномерно при любом
, то он сходится абсолютно и равномерно при любом  , для которого
, для которого  .
.
Доказательство: Если ряд  сходится, то
сходится, то  , т.е.
, т.е.  . Возьмем
. Возьмем  , обозначим
, обозначим  . Рассмотрим теперь ряд
. Рассмотрим теперь ряд  , представив его в виде:
, представив его в виде:

Ряд  сходится, т.к. это геометрическая прогрессия с
сходится, т.к. это геометрическая прогрессия с  , следовательно, ряд
, следовательно, ряд  сходится абсолютно.
сходится абсолютно.
Теорема доказана.
Замечание. Степенной ряд можно сколько угодно раз почленно дифференцировать и интегрировать. Интервал сходимости от этого не изменится.
Радиусом сходимости степенного ряда  называется число
называется число 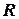 такое, что при
такое, что при 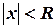 ряд сходится, а при
ряд сходится, а при  расходится. Интервал
расходится. Интервал  в этом случае называется интервалом сходимости указанного ряда. На концах промежутка
в этом случае называется интервалом сходимости указанного ряда. На концах промежутка  ряд может сходиться или расходиться.
ряд может сходиться или расходиться.
Степенной ряд сходится абсолютно и равномерно на любом отрезке, принадлежащем интервалу сходимости.
Радиус сходимости степенного ряда находится с помощью признака Д’Аламбера или признака Коши. Радиус сходимости можно вычислить по одной из формул

если соответствующий предел существует.
Действительно, исследуем абсолютную сходимость степенного ряда  , для чего рассмотрим предел.
, для чего рассмотрим предел.

Если  то ряд сходится абсолютно, если же
то ряд сходится абсолютно, если же  то ряд расходится. Величину
то ряд расходится. Величину  и называют радиусом сходимости ряда.
и называют радиусом сходимости ряда.
Пример. Исследовать ряд:

Радиус сходимости ряда  . Интервал сходимости
. Интервал сходимости  или
или  , откуда
, откуда  , следовательно
, следовательно  - интервал сходимости.
- интервал сходимости.
7. Ряд Тейлора.
Если функция  разлагается в степенной ряд
разлагается в степенной ряд
|
|
|

в некоторой окрестности точки  , т.е. в интервале
, т.е. в интервале  , то коэффициенты этого ряда определяются по формулам
, то коэффициенты этого ряда определяются по формулам

Следовательно, разложение функции в ряд будет иметь вид:

Ряд, стоящий в правой части формулы называется рядом Тейлора для функции  .
.
Это равенство выполняется, (ряд Тейлора сходится к  в интервале
в интервале  ), если остаток ряда Тейлора
), если остаток ряда Тейлора

стремится к нулю при неограниченном возрастании  , т.е.
, т.е.  при всех
при всех  из интервала
из интервала  .
.
Если  , то ряд Тейлора переходит в ряд Маклорена:
, то ряд Тейлора переходит в ряд Маклорена:

Разложение основных функций в ряд Тейлора.
1. 
2. 
3. 
4. 
5. 
6. 
7. 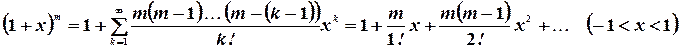
Примечание. Радиус сходимости ряда (7) будет равен:

При  ряд будет иметь вид:
ряд будет иметь вид:  .
.
При  дробь
дробь  будет иметь разложение
будет иметь разложение
 .
.
Тригонометрический ряд
Рядом Фурье функции  называется тригонометрический ряд
называется тригонометрический ряд
 (1)
(1)
Найдем выражения для коэффициентов ряда Фурье.
Для этого введем определения.
Функция  называется четной, если справедливо соотношение
называется четной, если справедливо соотношение

Функция  называется нечетной, если справедливо соотношение
называется нечетной, если справедливо соотношение

Функция  называется периодической, если справедливо соотношение
называется периодической, если справедливо соотношение

1. Найдем теперь выражение для коэффициента 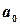 ряда Фурье.
ряда Фурье.
Для этого возьмем определенный интеграл от левой и правой частей тригонометрического ряда (1) в пределах от  до
до  :
:

Согласно введенным определениям  , т.к. синус функция нечетная. Действительно
, т.к. синус функция нечетная. Действительно

Аналогично,  . Действительно, хотя функция косинус является четной, но период этой функции равен
. Действительно, хотя функция косинус является четной, но период этой функции равен 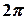 , поэтому
, поэтому
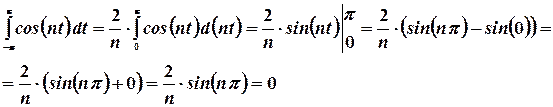
Далее, осталось последнее слагаемое:  .
.
Отсюда получаем  . И окончательно получим:
. И окончательно получим:

2. Найдем теперь выражение для коэффициентов  ряда Фурье.
ряда Фурье.
Для этого, умножим левую и правую части тригонометрического ряда (1) на 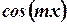 . В результате получим:
. В результате получим:

Проинтегрируем получившийся ряд в пределах от  до
до  .
.
При этом, как мы только что показали, учтем то обстоятельство, что в первом слагаемом будет интеграл вида:  . Следовательно, первое слагаемое в правой части будет равно нулю.
. Следовательно, первое слагаемое в правой части будет равно нулю.
Затем учтем, что в третьем слагаемом будет интеграл вида:  , т.к. согласно известной формуле тригонометрии
, т.к. согласно известной формуле тригонометрии
 .
.
Следовательно, под интегралом у нас будут нечетные функции, интеграл от которых в симметричных пределах равен нулю. Таким образом, и третье слагаемое в правой части будет равно нулю.
Следующее, второе слагаемое будет иметь вид:

т.к. под интегралом произведение двух четных функций.

т.к. 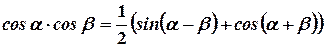 и интеграл от суммы равен сумме интегралов.
и интеграл от суммы равен сумме интегралов.
В результате получим, что исходный интеграл равен:

Поэтому справа все слагаемые будут равны нулю, за исключением слагаемого, для которого 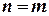 и оно будет равно с
и оно будет равно с  .
.
Отсюда, для коэффициентов  ряда (1) получим выражение:
ряда (1) получим выражение:

3. Для нахождения коэффициента  , умножив левую и правую части тригонометрического ряда на
, умножив левую и правую части тригонометрического ряда на  . В результате получим:
. В результате получим:

Опять же проинтегрируем получившийся ряд в пределах от  до
до  . При этом учтем то обстоятельство, что
. При этом учтем то обстоятельство, что 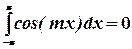 и, следовательно, первое слагаемое равно нулю. Второе слагаемое также равно нулю, т.к.
и, следовательно, первое слагаемое равно нулю. Второе слагаемое также равно нулю, т.к.  .
.
Осталось третье слагаемое. Для его нахождения необходимо найти интеграл:  . Его представим в виде:
. Его представим в виде:

т.к. произведение двух нечетных функций под знаком интеграла дает четную функцию.

т.к.  ,
,
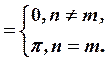
Отсюда 

4. Окончательно запишем:

Теорема 13. Пусть –  ограниченная, кусочно-непрерывная
ограниченная, кусочно-непрерывная 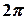 – периодическая функция, следовательно,
– периодическая функция, следовательно,  можно представить рядом Фурье:
можно представить рядом Фурье:

Если функция  с периодом
с периодом 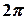 кусочно-дифференцируема в промежутке
кусочно-дифференцируема в промежутке  , то ее ряд Фурье сходится в любой точке
, то ее ряд Фурье сходится в любой точке  и имеет сумму:
и имеет сумму:

В частности, в точке непрерывности функции  сумма ее ряда Фурье равна значению самой функции
сумма ее ряда Фурье равна значению самой функции  , т.к.
, т.к. 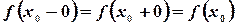 . На концах промежутка
. На концах промежутка  имеем
имеем 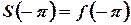 ,
,  , если функция
, если функция  непрерывна в точках
непрерывна в точках  и
и  , если она разрывна в этих точках.
, если она разрывна в этих точках.
Кроме того.
Если функция  – четная, то ее разложение в ряд Фурье имеет вид
– четная, то ее разложение в ряд Фурье имеет вид

Если функция  – нечетная, то ее разложение имеет вид
– нечетная, то ее разложение имеет вид

Далее рассмотрим теперь функцию произвольного периода.
Пусть функция  - периодическая, с периодом
- периодическая, с периодом  . В этом случае, для сведения ее к "классическому" ряду Фурье, введем переменную
. В этом случае, для сведения ее к "классическому" ряду Фурье, введем переменную 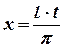 , где
, где  , а также функцию
, а также функцию  . Эта функция периодическая, с периодом
. Эта функция периодическая, с периодом 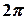 . Действительно
. Действительно

Поэтому ее разложение в ряд Фурье будет иметь вид:

Обозначив  , получим
, получим

Коэффициенты этого ряда будут находиться по аналогичным формулам

Частные случаи.
Функция  - четная
- четная
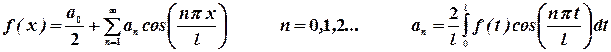
Функция  - нечетная
- нечетная

Пример.
Разложить в ряд Фурье функцию  на интервале
на интервале 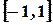 .
.
Функция  нечетная, поэтому
нечетная, поэтому 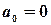 и
и  .
.

Следовательно, разложение в ряд Фурье будет иметь вид

Интеграл Фурье.
f(x) – ограничена, кусочно-непрерывна, абсолютно интегрируется на (-∞, +∞), т.е.  сходится
сходится






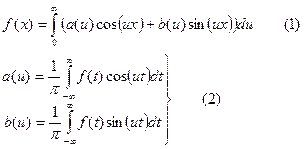
Это от предыдущего примера:




|
|
|


