 |
Примеры выполнения задания
|
|
|
|
Д-7 Применение принципа возможных перемещний для определения реакций связей составной конструкции.
Некоторые положения теории
Определение реакций связей с использованием принципа возможных перемещений рекомендуется осуществлять по следующей методике.
1 Отбросить ту связь, реакции которой требуется определить. Действие связи заменить ее реакцией, которую добавляют к активным силам.
2 Системе сообщить возможное перемещение.
3 Определить элементарные работы всех активных сил на возможных перемещениях.
4 Установить зависимость между возможными перемещениями и выразить их через возможное перемещение одной точки или один возможный угол поворота.
5 В соответствии с принципом возможных перемещений, приравнять сумму активных сил на возможных перемещениях нулю. Сократить возможное перемещение, через которое выражены перемещения вcех точек, и определить искомую реакцию.
Условие задания Д-7
На основании исходных данных (таблица 7.1) и используя принцип возможных перемещений, определить реакции связей составной конструкции, изображенной на рисунке 7.1.
Таблица 7.1 – Исходные данные к заданию Д-7
| Вариант | l, м | a, град | F, кН | M, кН×м | q, кН/м | Вариант | l, м | a, град | F, кН | M, кН×м | q, кН/м |
| 0,5 | |||||||||||
| 0,6 | 0,6 | ||||||||||
| 1,5 | |||||||||||
| 0,5 | |||||||||||
| 0,8 | |||||||||||
| 0,5 | |||||||||||
| 0,7 | |||||||||||
| 0,5 | |||||||||||
| — | |||||||||||
| 0,5 |
| 
| ||||||
| 
| ||||||
| 
| ||||||
| 
|
Рисунок 7.1 (начало)
| 
| ||||
| 
| ||||
| 
| ||||
| 
|
Рисунок 7.1 (продолжение)
| 
| ||||
| 
| ||||
| 
| ||||
| 
|
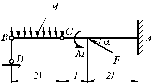
Рисунок 7.1 (продолжение)
| 
| ||||
| 
| ||||
 | 
|
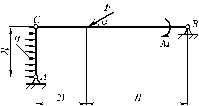
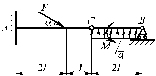
Рисунок 7.1 (окончание)
Примеры выполнения задания
Определить реакции связей составной конструкции, изображенной на рисунке 7.2. Дано: l = 1 м; a =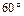 
; F = 6 кН; M = 11 кН×м; q = 2 кН/м.
Решение
1 Изображаем исследуемую систему и указываем действующие на нее силы (рисунок 7.3). Равномерно распределенную нагрузку заменяем сосредоточенной силой 
, приложенной в центре отрезка CE. Следовательно, 
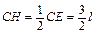. Модуль силы определяется следующим образом: 
.
В точке A действует реакция связи типа гладкая поверхность 
, направленная перпендикулярно опорной поверхности. В точке B на тело действует связь типа жесткая заделка. Реакция данной связи состоит из силы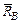 
и момента заделки MB. Силу 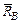разложим на две составляющие 
. Таким образом, необходимо определить 4 величины: RA, RBx, RBy, MB.
2 Приступаем к определению искомых реакций.
2.1 Определим реакцию RA.
а) отбросим связь, соответствующую силе RA. Тогда сила RA перейдет в разряд активных, а точка A получит возможность перемещаться. Делаем рисунок и указываем активные силы (рисунок 7.4);
б) сообщаем системе возможные перемещения. Так как в точке B действует жесткая заделка, то тело BC останется неподвижным. Следовательно, возможным перемещением тела AC может быть только поворот вокруг точки С на бесконечно малый угол dj. Укажем возможные перемещения точек приложения сил (точек A и D). Так как точка C – центр вращения тела AC, то вектор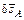 
направлен перпендикулярно отрезку AC, а вектор возможного перемещения 
направлен перпендикулярно отрезку DC;
|
|
|
в) определим элементарные работы сил на указанных перемещениях:
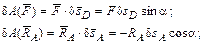
г) установим связь между возможными перемещениями d sA и d sD. Перемещение d sA связано с углом поворота тела AC следующим образом: 
. Следовательно, 
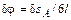. Для перемещения d sD можно записать: 
. Подставим ранее полученное выражение для угла dj:
;
д) запишем формулировку принципа возможных перемещений:
.
Подставим выражение для элементарных работ:
.
Воспользуемся выведенной формулой для перемещения d sD:
.
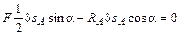Разделим полученное равенство на d sA и выразим искомую силу RA:
.
Подставим известные численные значения:
.
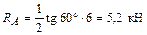2.2 Определим горизонтальную составляющую реакции жесткой заделки RBx:
а) отбросим связь, препятствующую горизонтальному смещению точки B, заменив жесткую заделку скользящей (направляющими). Тогда сила RBx перейдет в разряд активных. Делаем рисунок и указываем активные силы (рисунок 7.5);
б) сообщаем системе возможные перемещения. Точка B может перемещаться только горизонтально 
. Так как реакция в точке B запрещает поворот, то тело BC будет двигаться поступательно. Тогда 
и 
. Кроме того, 
и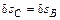 
. Таким образом, тело BC смещается на 
. Перемещение точки A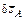 
направлено параллельно опорной поверхности (см. рисунок 7.5). Для того чтобы указать возможное перемещение тела AC найдем его мгновенный центр перемещений. МЦП тела совпадает с мгновенным центром скоростей. Векторы возможных скоростей точек совпадают по направлению с векторами возможных перемещений. Следовательно, мгновенный центр скоростей будет лежать на пересечении перпен-дикуляров, проведенных из точек A и C к векторам их возможных перемещений (точка P). МЦП тела является также мгновенным центром вращения. Следовательно, возможное перемещение тела AC представляет собой поворот вокруг точки P на угол dj. Смещение точки приложения силы 
направлено перпендикулярно отрезку DP (см. рисунок 7.5);
|
|
|
в) определим элементарные работы сил на указанных возможных перемещениях:
Так как тело BC движется поступательно, то момент M работы не совершает. Сила приложена к вращающемуся телу AC. Следовательно, работу этой силы на возможном угле поворота можно определить по работе момента:
.
Здесь 
– момент силы относительно точки P, вокруг которой происходит возможное вращение тела AC. Для определения этого момента силу удобно разложить на горизонтальную 
и вертикальную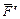 
составляющие. В соответствии с правилом определения проекции силы на ось, модули этих составляющих будут иметь следующие значения:
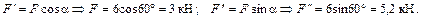Момент силы 
относительно точки P равен сумме моментов сил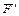 
и 
. Тогда 
.
Момент силы относительно точки P совпадает по направлению с углом поворота dj, а момент силы 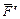– противоположен повороту. Следовательно, первое слагаемое в правой части последнего равенства будет положительным, а второе — отрицательным:
.
Определим длину отрезка PC. В прямоугольном треугольнике ACP угол C равен 
, а угол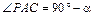 
. Следовательно,
.
Подставим выражения для модулей составляющих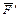 
и 
в формулу для работы силы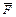 
:
;
г) установим связь между возможным перемещением d sB и углом dj. Для определения этой связи используем метод общей точки. Общей для звеньев AC и BC является точка C. Так как тело BC движется поступательно, то 
. С другой стороны, точка C принадлежит телу AC, для которого точка P является мгновенным центром скоростей. Следовательно,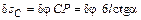 
. Тогда
;
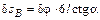д) запишем формулировку принципа возможных перемещений:
.
Подставим выражения для элементарных работ:
.
Воспользуемся ранее выведенной формулой для d sB:
.
Разделим полученное равенство на 
:
.
Выразим искомую силу RBx:
.
Подставим известные численные значения
.
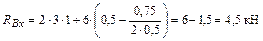2.3 Определим вертикальную составляющую реакции жесткой заделки RBy:
а) отбросим связь, препятствующую вертикальному смещению точки B, заменив жесткую заделку скользящей. Тогда сила 
перейдет в разряд активных. Делаем рисунок и указываем активные силы (рисунок 7.6);
|
|
|
б) сообщаем системе возможные перемещения. Точка B может двигаться только вертикально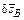 
. Так как реакция в точке B препятствует повороту тела BC, то BC движется поступательно. Тогда 
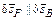и . Кроме того, 
и 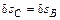. Таким образом, тело BC смещается на 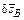. Перемещение точки A 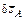направлено параллельно опорной поверхности (см. рисунок 7.6). Для того чтобы указать возможное перемещение тела AC найдем его мгновенный центр перемещений. Мгновенный центр перемещений будет лежать на пересечении перпендикуляров, проведенных из точек A и C к векторам их возможных перемещений. Видим, что МЦП тела AC совпадает с точкой A. Следовательно, возможное перемещение тела AC представляет собой поворот вокруг точки A на угол dj. Возможное перемещение точки D направлено перпендикулярно отрезку AD;
в) определим элементарные работы сил на указанных перемещениях:
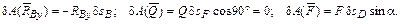
Так как тело BC движется поступательно, то момент M работы не совершает;
г) установим связь между возможными перемещениями d sD и d sB. Точка C – общая для тел AC и BC. Так как тело BC движется поступательно, то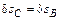 
. Тело AC вращается вокруг точки A. Следовательно,
.
Для перемещения точки D можно записать: 
. Подставим выражение для угла поворота:
;
д) запишем формулировку принципа возможных перемещений:
.
Подставим выражения для элементарных работ сил:
.
Воспользуемся выражением для d sD:
.
Следовательно: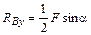 
. Подставим численные значения:
.
2.4 Определим момент заделки MB:
а) отбросим связь, препятствующую вращению тела BC, заменив жесткую заделку цилиндрическим шарниром. При этом момент MB перейдет в разряд активных силовых факторов. Делаем рисунок (рисунок 7.7), указываем активные силы и пары сил;
б) сообщаем системе возможные перемещения. Тело BC поворачивается вокруг точки B на возможный угол dj1. Для определения положения МЦП тела AC укажем возможные перемещения точек A и C. Перемещение точки A направлено параллельно опорной поверхности. Так как тело BC вращается вокруг точки B, то вектор возможного перемещения точки C направлен перпендикулярно отрезку BC. МЦП тела AC лежит на пересечении перпендикуляров, проведенных к векторам возможных перемещений точек A и C (см. рисунок 7.7). Таким образом, возможное перемещение тела AC – поворот вокруг точки P на угол dj2. Возможное перемещение точки приложения силы () направлено перпендикулярно отрезку DP. Возможное перемещение точки приложения силы (
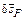) направлено перпендикулярно отрезку BF;
в) определим элементарные работы сил на указанных перемещениях. Пары сил с моментами M и MB приложены к телу BC, которое поворачивается на угол dj1. Работа этих пар определяется следующим образом:
.
Здесь учтено, что моменты M и MB направлены противоположно повороту. Работу силы 
определим как работу момента этой силы относительно точки B:
|
|
|
.
Известно, что 
. Следовательно,
.
Положение мгновенного центра скоростей тела AC на рисунке 7.7 совпадает с положением МЦП, определенным при нахождении реакции RBx (см. рисунок 7.5). Следовательно, для определения работы силы 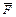можно воспользоваться формулой, выведенной при нахождении RBx:
;
г) установим связь между углами поворота dj1 и dj2. Воспользуемся методом общей точки. Общей для тел AC и BC является точка C. Тело BC вращается вокруг точки B. Следовательно, 
. С другой стороны, для скорости точки C можно записать: 
. Приравняем правые части выражений для скорости vC:
;
д) запишем формулировку принципа возможных перемещений:
.
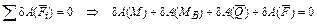Подставим выражения для элементарных работ:
.
Воспользуемся выведенной формулой для угла dj1:
.
Разделим последнее равенство на dj2 и выразим момент MB:
.
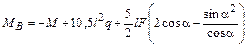Подставим известные численные значения:
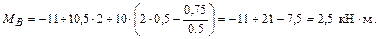
3 Проверим правильность решения задачи.
Изобразим исследуемую систему и укажем все действующие на нее силы (рисунок 7.8). На систему тел действует произвольная плоская система сил. Следовательно, необходимо составить три уравнения равновесия:
1) сумма проекций сил на ось x должна быть равна нулю:
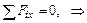
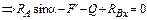; (7.1)
2) сумма проекций сил на ось y должна быть равна нулю:
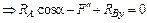. (7.2)
Здесь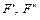 
– модули горизонтальной и вертикальной компонент силы соответственно;
3) сумма моментов всех сил относительно любой точки должна быть равна нулю. Уравнение моментов будем составлять относительно точки A
. (7.3)
Подставим в уравнения равновесия (7.1) – (7.3) известные численные значения и найденные ранее величины реакций связей:
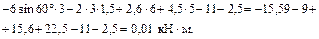
Так как при округлении до десятых долей правые части равенств обращаются в ноль, то найденные значения реакций связей удовлетворяют условиям равновесия системы тел.
Ответ: RA = 5,2 кН; RBx = 4,5 кН; RBy = 2,6 кН; MB = 2,5 кН×м.
|
|
|
