 |
Расчет энтропии и построение гистограммы частот
|
|
|
|
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Им. Н.Э. БАУМАНА
Факультет: Информатика и системы управления
Кафедра: Информационная безопасность (ИУ8)
ОБЛАЧНЫЕ ВЫЧИСЛЕНИЯ
Домашнее задание
«Анализ характеристик временного ряда»
Преподаватель:
Басараб М. А.
Студент:
Эрендженова Д. С.
Группа:
ИУ8-102
Москва 2017
СОДЕРЖАНИЕ
СОДЕРЖАНИЕ. 2
ОСНОВНАЯ ЧАСТЬ. 3
1 Цель работы.. 3
2 Практическая часть. 3
2.1 Выбор временного ряда. 3
2.2 Расчет статистических величин. 4
2.3 Построение нормированного временного ряда. 5
2.4 Расчет энтропии и построение гистограммы частот. 6
2.5 Построение фазовых диаграмм. 8
2.6 R/S-анализ и расчет показателя Херста и фрактальной размерности 8
2.7 Спектральная плотность мощности и вариация Аллана. 9
ЗАКЛЮЧЕНИЕ. 11
СПИСОК ЛИТЕРАТУРЫ.. 12
ОСНОВНАЯ ЧАСТЬ
Цель работы
1. Выбрать временной ряд, содержащий не менее 1000 отсчетов.
2. Рассчитать среднее, дисперсию, СКО, размах (вариацию).
3. Построить нормированный временной ряд с нулевым средним.
4. Для полученного нормированного ряда:
· рассчитать энтропию и построить гистограмму частот;
· построить фазовые диаграммы (2D, 3D);
· выполнить R/S-анализ;
· рассчитать показатель Херста и фрактальную размерность;
· построить график спектральной плотности мощности и вариации Аллана.
Практическая часть
Выбор временного ряда
В качестве исследуемого временного ряда выбран временной ряд значений уровня сахара в крови человека (в ммоль/литр). Измерения уровня сахара проводились каждые 5 минут. Количество отсчетов – 1024.

Рисунок 1 – Временной ряд в табличном виде в Microsoft Excel
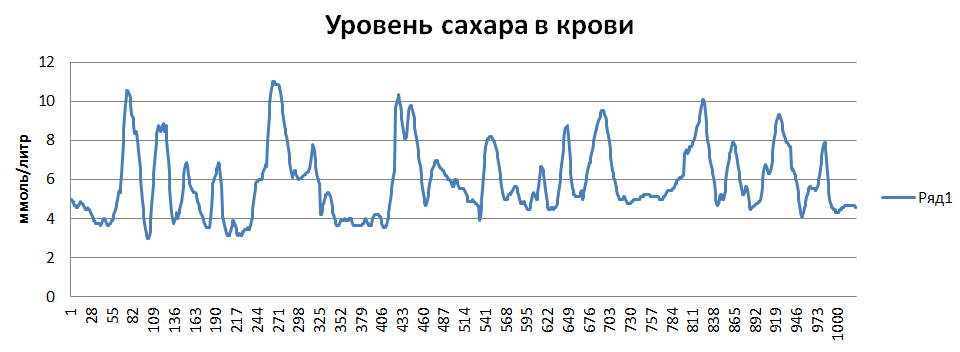
Рисунок 2 – Временной ряд в виде графика в Microsoft Excel
|
|
|
Расчет статистических величин
Среднее значение временного ряда находится следующим образом:

где N – количество отсчетов, xi – i -ое значение временного ряда.
Вычислим среднее по формуле (1), используя встроенные функции Microsoft Excel:
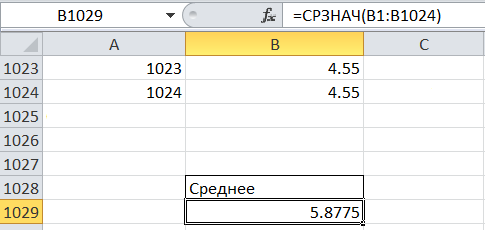
Рисунок 3 – Вычисление среднего значения в Microsoft Excel
Как видно из рисунка 3, среднее значение равно 5,8775.
Размах вариации (размах колебаний) представляет собой разность между максимальным (xmax) и минимальным (xmin) значениями временного ряда и определяется по формуле:

На рисунке 4 показаны максимальное и минимальное значения ряда, а также вычисленный по формуле (2) размах вариации:
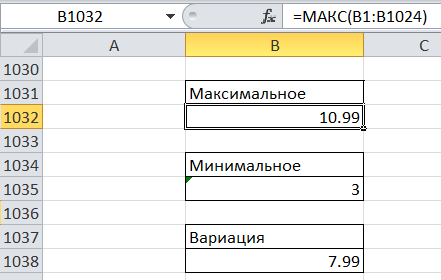
Рисунок 4 – Максимальное, минимальное значения и вариация
Дисперсию найдем по следующей формуле:

Среднее квадратическое отклонение (СКО) определяется как квадратный корень из дисперсии.
Вычисленные значения дисперсии и СКО представлены на рисунке 5:

Рисунок 5 – Дисперсия и СКО временного ряда
Построение нормированного временного ряда
Нормированный временной ряд с нулевым средним получим путем вычитания из исходного временного ряда среднего значения (рис. 6):
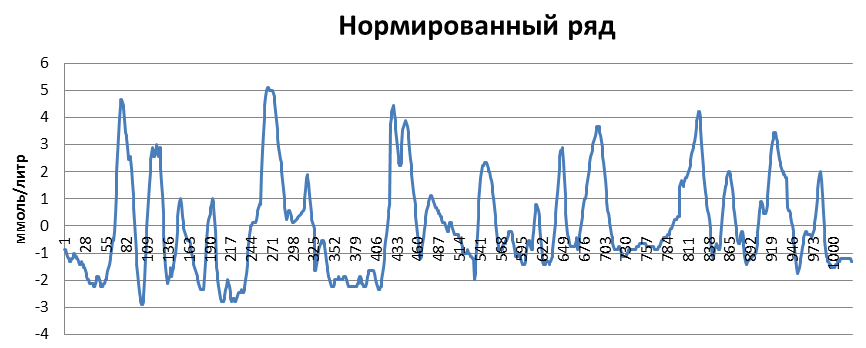
Рисунок 6 – Нормированный временной ряд
Расчет энтропии и построение гистограммы частот
При большом объеме выборки N выбирают такое число интервалов k, чтобы в интервалы попадало число наблюдений не менее 5-10. Выберем k = 10.
Тогда ширина интервала будет равна:

При этом максимальное и минимальное значение нормированного временного ряда будет соответственно равно 5,1125 и -2,8755.
Посчитаем количество точек, попавших в каждый интервал (рис. 7):

Рисунок 7 – Частота попадания значений в заданные интервалы
Заметим, что суммарное количество точек должно быть равно количеству отсчетов.
Построим гистограмму частот (рис. 8):

Рисунок 8 – Гистограмма частот
Энтропия по Шеннону рассчитывается по следующей формуле:
|
|
|

где pi – вероятность того, что значение ряда попало i -ый интервал.
Вероятность pi есть отношение количества точек, попавших в i -ый интервал, к общему количеству точек (всего 1024):

Рисунок 9 – Вычисление вероятности попадания значения в заданный интервал
Тогда по формуле (4) найдем энтропию:
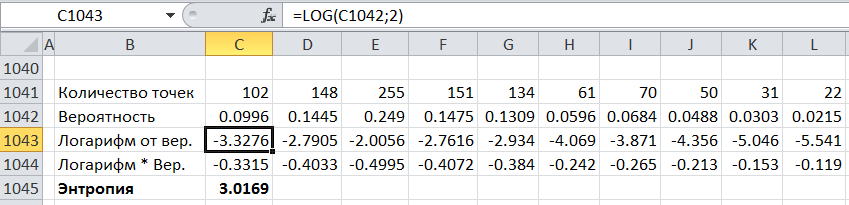
Рисунок 10 – Вычисление энтропии
Из рисунка 10 видно, что энтропия равна 3,0169.
|
|
|


