Определение опорных реакций

ИРКУТСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

 

Институт Архитектуры и строительства

 

Кафедра «Сопротивление материалов и строительная механика»

 

 

КУРСОВАЯ РАБОТА ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ

 

ЗАДАЧА 1

 

Расчет статически определимых балок на прочность

 

Выполнил студент группы ___________________________________

шифр И.О. Фамилия подпись

 

Руководитель _________________________

 

 

Иркутск 2016

 

1.1 Для консольной балки требуется:

 

1 Построить эпюры Q_y и M_x;

 

2 Подобрать по M_max размеры сечений: круглого, прямоугольного, состоящего из 2-х швеллеров.

Исходные данные: [σ] = 160 МПа, h/b = 2.

 

Дано: Консольная балка; L = 1 м; M = 30 кН*м; q= 40 кН/м; F = 50 кН (см. приложение А).

 

1 Построение эпюр Q_y и M_x

Так как в данной задаче балка закреплена при помощи жесткой заделки, в месте закрепления будут возникать 3 связи: H_B, R_B и M_B. Но так как их значения неизвестны изначально, то и не стоит их рассматривать (они определятся уже после построения эпюр Q_y и M_x). Поэтому можно сразу переходить непосредственно к рассмотрению каждого участка балки. Необходимо будет сделать разрезы в каждой из них. Затем, отбросив одну из частей, заменить ее действие соответствующим изгибающим моментом M_x и поперечной силой Q_y – разумеется, следуя общепринятому правилу знаков.

 

Итак, рассмотрим каждый из участков – всего их будет 3 (см. приложение А), и составим уравнения поперечных сил и изгибающих моментов на каждом из них:

 

I участок: 0 ≤ z₁ ≤ L

 

Q_y(z₁) = 0

 

M_x(z₁) = + M = 30 кНм = const

 

II участок: 0 ≤ z₂ ≤ L

 

Q_y(z₂) = - q*z₂ (линейное уравнение)

 

Тогда Q_y (z₂ = 0) = – 40*0 = 0

 

Q_y (z₂ = L = 1) = – 40*1= - 40 кН

M_x(z₂) = - q* + M (квадратное уравнение)

 

Тогда M_x(z₂ = 0) = - 40* + 30 = 30 кНм

 

M_x(z₂ = L = 1) = - 40* + 30 = 10 кНм

 

 

III участок: 0 ≤ z₃ ≤ L

 

Q_y(z₃) = - F – q*(z₃ + 1) (линейное уравнение)

 

Тогда Q_y (z₃ = 0) = - 50 – 40*(0 + 1)= - 90 кН

 

Q_y (z₃ = L = 1) = -50 – 40*(1 + 1)= - 130 кН

M_x(z₃) = - F*z₃ + M – q* (квадратное уравнение)

 

Тогда M_x(z₃ = 0) = - 50*0 + 30 – 40* = 10 кНм

 

M_x(z₃ = L = 1) = - 50*1 + 30 – 40* = - 100 кНм

 

По полученным значениям строятся соответственно эпюры Q_y и M_x (см. приложение А).

 

2 Подобрать по M_max размеры сечений: круглого, прямоугольного, состоящего из 2-х швеллеров

Для начала необходимо определить максимальное значение изгибающего момента M_max – по модулю. Из эпюры M_x видно, что это значение равно 100 кНм.

Рассчитываем требуемый момент сопротивления сечения из условия прочности по нормальным напряжениям:

 

= = = 0.625*10^-3 м³ = 625 см³

 

Теперь можно определить размеры сечений различной формы:

 

Круглое поперечное сечение

 

= => = = 18.534 см

A = = = 269.8 см²

 

Прямоугольное поперечное сечение

 

По условию соотношение сторон в таком сечении: =

 

= => = = 9.787 см

9.787 * 2 = 19.574 см

 

Следовательно, A = см²

Сечение, состоящее из двух швеллеров

 

=> = = 312.5 см³

 

По таблице сортамента выбираем наиболее подходящий швеллер – швеллер № 27: = 2*308 = 616 см³.

 

Площадь сечения швеллера: A = = 2*35.2 = 70.4 см²

 

Поскольку момент сопротивления сечения несколько меньше требуемого, необходимо определить перегрузку по напряжениям:

 

= = 162.34 МПа > [σ]

 

 

Так как величина перегрузки – не превышает 5%, то надежность конструкции можно считать достаточной.

 

 

1.2 Для балки на шарнирных опорах требуется:

 

1 Определить опорные реакции;

 

2 Построить эпюры Q_y, M_x;

 

3 Подобрать по M_max размеры двутаврового сечения;

 

4 Произвести полную проверку прочности (по нормальным, касательным и эквивалентным напряжениям) для двутаврового сечения.

Исходные данные: [σ] = 160 МПа, [τ] = 80 МПа.

 

Дано: Балка на шарнирных опорах; L = 1 м; M = 30 кН*м; q= 40 кН/м; F = 50 кН (см. приложение Б).

 

Определение опорных реакций

Так как в данной задаче балка закреплена при помощи двух опор – шарнирно-неподвижной и шарнирно-подвижной, то для начала необходимо будет определить величины и направления реакций, возникающих в этих опорах: H_B, R_B и R_C.

Для этого надо составить уравнения равновесия, определив из них значения опорных реакций. При этом из расчетной схемы балки видно, что реакция H_B = 0, так как на балку не действует ни одна продольная сила.

 

ΣM_B = 0: - q*2L*5L – M - F*5L + R_C*4L = 0

 

Отсюда R_C = (q*2L*5L + M + F*5L) /(4L) = (40*2*5 + 30 + 50*5*1) /(4*1) = + 170 кН

 

ΣM_C = 0: q*L*2L + M + F*L + R_B*4L = 0

 

Отсюда R_B = - (q*L*2L + M + F*L) /(4*L) = - (40*1*2 + 30 + 50*1) /(4*1) = - 40 кН

Положительные значения свидетельствуют о том, что первоначальное направление реакций выбрано верно. Отрицательные означают, что необходимо поменять первоначально выбранное направление данной реакции на противоположное.

Итак, проверим, правильно ли найдены непосредственно значения реакций R_B и R_C:

 

ΣF_Y = 0: - q*2L – F - R_B + R_C = 0

 

- 40*2 – 50 - 40 + 170 = 0

 

- 170 + 170 = 0

 

0 = 0

 

Отсюда вино, что, раз проверка сходится, то значения и направления реакций R_B и R_C найдены верно.

 

 

2 Построение эпюр Q_y, M_x

 

Теперь можно переходить к рассмотрению каждой из составных частей балки. Необходимо будет сделать разрезы в каждой из них. Затем, отбросив одну из частей, заменить ее действие соответствующим изгибающим моментом M_x и поперечной силой Q_y – разумеется, следуя общепринятому правилу знаков.

Итак, рассмотрим каждый из участков – всего их будет 3 (см. приложение Б), и составим уравнения поперечных сил и изгибающих моментов на каждом из них:

 

I участок: 0 ≤ z₁ ≤ 4L

 

Q_y(z₁) = - R_B = - 40 кН= const

 

M_x(z₁) = + M – R_B*z₁ (линейное уравнение)

 

Тогда M_x(z₁ = 0) = + 30 - 40*0 = 30 кНм

 

M_x(z₁ = 4L = 4) = + 30 - 40*4 = - 130 кНм

 

II участок: 0 ≤ z₂ ≤ L

 

Q_y(z₂) = R_C - R_B - q*z₂ (линейное уравнение)

 

Тогда Q_y (z₂ = 0) = 170 – 40 – 40*0 = 130 кН

 

Q_y (z₂ = L = 1) = 170 – 40 – 40*1 = 90 кН

M_x(z₂) = R_C*z₂ - - R_B*(z₂ + 4) + M (квадратное уравнение)

 

Тогда M_x(z₂ = 0) = 170*0 - - 40*(0 + 4) + 30 = - 130 кНм

 

M_x(z₂ = L = 1) = 170*1 - - 40*(1 + 4) + 30 = - 20 кНм

 

III участок: 0 ≤ z₃ ≤ L

 

Q_y(z₃) = R_C - R_B - F – q*(z₃ + 1) (линейное уравнение)

 

Тогда Q_y (z₃ = 0) = 170 - 40 - 50 – 40*(0 + 1) = 40 кН

 

Q_y (z₃ = L = 1) = 170 - 40 - 50 – 40*(1 + 1) = 0

M_x(z₃) = R_C*(z₃ + 1) - F*z₃ – q* – R_B*(z₃ + 5) +M (квадратное уравнение)

 

Тогда M_x(z₃ = 0) = 170*(0 + 1) - 50*0 – 40* – 40*(0 + 5) +30 = - 20 кНм

 

M_x(z₃ = L = 1) = 170*(1 + 1) - 50*1 – 40* – 40*(1 + 5) +30 = 0

 

По полученным значениям строятся соответственно эпюры Q_y и M_x (см. приложение Б).

 

3 Подобрать по M_max размеры двутаврового сечения

Для начала необходимо определить максимальное значение изгибающего момента M_max – по модулю. Из эпюры M_x видно, что это значение равно 130 кНм.

Рассчитываем требуемый момент сопротивления сечения из условия прочности по нормальным напряжениям:

 

= = = 0.8125*10^-3 м³ = 812.5 см³

 

Теперь переходим к определению размеров двутаврового сечения:

 

По таблице сортамента выбираем наиболее подходящий двутавр – двутавр № 36: 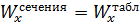= 743 см³ – ближайший

 

Площадь сечения двутавровой балки: A = = 61.9 см²

 

Поскольку момент сопротивления сечения несколько меньше требуемого, необходимо определить перегрузку по напряжениям:

 

= = 174.97 МПа > [σ]

 

 

Так как величина перегрузки – превышает 5%, то при заданных нагрузках такая конструкция не является надежной.

 

В таком случае из таблицы сортамента выбираем следующий номер двутаврового сечения – профиль двутаврового сечения № 40: 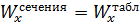= 947 см³

 

Площадь сечения двутавровой балки: A = = 71.4 см²

 

Поскольку момент сопротивления сечения несколько меньше требуемого, необходимо определить перегрузку по напряжениям:

 

= = 137.28 МПа < [σ]

 

 

Так как – превышает 5%, то при заданных нагрузках такая конструкция является излишне надежной.

 

Поделиться:

Воспользуйтесь поиском по сайту: