 |
Фундаментальные физические константы
|
|
|
|
Фотоэффект
Задача 7.1. Какой максимальный заряд Q max возможно сообщить платиновому шарику с радиусом R = 1 см, облучая его ультрафиолетом? Длина волны излучения λ = 200 нм.
| Дано: R = 1 см = 10–2м λ = 200 нм = 2·10–7м |
| Q max –? |
Решение:
При облучении металлического шарика светом возникает явление внешнего фотоэффекта – вырывание с поверхности шарика электронов, в результате чего шарик приобретает положительный заряд. Когда величина приобретенного заряда достигает определенного значения Q max, создаваемое им электростатическое поле препятствует удалению электронов от шарика, т.е. создает задерживающий потенциал. Электроны больше не могут покидать шарик, и его заряд больше не изменяется, и фотоэффект прекращается.
Уравнение Эйнштейна для фотоэффекта:
 ,
| (7.1) |
где 
– энергия фотона; 
– частота излучения; 
– длина волны излучения; 
м/с – скорость света; 
– работа выхода электронов из металла, по таблице находим ее значение для платины: 
; 
– максимальная кинетическая энергия электрона.
Если электрон не может покинуть шарик, значит, его кинетическая энергия не превышает потенциальную энергию его взаимодействия с заряженным шариком, т.е. 
. Потенциальная энергия электрона у поверхности шарика по модулю равна
,
где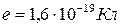 
– заряд электрона; 
– потенциал электростатического поля у поверхности шарика (
– электрическая постоянная).
Таким образом,
,
и уравнение Эйнштейна можно переписать в виде:
,
откуда выразим 
:
.
Наименование: 
.
Вычисление: 
Ответ: максимальный заряд шарика Q max = 107 Кл.
Задача 7.2. Какая доля энергии фотона уносится фотоэлектронами, выбитыми из металла светом с частотой 2×1015 Гц, если красная граница фотоэффекта равна 300 нм?
|
|
|
| Дано: ν = 2∙1015 Гц λ0 = 300 нм = 3·10–7м |
 –?
|
Решение:
При облучении металла светом происходит явление фотоэффекта – выбивание электронов с поверхности металла. При этом энергия падающих на металл фотонов расходуется в соответствии с уравнением фотоэффекта (7.1), согласно которому часть энергии фотона переходит в кинетическую энергию электрона, т.е. доля энергии, уносимой фотоэлектронами будет равна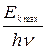 
.
Из (7.1) найдем
Работа выхода электронов из металла равна минимальной энергии фотонов, при которой еще возможен фотоэффект
,
где 
– красная граница фотоэффекта.
Тогда максимальная кинетическая энергия электронов будет равна
.
Доля этой энергии от энергии фотона составит
.
Вычислим: 
.
Ответ: электроны уносят половину энергии фотонов.
Задача 7.3. Построить график зависимости задерживающей разности потенциалов от частоты падающего света для цезия.
Решение:
 .
| (7.2) |
Электроны, выбиваемые фотонами из металла, полностью задерживаются обратным электрическим полем, созданным между электродами фотоэлемента. Изменение кинетической энергии электронов при этом равно работе электрического поля:
При полном торможении
,
а работа тормозящего электрического поля равна
,
где e – заряд электрона; 
– задерживающая разность потенциалов.
Тогда
  ,
| (7.3) |
и уравнение Эйнштейна для фотоэффекта (7.1) примет вид
 .
| (7.4) |
Выразим (7.2) задерживающую разность потенциалов:
 .
| (7.5) |
Уравнение (7.5) представляет собой зависимость задерживающей разности потенциалов от частоты падающего света 
. Это линейная зависимость вида 
, где угловой коэффициент
 ,
| (7.6) |
а свободный член
 .
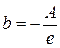| (7.7) |
Для цезия работа выхода электронов из металла равна А = 1,9 эВ ≈ 3∙10–19Дж.
Работа выхода электронов из металла равна минимальной энергии фотонов, при которой еще возможен фотоэффект
 ,
| (7.8) |
где 
– частота, соответствующая красной границе фотоэффекта.
|
|
|
При частоте падающего на металл света, равной , кинетическая энергия фотоэлектронов равна нулю, следовательно, согласно (7.3), в точке ν = ν 0 график будет пересекать ось абсцисс.
Вычислим из (7.8):
(Гц).
Это будет первая точка нашей прямой.
В качестве второй точки можно взять точку пересечения графиком оси ординат на основании (7.7): 
. Однако это будет верно только математически, физически же состояния, характеризуемые зависимостью (7.5) при ν < ν 0 не могут быть реализованы. Поэтому лучше вычислить значение U з при любом произвольном значении частоты падающего света, или провести прямую из точки ν = ν 0 под углом a к оси абсцисс. На основании (7.6) 
. Воспользуемся вторым способом. На рис. 7.1. приведен график зависимости (7.5) в общем виде, значения параметров известны: e = 1,6∙10-19 Кл, h = 6,63∙10–34 Дж∙с, ν 0 = 4,5∙1014 Гц.
8. эффект комптона
Задача 8.1. Под каким углом произошло комптоновское рассеяние фотона рентгеновского излучения на свободном электроне, если в результате этого рассеяния фотон потерял 20% своей энергии? Какая часть энергии фотона перейдет в кинетическую энергию отдачи электрона?
| Дано: Δ W Ф = 0,2 W Ф1 |
φ –?
 –?
|
Решение:
Эффект Комптона состоит в упругом соударении фотона и покоящегося электрона. При этом выполняется закон сохранения импульса:
,
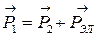где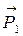 
и 
– импульсы фотона до и после рассеяния соответственно.
Импульсы и энергии фотона до и после рассеяния соответственно равны
, 
, W Ф1 = 
, W Ф2 = 
,
где h – постоянная Планка, с – скорость света.
По условию задачи, потери энергии фотона составляют 20%, т.е. Δ W Ф = 0,2 W Ф1, значит,
W Ф2 = W Ф1 – 0,2 W Ф1 = 0,8 W Ф1,
,
следовательно,
.
Из векторной диаграммы сложения импульсов (рис.8.1) найдем
cos φ = 
,
значит, угол рассеяния фотона равен φ = arсcos 0,8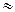 
37°.
При упругом рассеянии выполняется также закон сохранения энергии:
W Ф1 = W Ф2 + W ЭЛ,
где W Ф1 и W Ф2 – энергии фотона до и после рассеяния.
Из закона сохранения энергии следует, что вся энергия, теряемая фотоном при столкновении, переходит в кинетическую энергию электрона, т.е. W ЭЛ = Δ W Ф = 0,2 W Ф1 или = 0,2 = 20%.
Ответ: угол рассеяния фотона φ = 37°, кинетическая энергия электрона отдачи составляет 20% от первоначальной энергии фотона.
|
|
|
9. гипотеза де бройля
Задача 9.1. Найти длину волны де Бройля для протона, кинетическая энергия которого равна энергии теплового движения молекулы водорода при комнатной температуре.
Дано:
W k = W Т(Н2)
|
| λ Б –? |
Решение:
Длина волны де Бройля рассчитывается по формуле:
 ,
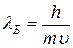| (9.1) |
где 
– постоянная Планка, 
– импульс частицы.
Массу протона возьмем из таблицы: 
.
Скорость протона 
найдем из условия равенства энергий. Кинетическая энергия протона равна:
.
Энергия теплового движения молекулы водорода находится по формуле:
,
где 
– число степеней свободы молекулы, 
– постоянная Больцмана, 
– абсолютная температура.
Молекула водорода – двухатомная, поэтому для нее 
. Комнатную температуру примем 20°С или 293 К.
Приравняем энергии протона и водорода:
,
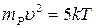отсюда выразим скорость протона:
,
и подставим ее в выражение для длины волны де Бройля (9.1):
или
.
Наименование: 
Вычисление:
Ответ: длина волны де Бройля для протона равна 
.
Задача 9.2. Показать, что стационарным орбитам Бора соответствует целое число волн де Бройля. Сколько длин волн укладывается на каждой орбите? Как зависит длина волны от номера орбиты и универсальных постоянных?
Решение:
Согласно теории водородоподобных атомов Бора, в одноэлектронном ионе электрон может двигаться по круговым орбитам (рис. 4.1), разрешенные радиусы которых r n связаны с линейными скоростями υ n электрона на этих орбитах правилом квантования (4.1). Длина n -ой орбиты равна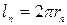 
, разделим ее на длину волны де Бройля (9.1):
,
т.е. на n -ой боровской орбите укладывается n длин волн де Бройля.
Правило квантования (4.1) и второй закон Ньютона для электрона на n -ой орбите (4.5) дают систему уравнений с двумя неизвестными (4.9). Выразим υ n из первого уравнения системы (4.9):
,
и подставим во второе уравнение системы:
.
Теперь упростим и выразим r n:
Отсюда радиус n -ой орбиты электрона равен
.
Тогда длина волны де Бройля будет равна:
.
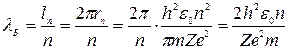Последнее выражение дает зависимость длины волны де Бройля от фундаментальных постоянных.
|
|
|
10. волновая функция
Задача 10.1. Оценить кинетическую энергию протона, локализованного в прямоугольной одномерной потенциальной яме c бесконечно высокими стенками и шириной а = 10-15м (размеры атомного ядра).
Решение:
Состояние частицы в квантовой механике задаётся волновой функцией координат и времени y(x, y, z, t), значения которой в любой точке пространства и в любой момент времени задает уравнение Шредингера. Если функция y не зависит от времени и является функцией только одной координаты l (т.е. в случае плоской волны), то она задается амплитудным (или стационарным) уравнением Шредингера:
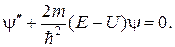
| (10.1) |
В этом уравнении Е – полная энергия частицы, U – потенциальная энергия. При движении протона вдоль оси l его потенциальная энергия меняется так, что в интервале от l = 0 до l = a потенциальная энергия равна нулю, а в остальных точках (l < 0 и l > a) потенциальная энергия частицы бесконечно велика. График такой зависимости потенциальной энергии от координаты l получил название потенциального "ящика" (рис. 10.1).
Квадрат волновой функции определяет собой плотность вероятности – вероятность нахождения частицы в элементарном объеме:
,
для одномерного случая
.
Тогда вероятность встретить частицу в определенном месте пространства определяется квадратом волновой функции:
 .
| (10.2) |
Чтобы частица имела координату l ³ a, она должна получить бесконечно большую энергию U ® ¥. То же самое и для координат l £ 0. Поэтому вероятность встретить частицу за пределами потенциального ящика стремится к нулю, а если так, то согласно (10.1) значение функции y в точках l = a и l = 0 должно стремиться к нулю.
Для частицы в потенциальном ящике уравнение Шрёдингера (10.1) имеет вид:
 .
| (10.3) |
Это дифференциальное уравнение второго порядка с постоянными коэффициентами, и решением его, как известно из курса математики, является гармоническая функция, то есть синус или косинус, а в общем случае – сумма этих функций. Для упрощения записи заменим коэффициент при y:
| (10.4) |
Тогда уравнение (10.3) примет вид
 .
| (10.5) |
Решение этого уравнения ищем в виде
| Y(l) = A sin(kl) + B cos(kl), | (10.6) |
Постоянные коэффициенты А и В найдём из граничных условий, то есть из полученных нами выше значений функции y на границах ящика, при l = 0 и при l = a: y(0) = 0 и y(а) = 0. Подставив в общее решение (10.6) значение l = 0, будем иметь
Y(0) = A sin(0) + B cos(0) = 0,
откуда очевидно, что коэффициент В = 0. С учётом последнего волновая функция будет содержать только синус:
| Y(l) = A sin(kl). | (10.7) |
В соответствии со вторым граничным условием y в точке l = a должна обращаться в нуль:
|
|
|
Y(а) = А sin (ka) = 0.
Отсюда очевидно, что sin (ka) = 0, и аргумент под знаком синуса должен быть кратен p: ka = np, где п – целое число: п = 1, 2, 3,… Следовательно, в волновой функции, определяющей движение частицы в потенциальном ящике, k может принимать не любые, а только фиксированные значения
 ; (n = 1,2,3…).
| (10.8) |
Подставляем полученное выражение (10.8) в формулу замены (10.4):
и выражаем энергию:
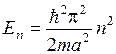
или
 .
| (10.9) |
Еп – кинетическая энергия частицы, находящейся в квантовом состоянии с номером п, т.е. энергия протона, находящегося в потенциальном ящике, квантована. Она кратна минимальной энергии
,
т.е. протон может иметь энергию E 1, 4 E 1, 9 E 1 и так далее (рис. 10.2).
Вычислим минимальную кинетическую энергию протона:
(Дж)
или 
(эВ) или 200 МэВ.
Ответ: минимальная кинетическая энергия протона 200 МэВ.
Задача 10.2. Частица в одномерной потенциальной яме с шириной a с бесконечно высокими стенками находится в состоянии n = 3. Определить вероятность нахождения частицы в области 0 < l < а/3. Построить график зависимости плотности вероятности │ψ2│от координаты x.
Решение:
В этой задаче рассматривается случай, аналогичный рассмотренному в предыдущей задаче. Движение частицы ограничено, и ее потенциальная энергия при движении вдоль оси l меняется таким образом, что график зависимости U (l) имеет вид одномерного прямоугольного “ящика” (рис. 10.1). Энергия частицы в потенциальном “ящике” квантуется, и поведение частицы описывается волновой функцией (10.7). С учетом (10.8) эта функция примет вид
,
где n – номер квантового состояния. В нашем случае (для n = 3)
 .
| (10.10) |
Из (10.2) можно найти вероятность нахождения частицы в заданном интервале координат:
 .
| (10.11) |
Подставим выражение для волновой функции (10.10) в подынтегральное выражение в (10.11) и расставим переделы интегрирования:
 .
| (10.12) |
Найдем 
из условия нормировки:
 ,
| (10.13) |
это означает, что вероятность нахождения частицы в потенциальном ящике равна 1 (т.е. она там есть стопроцентно). В это равенство входит табличный интеграл вида
 ,
| (10.14) |
где, в нашем случае, 
. Подставим значение интеграла (10.14) в условие нормировки (10.13) и, учитывая пределы интегрирования, получим:
,
отсюда
 .
| (10.15) |
С учетом (10.14) и (10.15) сделаем расчет вероятности z по (10.12):
,
т.е. вероятность нахождения частицы в состоянии с n = 3 в первой трети потенциального ящика составляет 1/3.
Для построения графика зависимости 
сначала необходимо построить график функции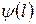 
. Функция (10.10) обращается в ноль, если 
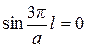. Это происходит при 
, где k – целое число. Значит, синусоида пересекает ось l в точках 
, т.е. 0, а /3, 2 а /3, а. Строим синусоиду 
(рис. 10.2) и преобразуем ее в график функции 
, которая может принимать только положительные значения. Из второго графика видно, что в интервал 0 < l < а/ 3 попадает 1/3 всей площади под графиком функции . Т.к. вся площадь равна вероятности нахождения частицы внутри всего ящика (т.е. 1), убеждаемся, что вероятность нахождения частицы в указанном интервале равна 1/3 (заштрихованная часть площади).
11. соотношение неопределенностей
Задача 11.1. Атом излучает фотон с длиной волны 800 нм. Известно, что время излучения D t составляет 10–8 с. С какой точностью может быть локализован фотон в направлении своего движения? Оценить относительную ошибку Dl/lв определении указанной длины волны, исходя из соотношения неопределенностей для энергии и времени.
| Дано: λ = 800 нм = 8∙10-7 м Δ t = 10–8 с |
| Δ х –? Dl/l –? |
Решение:
Т.к. точно неизвестно, в какой момент времени происходит излучение, то местонахождение фотона также невозможно точно определить. Если известен интервал времени, в котором происходит излучение, то положение фотона можно тоже определить лишь в некотором интервале координат:
Δ x = c ∙Δ t,
где с = 3∙108 м/с – скорость света (скорость распространения фотона).
Вычислим: Δ x = 3∙108∙10–8 = 3 (м).
Чтобы найти Dl/l, воспользуемся соотношением неопределенностей для энергии и времени:
Δ Е ∙Δ t ≥ 
или
,
где ħ =6,63∙10-34Дж∙с – постоянная Планка.
Энергия фотона равна:
,
дифференцируя по λ, найдем d E:
.
Подставляя последнее выражение в соотношение неопределенностей, получим:
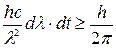
или
.
Отсюда найдем минимальную относительную ошибку в определении длины волны
.
Вычислим:
Ответ: 
м, 
.
Задача 11.2. Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию протона, локализованного в области размером Δ x = 10-15м (размеры атомного ядра), пренебрегая релятивистскими эффектами.
| Дано: Δ x = 10-15м |
| Ekmin –? |
Решение:
Из соотношения неопределенностей координата–импульс
или 
найдем
.
Кинетическая энергия протона в классическом случае равна 
.
Чтобы найти 
, надо найти производную от энергии по скорости:
,
отсюда
или 
.
Значит, 
.
Выразим 
:
.
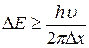Возьмем для оценки максимально возможное значение скорости с = 3∙108 м/с, получим неопределенность в определении энергии частицы:
.
Минимальное значение кинетической энергии не может превышать эту неопределенность, поэтому
(Дж)
или
(эВ) или 200 МэВ.
Ответ: минимальная энергия частицы 200 МэВ.
12. физика ядра
Задача 12.1. Вычислить удельную энергию связи ядра изотопа 4Be8.
Решение:
При образовании ядра часть массы частиц, принимающих участие в этом процессе, идёт на создание энергии связи, которая определяется по формуле Эйнштейна
 Е св = c2 Δ m,
| (12.1) |
где c – скорость света в вакууме, Δ m – дефект масс, который находится как разность суммарной массы нуклонов и массы ядра:
| Δ m = [ ZmР + (A – Z)mN ] – m Я.
| (12.2) |
где тР – масса протона; тN – масса нейтрона; т Я– масса ядра, Z – порядковый номер элемента в таблице Менделеева (он равен заряду ядра и, значит, числу протонов нем), А – массовое число (оно определяет количество нуклонов в ядре), соответственно, (A – Z) – число участвующих в образовании ядра нейтронов.
Удельная энергия связи – это энергия связи, приходящаяся на один нуклон, т.е.
| (12.3) |
В периодической таблице элементов (и в таблицах масс изотопов) приводятся массы атомов, а не ядер. Поэтому нужно учесть, что масса атома отличается от массы ядра на массу всех электронов, которых в атоме столько же, сколько протонов в ядре (это обеспечивает электрическую нейтральность атома). Поэтому массу ядра можно найти так:
| m Я = m А – Z m е.
| (12.4) |
Подставим (12.4) в формулу для дефекта масс (12.2) и перегруппируем слагаемые:
Δ m = [ ZmР + (A – Z)mN ]– [ m А – Z m е] = Z (mР + +m е) + (A – Z)mN – m А
| Δ m = Z m (1Н1) + (A – Z)mN – m А. | (12.5) |
Здесь мы обозначили m (1Н1) = mР + m е – масса атома водорода, которую также, как и массу рассматриваемого изотопа, возьмем из таблицы.
Теперь выпишем все необходимые данные из таблиц:
mР = 1,00728 а.е.м.;
mN = 1,00867 а.е.м.;
m (1Н1) = 1,00783 а.е.м.;
mА = m (4Be8) = 8,00531 а.е.м.;
1 а.е.м. = 1,6605655·10-27 кг;
c = 2,9979·108 м/с.
Для изотопа бериллия 4Be8 определяем, что Z = 4, A = 8.
Подставляем все эти данные в выражение для дефекта масс (12.5):
Δ m = 4· 1,00783 + 4·1,00867 – 8,00531 = 0,06069 (а.е.м.)
Переведем полученное значение в килограммы:
Δ m = 0,06069 · 1,6605655·10-27 = 0,10078·10-27 = 1,0078·10-28 (кг).
Теперь вычислим энергию связи по (13.1):
Е св = (2,9979·108) 2 · 1,0078·10-28 = 9,0575·10–12 (Дж)
Переведем полученное значение в электрон-вольты:
1 эВ = 1,6·10–19 Дж
Е св = 
= 5,66·107 (эВ) или Е св = 56,6 МэВ.
Тогда, согласно (12.3), на один нуклон в ядре приходится энергия
МэВ.
Ответ: удельная энергия связи ядра изотопа бериллия 4Be8 равна 7,08 МэВ.
Задача 12.2. Определить возраст древних деревянных предметов, если известно, что удельная активность изотопа С 14 у них составляет 3/5 удельной активности этого изотопа в только что срубленных деревьях. Период полураспада ядер С 14 равен 5570 лет.
Дано:
T = 5570 лет
|
| t –? |
Решение:
Известно, что деревья поглощают углекислый газ, преобразуя его в углерод и кислород. В состав углекислого газа (СО2) помимо углерода С12 в небольшом количестве входит изотоп С14. Когда дерево срубают, оно перестает поглощать СО2, и количество углерода в нем больше не увеличивается. Изотоп углерода С14 радиоактивен, и со временем его количество уменьшается в результате распада. По оставшемуся количеству С14 в деревянных изделиях определяют их возраст.
Активность изотопа определяет количество распадающихся ядер в единицу времени:
или 
,
где N – количество наличных ядер, 
– постоянная распад а, Т – период полураспада.
Удельная активность – это активность единицы массы изделия, т.е.
,
а в только что срубленных деревьях
.
Запишем закон распада в интегральном виде (предполагая, что возраст деревянных изделий соизмерим с периодом полураспада):
или
,
где N – количество наличных ядер, N 0 – исходное количество ядер.
Левую часть этого равенства, пренебрегая изменением массы деревянного изделия, можно заменить на отношение удельных активностей:
или
.
Потенцируя последнее выражение, находим время t, за которое произошло такое уменьшение активности, – возраст деревянных предметов:
.
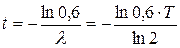Вычислим:
(лет).
Ответ: деревянным предметам 4107 лет.
Задача 12.3. В урановой руде обнаружен 82 Рb 206. Чему равен возраст урановой руды, если она теперь содержит 0,8 г свинца на каждый грамм 92 U 238?
| Дано: m(92U238) = 1 г = 10–3 кг m(82Pb206) = 0,8 г = 0,8∙10–3 кг |
| t –? |
Решение:
Каждое ядро атома свинца образуется из ядра атома урана в результате нескольких ядерных реакций распада. Уран, содержащийся в руде, распадается все время существования руды, при этом количество урана в руде уменьшается, а количество свинца растет. В некоторый момент времени t на N ядер урана приходится Δ N ядер свинца, т.е. распавшихся ядер урана. Распишем число ядер через массу (считаем, что масса ядра практически равна массе атома):
, 
.
Полагая, что возраст урановой руды соизмерим с периодом полураспада урана, запишем закон распада в интегральном виде:
,
где N – количество наличных ядер, N 0 – исходное количество ядер, – постоянная распада, Т – период полураспада урана (из справочной таблицы Т(92U238) = 4,5∙109 лет).
Исходное количество ядер N 0 = N + Δ N, тогда закон распада примет вид:
или
.
Потенцируя последнее выражение, получаем:
или
.
Подставим выражения для N и Δ N и выразим время:
.
Молярные массы урана и свинца равны:
μ (92U238) = 0,238 кг/моль, μ (82Pb206) = 0,206 кг/моль.
Вычисление:
(лет).
Ответ: возраст урановой руды составляет 4,25∙109 лет.
Библиографический список
1. Чертов, А.Г. Задачник по физике // А.Г. Чертов, А.А. Воробьёв. – М.: Высшая школа, 1993.
2. Волькенштейн, В.С. Сборник задач по общему курсу физики / В.С. Волькенштейн. – М.:Физматгиз, 1996.
3. Фирганг, Е.В. Руководство к решению задач по курсу общей физики: Учебное пособие для втузов / Е.В. Фирганг. – М.:Высшая школа, 1987.
4. Трофимова, Т.И. Курс физики: Учебное пособие для вузов / Т.И. Трофимова. – М.: Высшая школа, 2001.
5. Савельев, И.В. Курс общей физики / И.В. Савельев. – М.:Наука, 1987. – Т.2.
6. Соколова, Н.М. Физика: Курс лекций. / Н.М. Соколова, В.И. Биглер. – Челябинск: Изд. ЮУрГУ, 2001. – Ч. 2.
ПРИЛОЖЕНИЯ
Приложение 1
Фундаментальные физические константы
(с точностью, требуемой для решения задач)
| Название | Обозначение | Величина |
| Гравитационная постоянная | G | 6,67×10–11 
|
| Скорость света в вакууме | c | 3×108 
|
| Магнитная постоянная | m0 | 4p×10-7 
|
| Электрическая постоянная | e0 | 8,85×10-12 
|
| Постоянная Планка | h | 6,63×10-34 Дж×с |
| Постоянная Планка | ħ | 1,05×10-34 Дж×с |
| Масса покоя электрона | m e | 9,1×10–31 кг |
| Масса покоя протона | m p | 1,6726485×10–27 кг |
| Масса покоя нейтрона | m n | 1,6749543×10–27 кг |
| Отношение массы протона к массе электрона | 
| |
| Элементарный заряд | e | 1,6×10-19 Кл |
| Отношение заряда электрона к его массе | 
| 1,76×1011 
|
| Атомная единица массы | 1 а.е.м. | 1,6605655×10–27 кг |
| Постоянная Авогадро | N A | 6,02×1023 моль–1 |
| Универсальная газовая постоянная | R | 8,31 
|
| Постоянная Больцмана | k | 1,38×10-23 
|
| Постоянная Стефана – Больцмана | s | 5,67×10-8 
|
| Постоянная Ридберга | R | 1,097×107 м-1 |
Приложение 2
|
|
|
