 |
Перечень контрольных заданий для студентов профиля подготовки «Информатика и вычислительная техника» профилизации «Компьютерные технологии»
|
|
|
|
Таблица 1. Полный срок обучения
| 1 семестр | 2 семестр | 3 семестр | |
| Контр. раб.1 | Контр. раб.2 | Контр. раб.3 | |
| Номера заданий | 11-20 | 281-290 | 461-470 |
| 51-60 | 301-310 | 321-330 | |
| 91-100 | 231-240 | 341-350 | |
| 111-120 | 261-270 | 521-530 | |
| 141-150 | 421-430 | 541-550 | |
| 191-200 | 431-440 | ||
| 441-450 |
Таблица 2. Сокращённый срок обучения
| 1 семестр | 2 семестр | |
| Контр. раб.1 | Контр. раб.2 | |
| Номера заданий | 11-20 | 231-240 |
| 51-60 | 261-270 | |
| 111-120 | 421-430 | |
| 141-150 | 431-440 | |
| 191-200 | 461-470 | |
| 281-290 | 321-330 | |
| 341-350 | ||
| 521-530 | ||
| 541-550 |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ ЗАДАНИЙ
Задание 11 – 20
Для решения задач 11 – 20 рекомендуется учебное пособие
Данко П.Е., Кожевникова Т.Я. Высшая математика в упражнениях и задачах.
Ч.1. М.: Оникс 21 век. 2005. Гл. I –IV, стр.39 – 91.
Рассмотрим решение аналогичной задачи, взяв координаты вершины пирамиды SABC: А(-3;0;0); В(0;2;0); С(0;0;6); S(-3;4;5).
1) Длину ребра АВ находим по формуле:
2) Угол между рёбрами 
найдём по формуле косинуса угла между векторами 
, координаты которых определяются так:
α
φ
Для решения задания 3) целесообразно решить задачу 7). Уравнение плоскости 
составим по уравнению
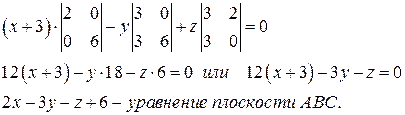
Нормальный вектор этой плоскости
4) Площадь 
определяем с помощью векторного произведения:
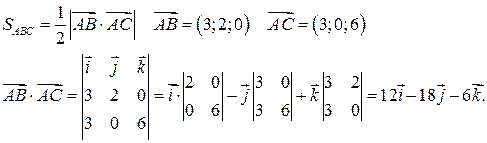
5) Объём пирамиды 
находится через вычисление смешанного произведения векторов 
Изучите понятие смешанного произведения, формулу объёма пирамиды и формулу для вычисления смешанного произведения трёх векторов. Решите самостоятельно.
6) Уравнение прямой 
Канонические уравнения прямой, вектор 
направляющий вектор прямой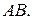 
8) Для определения проекции вершины 
на плоскость выполняютсяследующие действия:
|
|
|
а) составляется уравнение высоты пирамиды 
.
б) находится точка пересечения высоты и основания решением системы, содержащей уравнение высоты и уравнение плоскости.
Решение: вектор 
удобнее взять 
Он будет направляющим для 
По уравнению 
вершина , т.е. 
.
Система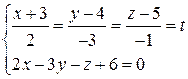 
решается подстановкой
Подставив во второе уравнение, найдём значение 
, а следовательно значения
Точка 
- проекция точки на плоскость 
9) Длину высоты пирамиды можно найти по формуле 
или по формуле расстояния от точки до плоскости – наиболее удобно.
Изучите формулы самостоятельно, решив задание 9).
Задание 51 – 60
Дана система линейных уравнений
Решить систему а) матричным методом, б) методом Крамера, в) методом Гаусса.
а) данной системе соответствует матричное уравнение 
, которое решается по формуле: 
. Матрицы имеют вид:
Находим обратную матрицу
Находим матрицу 
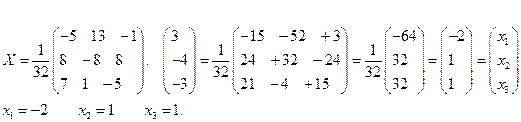
б) 
- формулы Крамера. Вычислим все определители 
в) Метод Гаусса.
Составим расширенную матрицу 
и преобразуем её с помощью элементарных преобразований.
Из полученной матрицы, выделяя последнюю строку, видим, что исключены неизвестные 
и 
. Найдём 
. 
.
Вторая строка соответствует уравнению:
или 
Аналогично из первой строки напишем уравнение:
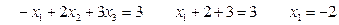
Итак: 
Задание 91 – 100.
Дано комплексное число 
Записать число 
в геометрической и тригонометрической формах и найти все корни уравнения 
Рекомендуемая литература: Данко П.Е., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, ч. II, гл.III, §7, стр.97 – 101.
Найдём алгебраическую форму комплексного числа
Тригонометрическая форма комплексного числа 
определится по формуле 
.
Изобразив число на плоскости, найдём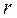 
и 
.
-1 
Итак, число 
Найдём корни уравнения 
вычислим по формуле Муавра
Задание 111 – 120
Вычислить пределы:
а) 
За скобку выносили наивысшую степень 
для числителя и знаменателя.
|
|
|
б) 
Для исключения неопределённости 
требуется числитель и знаменатель разложить на множители.
в) 
В данном случае для исключения неопределённости использованы эквивалентные бесконечно малые,например 
г) Числитель и знаменатель умножаем на выражение, сопряжённое числителю
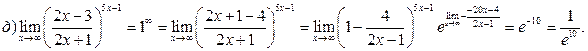
Задание 141– 150
Найти производные 
следующих функций:
а)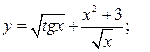 
б) 
;
в) 
г) 
;
д) 
.
б) 
в) 
г) 
Прологарифмируем обе части равенства
Продифференцируем обе части равенства
д) 
Функция 
задана неявно. Учитываем, что 
аргумент, 
функция.
Задание 151 – 160
Найти 
функций:
Решение:
а) 
б) 
Задание 191 – 200
Исследовать методами дифференциального исчисления функцию и построить её график.
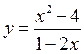
Рассмотрим свойства функции:
1. Область определения: 
2. Чётностьь, нечётность функции: 
Функция общего вида.
3. Асимптоты.
а) Так как 
, то прямая 
является вертикальной асимптотой:
б) 
– наклонная асимптота.
Найдём 
Найдём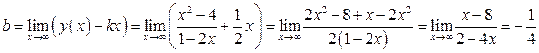 
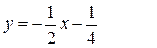– уравнение наклонной асимптоты.
4. Найдём точки экстремума и интервалы монотонности функции:
Так как 
то действительных корней нет, значит, нет точек экстремума.
Производная 
на всей области определения, значит функция
убывает.
5. Точки пересечения с координатными осями
а) с осью 
при 
,
б) с осью 
при 
.
Используя исследование функции, строим график (схематично).
Задания 141-150, 151-160, 191-200 легко выполнить, используя учебное пособие П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах ч.I гл. VII §§ 1-2 стр. 151-183.
Задание 231-240
Показать, что функция 
удовлетворяет равенству:
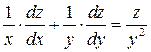
Находим частные производные по 
и по 
:
Подставим в равенство частные производные.
;
Равенство верно.
Задание 251-260
Найти наименьшее и наибольшее значения функции 
в области
 |
y
В С
D
А D
0 1 2 x
а) Найдём стационарные точки
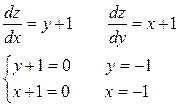
Точка 
- стационарная, но не принадлежит области D.
б) Исследуем данную функцию на границах квадрата АВСD
АВ:
Функция возрастает на границе АВ 
ВС: 
На границе ВС функция возрастает 
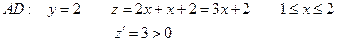
Значит на границе 
фнкция возрастает 
Значит на границе фнкция возрастает 
|
|
|
Найденные значения z сравним и выделяем
Задание 261 – 270
Дана функция 
точка 
и вектор 
Найти 
в точке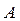 
и производную в точке 
по направлению вектора 
.
Найдём частные производные и вычислим их значение в точке .
– направляющие косинусы вектора 
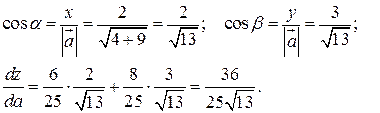
Литература к заданиям 231 – 240, 251 – 260, 261 – 270 – П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова Высшая математика в упражнениях и задачах
гл. VIII §§1-2, §4.
Задание 281 – 290
Найти неопределённые интегралы, выполнив проверку дифференцированием в первых двух примерах.
Решение:
Проверка:
Метод интегрирования по частям для функции 
Формула: 
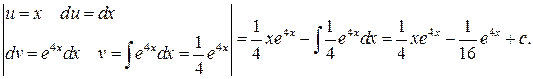
Проверка:
Найдём коэффициенты
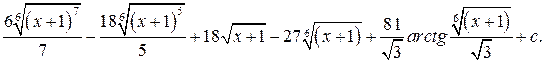
Задания 301– 310
Вычислить несобственный интеграл
Несобственный интеграл расходится.
Методы интегрирования рассматриваются в учебном пособии
– П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова Высшая математика в упражнениях и задачах ч. I, гл. IХ. §§1-4.
Задание 321 – 330
В данном задании предлагается решить дифференциальное уравнение одного из трёх типов – однородное, линейное или с разделяющимися переменными. Предлагается решение однородного уравнения
Найти общее решение дифференциального уравнения первого порядка.
.
Уравнение является однородным.
Функции 
однородные второго порядка.
Уравнение можно привести к виду
разделить обе части на 
а затем на 
.
Введём подстановку
Разделяем переменные:
Интегрируем обе части, получаем
Общее решение примет вид
Задание 341-350
Найти общее и частное решения дифференциального уравнения
при начальных условиях 
.
Однородное уравнение
имеет характеристическое уравнение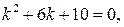 
корни которого 
.
Тогда общее решение 
- для однородного уравнения
Согласно теории общее решение данного неоднородного уравнения имеет вид 
частное решение данного уравнения, правя часть которого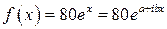 
Учитывая стандартную формулу правой части, находим 
Число 
не совпадает с 
подбираем с учётом этого 
Найдём 
Общее решение данного уравнения
|
|
|
Найдём частное решение, взяв 
для отыскания 
В равенства (1) и (2) подставим начальные условия: 
, тогда
Тема «Обыкновенные дифференциальные уравнения» рассмотрена в пособии П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова Высшая математика в упражнениях и задачах ч. 
, гл.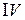 
,
Задание 391-400
Вычислить криволинейный интеграл по дуге 
линии, заданной параметрически
Тогда 
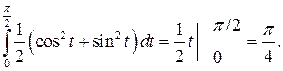
Задание 421-430
Исследовать сходимость числового ряда
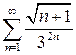
Для исследования данного ряда применяем признак Даламбера:
· 
, ряд расходящийся, 
сходящийся, 
нет ответа по данному признаку.
по данному условию, составим
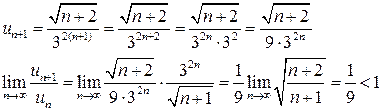
Значит данный ряд сходящийся.
Задание 431-440
Найти область сходимости степенного ряда
Прежде всего определяется радиус сходимости степенного ряда
Значит интервал сходимости 
На границах интервала рассматриваются числовые ряды.
При 
Так как предел 
то ряд расходится.
При 
–знакочередующийся ряд.
1. Рассмотрим члены ряда по абсолютной величине
Члены ряда возрастают, значит по теореме Лейбница при 
ряд расходящийся.
Задание 441 – 450
Вычислить определённый интеграл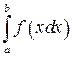 
с точностью 0,001, 
Разложим подынтегральную функцию в ряд, а затем проинтегрируем её почленно.
.
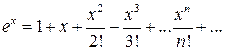
Используя разложение в ряд Маклорена функции
, запишем разложение
Проинтегрировав, получим:
Значение интеграла (по теореме Лейбница) соответствует сумме с точностью 0,001.
Шестое слагаемое, 
поэтому взято пять слагаемых.
Типовые задачи по теме «Ряды» рассматриваются в учебном пособии П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах, ч. 
, гл. 
,§§1-6.
Задание 451 – 460.
Найти три первых отличных от нуля члена разложения в степенной ряд решения 
дифференциального уравнения 
удовлетворяющего данному условию 
Используем разложение искомой функции в ряд Тейлора около точки 
.
В нашем примере 
т.е. первый член ряда обращается в ноль.
Из заданного дифференциального уравнения
Поэтому второй член ряда имеет вид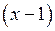 
. Чтобы найти третий член ряда продифференцируем обе части нашего уравнения
И поэтому следующий член ряда равен 
. Аналогично
Третий ненулевой член ряда
Окончательно:
Интегрирование дифференциальных уравнений с помощью рядов рассматривается в учебном пособии П.Е.Данко, А.Г.Попов, Т.М.Кожевникова. Высшая математика в упражнениях и задачах, ч. 
гл. 
, §4.
Задание 461 – 470
Разложить данную функцию 
в ряд Фурье в интервале 
Рядом Фурье периодической функции 
с периодом 
, определённой на сегменте 
называется ряд
где (1)
|
|
|
В случае, когда 
чётная функция, её ряд Фурье содержит только свободный член и косинусы, т.е.
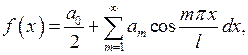
В случае, когда нечётная функция, её ряд Фурье содержит только синусы, т.е.
Если ряд (1) сходится то его сумма 
есть периодическая функция с периодом 
Теорема Дирихле. Пусть функция на сегменте 
имеет конечное число экстремумов и является непрерывной за исключением конечного числа точек разрыва 
рода. Тогда ряд Фурье этой функции сходится в каждой точке сегмента и сумма этого ряда:
1) 
во всех точках непрерывности функции , лежащих внутри сегмента ;
2) 
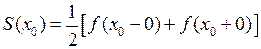, где 
- точка разрыва I рода функции ;
3) 
на концах промежутка, т.е. при 
Разложить в ряд Фурье функцию , заданную в интервале 
уравнением 
.
Графиком этой функции в интервале является отрезок, соединяющий точки 
Сумма ряда Фурье является периодической функцией с периодом 
и совпадает с функцией в интервале .
Определяем коэффициенты ряда Фурье. Сначала находим
Второй интеграл равен нулю как интеграл от нечётной функции, взятый по интервалу, симметричному относительно начала координат. Таким образом,
Далее, находим коэффициенты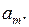 
Имеем
Нетрудно видеть, что оба интеграла равны нулю (подъинтегральная функция второго интеграла является нечётной как произведение чётной функции на нечётную). Итак, 
Найдём теперь коэффициенты 
Первый интеграл равен нулю. Подъинтегральная функция второго интеграла является чётной как произведение двух нечётных функций. Таким образом,
Интегрируя по частям, получим 
Следовательно, разложение функции в ряд Фурье имеет вид:
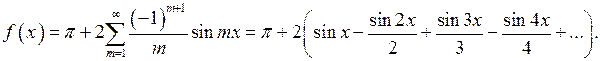
Ряды Фурье рассматриваются в учебном пособии П.Е.Данко, А.Г.Попов, Т.М.Кожевникова. Высшая математика в упражнениях и задачах, ч. гл. 3, §8.
Задание 481 – 491.
Представить 
где 
в виде 
; проверить, является ли она аналитической. Если да, то найти значение её производной в заданной точке 
Здесь мы воспользовались формулой Эйлера 
Необходимыми условиями дифференцируемости функции 
в точке 
являются условия Коши – Римана
Находим частные производные
Т.е. условия Коши – Римана выполнены во всех точках комплексной плоскости. Кроме того, частные производные непрерывны всюду. Следовательно, заданная функция дифференцируема и является аналитической на всей комплексной плоскости.
Производная может быть найдена по тем же формулам, что для функций действительного переменного.
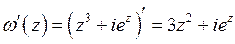
В заданной точке 
Типовые задачи по теме «Производная функции комплексного переменного» рассматривается в учебном пособии П.Е.Данко, А.Г.Попов, Т.М.Кожевникова. Высшая математика в упражнениях и задачах, ч. гл.VII, §§1,2.
Задание 491 – 500.
Используя теорему о вычетах, вычислить заданный интеграл по замкнутому контуру С, обходимому против часовой стрелки.
Основные определения и теорема.
Точка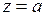 
называется полюсом к-того порядка функции 
, если 
Пусть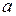 
– полюс n-го порядка функции . Вычет функции относительно её полюса n-го порядка вычисляется по формуле
(residue– вычет).
Если 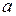– полюс первого порядка (простой полюс) функции , то
Пусть – аналитическая функция в замкнутой области 
, кроме конечного числа изолированных особых точек 
(полюсов или существенно особых точек). Тогда интеграл от функции по контуру 
, содержащему внутри себя эти точки и целиком лежащему в области , равен произведению 
на сумму вычетов в указанных особых точках, т.е.
.
(Основная теорема о вычетах).
Пример:
Найти 
Где 
– окружность, 
,полюс ы i, – i, 2 находятся внутри замкнутого контура .
Отсюда
Типовые задачи по теме «Применение вычетов к вычислению интегралов» рассматривается в учебном пособии П.Е.Данко, А.Г.Попов, Т.М.Кожевникова. Высшая математика в упражнениях и задачах, ч. гл.VII, §6.
Задание 501 – 510.
Найти оригинал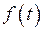 
, которому соответствует изображение Лапласа 
.
Если изобра
|
|
|
