 |
Метод конечных элементов в высокоскоростных динамических процессах
|
|
|
|
к.т.н., доцент С.А. Куканов,
А.В. Полянсков, М.С. Баранов
Разработка бронежилетов, с которыми взаимодействуют поражающие элементы с различными скоростями, сопряжена с необходимостью учитывать такие факторы, влияющие на защищенность живой силы, как физико-механические свойства каждого элемента бронезащиты (БЖ). Учет влияния геометрических размеров элементов конструкции БЖ, необходимо использовать как дополнительный управляющий процессом фактор. Воздействие поражающего элемента на живую силу в БЖ представляет процесс ударно-волнового взаимодействия, а задача предварительного выбора оптимальных размеров элементов БЖ на этапе проектирования и оценки стойкости средств индивидуальной бронезащиты требует более глубокого исследования.
Анализ предшествующих теоретических наработок в области решения задач моделирования процесса взаимодействия различных поражающих элементов с БЖ и экспериментальные исследования показали, что данные методики не обеспечивают в полной мере необходимым инструментом анализа уровня. Данная задача может быть решена только при наличии адекватного методического аппарата оценки стойкости БЖ, используемого на этапе проектирования изделия.
При моделировании процесса высокоскоростного взаимодействия, позволяющем оценивать стойкость экипировки, использовали метод конечных элементов.[2.с.225;] Метод конечных элементов, базирующийся на основных уравнениях механики сплошных сред, основан на использовании теории прочностного анализа. Прочностной динамический анализ используется для определения действия на конструкцию или ее составные части нагрузок, зависящих от времени. В отличие от статических расчетов в этом типе анализа принимаются во внимание рассеяние энергии и инерционные эффекты переменных во времени нагрузок. Примерами таких нагрузок являются:
|
|
|
- циклические нагрузки (вращающиеся части оборудования);
- внезапно прикладываемые нагрузки (удар или взрыв);
- случайные нагрузки;
- любые другие переменные нагрузки, типа движущихся нагрузок на мосты.
В программе ANSYS [1.с.568;] все виды динамического анализа основываются на следующем общем уравнении движения в конечно-элементной форме:
[ M ] { u '' } + [ C ] { u ' } + [ K ] { u } = { F (t)}, (1)
где [ M ] - матрица масс;
[ C ] - матрица сопротивлений;
[ K ] - матрица жесткостей;
{ u'' } - вектор узловых ускорений;
{ u' } - вектор узловых скоростей;
{ u } - вектор узловых перемещений;
{ F } - вектор нагрузок;
(t) - время.
С помощью этого уравнения определяются значения неизвестных {u}, которые в любой момент времени удовлетворяют условиям равновесия системы при наличии сил инерции и рассеяния энергии.
Программа ANSYS способна выполнять следующие виды динамических расчетов: динамика переходных процессов, модальный анализ, отклик на гармоническое воздействие, спектральный анализ и отклик на случайную вибрацию. [1.с.439;]
Анализ переходных процессов (неустановившихся режимов) применяется для определения параметров динамического поведения конструкций, которые подвергаются действию нагрузок, произвольно меняющихся во времени. [2.с.123;]
Выходные величины полученного решения (в виде узловых перемещений, деформаций, напряжений, усилий и т.п.) представляют собой функции времени. Каждую из этих величин можно вывести на экран в виде графика зависимости от времени или некоторой другой переменной с помощью постпроцессора истории нагружения. [3.с.318; Постпроцессор общего назначения позволяет просмотреть результаты анализа переходного процесса для любого момента времени (например, показать картину напряженно-деформированного состояния).
|
|
|
Целью моделирования являлось определение кинематических параметров поражающего элемента, а также стойкости, характера механизмов поведения и разрушения элементов БЖ. Математическое моделирование выполнено в программном комплексе ANSYS.[1.с.89;] Модель взаимодействия поражающего элемента с элементами БЖ представлена в виде пространственной совокупности объемных элементов, работающих в условиях динамического нагружения. Выбран объемный восьмиузловой конечный элемент, который позволил провести моделирование без искривления границ поражающего элемента и БЖ и точно отобразить их геометрические размеры. Вид сбоку конечно-элементных моделей поражающего элемента и элементов БЖ на рис.1.
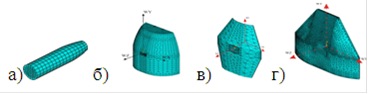
Рис.1. Конечно-элементные модели: а - сердечник 7,62-мм пули ЛПС; б - биообъект; в - тканевый пакет; г - бронепанель.
Решена задача моделирования взаимодействия пули с различными элементами БЖ, которая позволяет учитывать образование импульсного давления. Получен результат решения математического моделирования, который дает возможность оценивать стойкость БЖ и такие параметры заброневой, контузионной травмы, как импульсное давление, глубину внедрения пули и кинематические параметры, возникающие при ударно-волновом нагружении в имитаторе биообъекта. Результат изменения перемещения, скорости и ускорения пули по времени показан на рис.2.
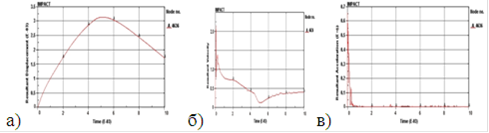
Рис. 2. Зависимость от времени: а - перемещения; б - скорости; в - ускорения
В результате математического моделирования определили характер разрушения пули и БЖ. Характер разрушения БЖ и пули ЛПС в различные моменты времени показан на рис.3.

t=0,59 *10-3 c t=0,99 *10-3 c t=2,66 *10-3 c t=7,361 *10-3 c
Рис. 3. Характер разрушения 7,62-мм пули ЛПС и элементов БЖ 6Б12-2
Таким образом, все типы расчетов, выполняемые программой ANSYS, основаны на классических инженерных представлениях и концепциях. При помощи надежных численных методов эти концепции могут быть сформулированы в виде матричных уравнений, которые наиболее пригодны для конечно-элементных приложений. Совокупность дискретных областей (элементов), связанных между собой в конечном числе точек (узлов), представляет собой математическую модель системы, поведение которой нужно анализировать. Основными неизвестным являются степени свободы узлов конечно-элементной модели. К степеням свободы относятся перемещения, повороты, температуры, давления, скорости, потенциалы электрических или магнитных полей; их конкретное содержание определяется типом элемента, который связан с данным узлом. В соответствии со степенями свободы для каждого элемента модели формируются матрицы масс, жесткости (или теплопроводности) и сопротивления (или удельной теплоемкости). Эти матрицы приводят к системам совместных уравнений, которые обрабатываются так называемыми «решателями». Решение задачи математического моделирования взаимодействия пули с элементами БЖ, позволило получить результат по оценке его стойкости.
|
|
|
Библиографический список
1. Hallquist J. O. LS-DYNA Theoretical Manual. Livermore Software Technology Corporation. - California. 1998.
2. Селиванов В.В. Механика разрушения деформируемого тела. - Москва: Издательство МГТУ им. Н.Э. Баумана.2006.419 с.
. Партон В.З., Морозов Е.М. Механика упругопластического разрушения. Основы механики разрушения. - Москва: Издательство УРСС. 2008.352 с.
|
|
|


