 |
Найти коэффициент эластичности для указанной модели в заданной точке X. Сделать экономический анализ.
|
|
|
|
КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ
КОНТРОЛЬНАЯ РАБОТА
ПО ДИСЦИПЛИНЕ
«ЭКОНОМЕТРИКА»
2007
Задания к контрольной работе:
1. Метод наименьших квадратов для однофакторной линейной регрессии
2. Найти коэффициент эластичности для указанной модели в заданной точке X. Сделать экономический анализ.
Модель: Y = (2/X) + 5; X = 0;
3. Убыточность выращивания овощей в сельскохозяйственных предприятиях и уровни факторов (сбор овощей с 1 га, ц и затраты труда, человеко-часов на 1 ц), ее формирующих, характеризуются следующими данными за год:
| № района | Фактор | Уровень убыточности, % | |
| Сбор овощей с 1 га, ц | Затраты труда, человеко-часов на 1 ц | ||
| 1 | 93,2 | 2,3 | 8,8 |
| 2 | 65,9 | 26,8 | 39,4 |
| 3 | 44,6 | 22,8 | 26,2 |
| 4 | 18,7 | 56,6 | 78,8 |
| 5 | 64,6 | 16,4 | 34 |
| 6 | 25,6 | 26,5 | 47,6 |
| 7 | 47,2 | 26 | 43,7 |
| 8 | 48,2 | 12,4 | 23,6 |
| 9 | 64,1 | 10 | 19,9 |
| 10 | 30,3 | 41,7 | 50 |
| 11 | 28,4 | 47,9 | 63,1 |
| 12 | 47,8 | 32,4 | 44,2 |
| 13 | 101,3 | 20,2 | 11,2 |
| 14 | 31,4 | 39,6 | 52,8 |
| 15 | 67,6 | 18,4 | 20,2 |
Нелинейную зависимость принять 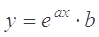
Метод наименьших квадратов для однофакторной линейной регрессии
Линейная регрессия находит широкое применение в эконометрике в виде четкой эконометрической интерпретации ее параметров. Линейная регрессия сводится к нахождению уравнения вида:
Ŷ = а + bx или Ŷ = a + bx + ε;
Уравнение вида Ŷ = а + bx позволяет по заданным значениям фактора x иметь теоретические значения результативного признака, подставляя в него фактические значения фактора X. На графике теоретические значения представляют линию регрессии.

|
Рисунок 1 – Графическая оценка параметров линейной регрессии
Построение линейной регрессии сводится к оценке ее параметров – а и b. Оценки параметров линейной регрессии могут быть найдены разными методами. Можно обратится к полю корреляции и, выбрав на графике две точки, провести через них прямую линию. Далее по графику можно определить значения параметров. Параметр a определим как точку пересечения линии регрессии с осью OY, а параметр b оценим, исходя из угла наклона линии регрессии, как dy/dx, где dy – приращение результата y, а dx – приращение фактора x, т.е. Ŷ = а + bx.
|
|
|
Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов(МНК).
МНК позволяет получить такие оценки параметров a и b, при которых сумма квадратов отклонений фактических значений результативного признака (y) от расчетных (теоретических) минимальна:
∑(Yi – Ŷ xi)2 → min
Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной.
εi = Yi – Ŷ xi.
следовательно ∑εi2 → min
 | |||
| |||
|
Чтобы найти минимум функции, надо вычислить частные производные по каждому из параметров a и b и приравнять их к нулю.
Обозначим ∑εi2 через S, тогда
S = ∑ (Y –Ŷ xi)2 =∑(Y-a-bx)2;
Дифференцируем данное выражение, решаем систему нормальных уравнений, получаем следующую формулу расчета оценки параметра b:
b = (ух – у•x)/(x2-x2).
Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Например, если в функции издержек Ŷ = 3000 + 2x (где x – количество единиц продукции, у – издержки, тыс. грн.) с увеличением объема продукции на 1 ед. издержки производства возрастают в среднем на 2 тыс. грн., т.е. дополнительный прирост продукции на ед. потребует увеличения затрат в среднем на 2 тыс. грн.
|
|
|
Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение регрессии достаточно распространенным в эконометрических исследованиях.
Найти коэффициент эластичности для указанной модели в заданной точке X. Сделать экономический анализ.
Модель: Y = (2/ X) + 5; X = 0;
Известно, что коэффициент эластичности показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%. Формула расчета коэффициента эластичности:
Э = f′(x) X/Y,
где f′(x) – первая производная, характеризующая соотношение прироста результата и фактора для соответствующей формы связи.
Y = (2/X) + 5,
f′(x) = -2/x2;
Следовательно получим следующее математическое выражение
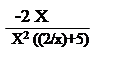 |
| |||

|
При заданном значении X = 0 получим, что коэффициент эластичности равен Э = -1.
Допустим, что заданная функция Y = (2/X) + 5 определяет зависимость спроса от цены. В этом случае с ростом цены на 1% спрос снижается в среднем на 1%.
3. Убыточность выращивания овощей в сельскохозяйственных предприятиях и уровни факторов (сбор овощей с 1 га, ц и затраты труда, человеко-часов на 1 ц), ее формирующих, характеризуются следующими данными за год:
| № района | Уровень убыточности, % | ||
| Сбор овощей с 1 га, ц | Затраты труда, человеко-часов на 1 ц | ||
| 1 | 93,2 | 2,3 | 8,8 |
| 2 | 65,9 | 26,8 | 39,4 |
| 3 | 44,6 | 22,8 | 26,2 |
| 4 | 18,7 | 56,6 | 78,8 |
| 5 | 64,6 | 16,4 | 34 |
| 6 | 25,6 | 26,5 | 47,6 |
| 7 | 47,2 | 26 | 43,7 |
| 8 | 48,2 | 12,4 | 23,6 |
| 9 | 64,1 | 10 | 19,9 |
| 10 | 30,3 | 41,7 | 50 |
| 11 | 28,4 | 47,9 | 63,1 |
| 12 | 47,8 | 32,4 | 44,2 |
| 13 | 101,3 | 20,2 | 11,2 |
| 14 | 31,4 | 39,6 | 52,8 |
| 15 | 67,6 | 18,4 | 20,2 |
Нелинейную зависимость принять 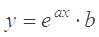
Задание №1
Построим линейную зависимость показателя от первого фактора.
Обозначим: сбор овощей с 1 Га как X1, а уровень убыточности как Y.
| Сбор овощей с 1 га, ц | Уровень убыточности, % |
| X1 | Y |
| 93,2 | 8,8 |
| 65,9 | 39,4 |
| 44,6 | 26,2 |
| 18,7 | 78,8 |
| 64,6 | 34 |
| 25,6 | 47,6 |
| 47,2 | 43,7 |
| 48,2 | 23,6 |
| 64,1 | 19,9 |
| 30,3 | 50 |
| 28,4 | 63,1 |
| 47,8 | 44,2 |
| 101,3 | 11,2 |
| 31,4 | 52,8 |
| 67,6 | 20,2 |
Найдем основные числовые характеристики.
1. Объем выборки n = 15 – суммарное число наблюдений.
2. Минимальное значение величины сбора овощей Х=18,7;
Максимальное значение сбора овощей Х=101,3;
|
|
|
Минимальное значение величины уровня убыточности Y=8,8;
Максимальное значение величины уровня убыточности Y=78,8;
3. 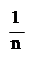 Среднее значение:
Среднее значение:
X = ∑xi.
Среднее значение величины сбора овощей X = 778,9/15 = 51,926.
Среднее значение величины уровня убыточности Y = 563,5/15 = 37,566.
4. Дисперсия
 | |||
 | |||
D(X) = ∑ (Xi – X)2 = 588.35 D(Y) = ∑(Yi – Y)2 = 385,57.
5. Среднеквадратическое отклонение:

 σx=√588.35 = 24.25, значит среднее сбора овощей в среднем от среднего значения составляет 24,25%.
σx=√588.35 = 24.25, значит среднее сбора овощей в среднем от среднего значения составляет 24,25%.
σy=√385.17 = 19.63, значит среднее уровня убыточности всей сельскохозяйственной продукции в среднем от среднего значения составляет 19,63%.
Для начала нужно определить, связаны ли X1 и Y между собой, и, если да, то определить формулу связи. По таблице строим корреляционное поле (диаграмму рассеивания). Точка с координатами (X, Y) = (51,926; 37,566) называется центром рассеяния. По виде корреляционного поля можно предположить, что зависимость между X1 и Y линейная (стр.). Для определения тесноты линейной связи найдем коэффициент корреляции:
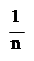 |
∑(Xi – X) (Yi – Y)
|
 rxy = = 403.64 / 24.25 х 19,63 = 0,856;
rxy = = 403.64 / 24.25 х 19,63 = 0,856;
Так как 0,6 ≤ rxy <0,9 то линейная связь между X1 и Y – достаточная. Попытаемся описать связь между X1 и Y зависимостью Y=b0+b1X. Параметры b0, b1 найдем по МНК.
b1 = rxy σx σy = -0,856 х 19,63. 24,25 = -0,696;
b0 = y – b1X = 37.566 + 0.696 х 51.92 = 73.70
Так как b1 < 0, то зависимость между X1 и Y обратная: с ростом сбора овощей уровень убыточности сельскохозяйственной продукции падает. Проверим значимость коэффициентов b0, b1.
Значимость коэффициентов b может быть проверена с помощью критерия Стьюдента:
tнабл = b0/σb0 = 73.70/6.53 = 11.28;
Значимость tнабл равна 0,00000007, т.е. 0,000007%. Так как это значение меньше 5%, то коэффициент b0 статистически значим.
tнабл = b1/σb1 = -0,696/0,1146 = -6,0716;
Значимость tнабл равна 0,000039, т.е. 0,0039%. Так как это значение меньше 5%, то коэффициент b1 статистически значим.
Получили модель связи сбора овощей и уровня убыточности сельскохозяйственной продукции:
Y = 73.70 – 0.6960X
После того, как была построена модель, необходимо проверить ее на адекватность.
|
|
|
Разброс данных, объясняемый регрессией SSR = ∑(ỹ-y)2 = 3990,5;
Остатки, необъясненный разброс SSЕ = ∑(ỹ-yi)2 = 1407,25;
Общий разброс данных SSY = ∑(yi-y)2 = 5397,85;
Для анализа общего качества оценной линейной регрессии найдем коэффициент детерминации: R2 = SSR/SSY = 0.7192;
Разброс данных объясняется линейной моделью на 72% и на 28% – случайными ошибками.
Вывод: Качество модели хорошее
Проверим с помощью критерия Фишера. Для проверки этой гипотезы сравниваются между собой величины:
MSR = SSR / K1 = 3990.5946/ K1 = 3990.5946. Отсюда K1 = 1.
MSE = SSE / K2 = 1407.25 / K2 = 108.25. Отсюда K2 = 13.
Находим наблюдаемое значение критерия Фишера Fнабл= MSR/MSE.
Значимость этого значения α = 0,00004, т.е. процент ошибки равен 0,004%. Так как это значение меньше 5%, то найденная модель считается адекватной.
Найдем прогноз на основании линейной регрессии. Выберем произвольную точку из области прогноза [18.7; 101.3]. Допустим это точка X1 = 50.
Рассчитываем прогнозные значения по модели для всех точек выборки и для точки прогноза Y(х = 50) = 73.7085 – 0.6960 х 50 = 38.9.
Найдем полуширину доверительного интервала в каждой точке выборки Xпр
Отсюда получим, что δ = 23,22.
В приведенной формуле:


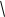

 σе = MSE = 108.25 = 10.40 – среднеквадратичное отклонение выборочных точек от линии регрессии.
σе = MSE = 108.25 = 10.40 – среднеквадратичное отклонение выборочных точек от линии регрессии.
ty = 2,16 – критическая точка распределения Стъюдента для надежности γ = 0,95 и K2 = 13 при n = 15.
SX = ∑(xi-x)2 или
SX = (n – 1) х D(X) = 14 х 588 х 39 = 8237,46;
Прогнозируемый доверительный интервал для любого X1 такой (ỹ – δ; ỹ + δ).
Совокупность доверительных интервалов для всех X1 из области прогнозов образует доверительную область, которая представляет область заключения между двумя гиперболами. Наиболее узкое место в точке X.
Прогноз для Х1 составит от 15,7 до 62,1 с гарантией 95%. То есть можно сказать, что при сборе овощей 50 центнеров с 1 га уровень убыточности сельскохозяйственной продукции можно спрогнозировать на уровне 15,7% – 62,1%.
Найдем эластичность Y = 73.70 – 0.6960X.
В нашем случае (для линейной модели) Ex = -0.6960X/(73.70 – 0.6960X).
В численном выражении это составит:
Eх=50 = -0,6960×50 / (73.70 – 0.6960×50) = – 0,8946;
Коэффициент эластичности показывает, что при изменении величины Х1 на 1% показатель Y уменьшается на 0,8946%.
Например, если Х1 = 50,5 (т.е. увеличился на 1%), то Y = 38.9 + 38.9×(-0,008946) = 38,5520006.
Проверим и Yх =50,5 = 73.70 – 0.6960X = 73.70 – 0.6960 × 50,50 = 38,552.
Задание №2
Построим нелинейную зависимость показателя от второго фактора.
Обозначим: затраты труда, человеко-часов на 1 ц – X2, а уровень убыточности как Y.
| Затраты труда, человеко-часов на 1 ц | Уровень убыточности |
| X2 | Y |
| 2,3 | 8,8 |
| 26,8 | 39,4 |
| 22,8 | 26,2 |
| 56,6 | 78,8 |
| 16,4 | 34 |
| 26,5 | 47,6 |
| 26 | 43,7 |
| 12,4 | 23,6 |
| 10 | 19,9 |
| 41,7 | 50 |
| 47,9 | 63,1 |
| 32,4 | 44,2 |
| 20,2 | 11,2 |
| 39,6 | 52,8 |
| 18,4 | 20,2 |
|
|
|
Найдем основные числовые характеристики.
6. Объем выборки n = 15 – суммарное число наблюдений.
7. Минимальное значение величины трудоемкости Х2=2,3;
Максимальное значение трудоемкости Х2=56,6;
Минимальное значение величины уровня убыточности Y=8,8;
Максимальное значение величины уровня убыточности Y=78,8;
8. 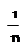 Среднее значение:
Среднее значение:
X = ∑xi.
Среднее значение величины трудоемкости X2 = 321,8/15 = 26,816.
Среднее значение величины уровня убыточности Y = 563,5/15 = 37,566.
9.  Дисперсия
Дисперсия
 |
D(X) = ∑ (Xi – X)2 = 254,66 D(Y) = ∑(Yi – Y)2 = 385,56
10. Среднеквадратическое отклонение:

 σx=√254,66 = 15,95 значит среднее трудоемкости в среднем от среднего значения составляет 15,95%.
σx=√254,66 = 15,95 значит среднее трудоемкости в среднем от среднего значения составляет 15,95%.
σy=√385.17 = 19.63, значит среднее уровня убыточности всей сельскохозяйственной продукции в среднем от среднего значения составляет 19,63%.
Для начала нужно определить, связаны ли X1 и Y между собой, и, если да, то определить формулу связи. По таблице строим корреляционное поле (диаграмму рассеивания). Точка с координатами (X, Y) = (26,816; 37,566) называется центром рассеяния. По виде корреляционного поля можно предположить, что зависимость между X1 и Y нелинейная (стр.), а именно имеет зависимость 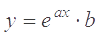 .
.
Путем преобразования нелинейную зависимость приведем к линейной V = b0 + b1U.
Для начала заменим переменные U = x, а V = ln(Y).
Найдем конкретные значения V и U (стр.), затем строим корреляционное поле (стр.) и находим результаты регрессивной статистики.
Для определения тесноты линейной связи V = b0 + b1U найдем коэффициент корреляции:
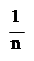 |
∑(Ui – U) (Vi – V)
|
 rvu = = 403.64 / 24.25 х 19,63 = 0,856;
rvu = = 403.64 / 24.25 х 19,63 = 0,856;
Так как 0,6 ≤ rxy <0,9 то линейная связь между X1 и Y – достаточная. Попытаемся описать связь между X1 и Y зависимостью Y=b0+b1X. Параметры b0, b1 найдем по МНК.
b1 = rvu σv σu = -0,856 х 19,63. 24,25 = -0,696;
b0 = y – b1X = 37.566 + 0.696 х 51.92 = 73.70
Так как b1 < 0, то зависимость между X1 и Y обратная: с ростом сбора овощей уровень убыточности сельскохозяйственной продукции падает. Проверим значимость коэффициентов b0, b1.
Значимость коэффициентов b может быть проверена с помощью критерия Стьюдента:
tнабл = b0/σb0 = 73.70/6.53 = 11.28;
Значимость tнабл равна 0,00000007, т.е. 0,000007%. Так как это значение меньше 5%, то коэффициент b0 статистически значим.
tнабл = b1/σb1 = -0,696/0,1146 = -6,0716;
Значимость tнабл равна 0,000039, т.е. 0,0039%. Так как это значение меньше 5%, то коэффициент b1 статистически значим.
Получили модель связи сбора овощей и уровня убыточности сельскохозяйственной продукции:
Y = 73.70 – 0.6960 X
После того, как была построена модель, необходимо проверить ее на адекватность.
Разброс данных, объясняемый регрессией SSR = ∑(ỹ-y)2 = 3990,5;
Остатки, необъясненный разброс SSЕ = ∑(ỹ-yi)2 = 1407,25;
Общий разброс данных SSY = ∑(yi-y)2 = 5397,85;
Для анализа общего качества оценной линейной регрессии найдем коэффициент детерминации: R2 = SSR/SSY = 0.7192;
Разброс данных объясняется линейной моделью на 72% и на 28% – случайными ошибками.
Вывод: Качество модели хорошее
Проверим с помощью критерия Фишера. Для проверки этой гипотезы сравниваются между собой величины:
MSR = SSR / K1 = 3990.5946/ K1 = 3990.5946. Отсюда K1 = 1.
MSE = SSE / K2 = 1407.25 / K2 = 108.25. Отсюда K2 = 13.
Находим наблюдаемое значение критерия Фишера Fнабл= MSR/MSE.
Значимость этого значения α = 0,00004, т.е. процент ошибки равен 0,004%. Так как это значение меньше 5%, то найденная модель считается адекватной.
Найдем прогноз на основании линейной регрессии. Выберем произвольную точку из области прогноза [18.7; 101.3]. Допустим это точка X1 = 50.
Рассчитываем прогнозные значения по модели для всех точек выборки и для точки прогноза Y(х = 50) = 73.7085 – 0.6960 х 50 = 38.9.
Найдем полуширину доверительного интервала в каждой точке выборки Xпр
Отсюда получим, что δ = 23,20.
В приведенной формуле:


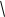

 σе = MSE = 108.25 = 10.40 – среднеквадратичное отклонение выборочных точек от линии регрессии.
σе = MSE = 108.25 = 10.40 – среднеквадратичное отклонение выборочных точек от линии регрессии.
ty = 2,16 – критическая точка распределения Стъюдента для надежности γ = 0,95 и K2 = 13 при n = 15.
SX = ∑(xi-x)2 или
SX = (n – 1) х D(X) = 14 х 588 х 39 = 8237,46;
Прогнозируемый доверительный интервал для любого X1 такой (ỹ – δ; ỹ + δ).
Совокупность доверительных интервалов для всех X1 из области прогнозов образует доверительную область, которая представляет область заключения между двумя гиперболами. Наиболее узкое место в точке X.
Прогноз для Х1 составит от 15,7 до 62,1 с гарантией 95%. То есть можно сказать, что при сборе овощей 50 центнеров с 1 га уровень убыточности сельскохозяйственной продукции можно спрогнозировать на уровне 15,7% – 62,1%.
Найдем эластичность Y = 73.70 – 0.6960X.
В нашем случае (для линейной модели) Ex = -0.6960X/(73.70 – 0.6960X).
В численном выражении это составит:
Eх=50 = -0,6960×50 / (73.70 – 0.6960×50) = – 0,8946;
Коэффициент эластичности показывает, что при изменении величины Х1 на 1% показатель Y уменьшается на 0,8946%.
Например, если Х1 = 50,5 (т.е. увеличился на 1%), то Y = 38.9 + 38.9×(-0,008946) = 38,5520006.
Проверим и Yх =50,5 = 73.70 – 0.6960X = 73.70 – 0.6960 × 50,50 = 38,552.
Задание №3
| Сбор овощей с 1 га, ц | Затраты труда, человеко-часов на 1 ц | Уровень убыточности |
| X 1 | X 2 | Y |
| 93,2 | 2,3 | 8,8 |
| 65,9 | 26,8 | 39,4 |
| 44,6 | 22,8 | 26,2 |
| 18,7 | 56,6 | 78,8 |
| 64,6 | 16,4 | 34 |
| 25,6 | 26,5 | 47,6 |
| 47,2 | 26 | 43,7 |
| 48,2 | 12,4 | 23,6 |
| 64,1 | 10 | 19,9 |
| 30,3 | 41,7 | 50 |
| 28,4 | 47,9 | 63,1 |
| 47,8 | 32,4 | 44,2 |
| 101,3 | 20,2 | 11,2 |
| 31,4 | 39,6 | 52,8 |
| 67,6 | 18,4 | 20,2 |
Построим линейную зависимость показателя от двух факторов.
Обозначим: сбор овощей с 1 га как X1, затраты труда, человеко-часов на 1 ц – X2, а уровень убыточности как Y.
Найдем основные числовые характеристики.
1. Объем выборки n = 15 – суммарное число наблюдений
2. Минимальное значение величины сбора овощей Х1=18,7;
Максимальное значение сбора овощей Х1=101,3;
Минимальное значение величины трудоемкости Х2=2,3;
Максимальное значение трудоемкости Х2=56,6;
Минимальное значение величины уровня убыточности Y=8,8;
Максимальное значение величины уровня убыточности Y=78,8;
3. Среднее значение:
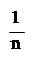 |
X = ∑xi.
Среднее значение величины сбора овощей X = 778,9/15 = 51,926.
Среднее значение величины трудоемкости X2 = 321,8/15 = 26,816.
Среднее значение величины уровня убыточности Y = 563,5/15 = 37,566.
4. Дисперсия
 | |||
 | |||
D(X) = ∑ (Xi – X)2 = 254,66 D(Y) = ∑(Yi – Y)2 = 385,56
5. Среднеквадратическое отклонение:

 σx=√254,66 = 15,95 значит среднее трудоемкости в среднем от среднего значения составляет 15,95%.
σx=√254,66 = 15,95 значит среднее трудоемкости в среднем от среднего значения составляет 15,95%.
σy=√385.17 = 19.63, значит среднее уровня убыточности всей сельскохозяйственной продукции в среднем от среднего значения составляет 19,63%.
Для начала нужно определить, связаны ли X1 и Y между собой, и, если да, то определить формулу связи. По таблице строим корреляционное поле (диаграмму рассеивания). Точка с координатами (X, Y) = (26,816; 37,566) называется центром рассеяния. По виде корреляционного поля можно предположить, что зависимость между X1 и Y нелинейная (стр.), а именно имеет зависимость 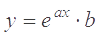 .
.
Путем преобразования нелинейную зависимость приведем к линейной V = b0 + b1U.
Для начала заменим переменные U = x, а V = ln(Y).
Найдем конкретные значения V и U (стр.), затем строим корреляционное поле (стр.) и находим результаты регрессивной статистики.
Для определения тесноты линейной связи V = b0 + b1U найдем коэффициент корреляции:
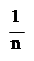 |
∑(Ui – U) (Vi – V)
|
 rvu = = 403.64 / 24.25 х 19,63 = 0,856;
rvu = = 403.64 / 24.25 х 19,63 = 0,856;
Так как 0,6 ≤ rxy <0,9 то линейная связь между X1 и Y – достаточная. Попытаемся описать связь между X1 и Y зависимостью Y=b0+b1X. Параметры b0, b1 найдем по МНК.
и1 = кчн σн. σч = -0,856 х 19,63. 24,25 = -0,696;
b0 = y – b1X = 37.566 + 0.696 х 51.92 = 73.70
Так как b1 < 0, то зависимость между X1 и Y обратная: с ростом сбора овощей уровень убыточности сельскохозяйственной продукции падает. Проверим значимость коэффициентов b0, b1.
Значимость коэффициентов b может быть проверена с помощью критерия Стьюдента:
tнабл = b0/σb0 = 73.70/6.53 = 11.28;
tнабл = b1/σb1 = -0,696/0,1146 = -6,0716;
Значимость tнабл равна 0,000039, т.е. 0,0039%. Так как это значение меньше 5%, то коэффициент b1 статистически значим.
Получили модель связи сбора овощей и уровня убыточности сельскохозяйственной продукции:
Y = 73.70 – 0.6960 X
После того, как была построена модель, необходимо проверить ее на адекватность.
Разброс данных, объясняемый регрессией SSR = ∑(ỹ-y)2 = 3990,5;
Остатки, необъясненный разброс SSЕ = ∑(ỹ-yi)2 = 1407,25;
Общий разброс данных SSY = ∑(yi-y)2 = 5397,85;
Для анализа общего качества оценной линейной регрессии найдем коэффициент детерминации: R2 = SSR/SSY = 0.7192;
Разброс данных объясняется линейной моделью на 72% и на 28% – случайными ошибками.
Вывод: Качество модели хорошее
Проверим с помощью критерия Фишера. Для проверки этой гипотезы сравниваются между собой величины:
MSR = SSR / K1 = 3990.5946/ K1 = 3990.5946. Отсюда K1 = 1.
MSE = SSE / K2 = 1407.25 / K2 = 108.25. Отсюда K2 = 13.
Находим наблюдаемое значение критерия Фишера Fнабл= MSR/MSE.
Значимость этого значения α = 0,00004, т.е. процент ошибки равен 0,004%. Так как это значение меньше 5%, то найденная модель считается адекватной.
Найдем прогноз на основании линейной регрессии. Выберем произвольную точку из области прогноза [18.7; 101.3]. Допустим это точка X1 = 50.
Рассчитываем прогнозные значения по модели для всех точек выборки и для точки прогноза Y(х = 50) = 73.7085 – 0.6960 х 50 = 38.9.
Найдем полуширину доверительного интервала в каждой точке выборки Xпр
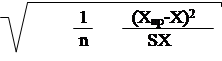 | |||
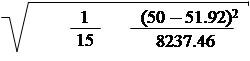 | |||
δ = σе ty 1 + + = 10.4 × 2.016 1 + +
Отсюда получим, что δ = 23,20.
В приведенной формуле:


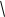

 σе = MSE = 108.25 = 10.40 – среднеквадратичное отклонение выборочных точек от линии регрессии.
σе = MSE = 108.25 = 10.40 – среднеквадратичное отклонение выборочных точек от линии регрессии.
ty = 2,16 – критическая точка распределения Стъюдента для надежности γ = 0,95 и K2 = 13 при n = 15.
SX = ∑(xi-x)2 или
SX = (n – 1) х D(X) = 14 х 588 х 39 = 8237,46;
Прогнозируемый доверительный интервал для любого X1 такой (ỹ – δ; ỹ + δ).
Совокупность доверительных интервалов для всех X1 из области прогнозов образует доверительную область, которая представляет область заключения между двумя гиперболами. Наиболее узкое место в точке X.
Прогноз для Х1 составит от 15,7 до 62,1 с гарантией 95%. То есть можно сказать, что при сборе овощей 50 центнеров с 1 га уровень убыточности сельскохозяйственной продукции можно спрогнозировать на уровне 15,7% – 62,1%.
Найдем эластичность Y = 73.70 – 0.6960X.
В нашем случае (для линейной модели) Ex = -0.6960X/(73.70 – 0.6960X).
В численном выражении это составит:
Eх=50 = -0,6960×50 / (73.70 – 0.6960×50) = – 0,8946;
Коэффициент эластичности показывает, что при изменении величины Х1 на 1% показатель Y уменьшается на 0,8946%.
Например, если Х1 = 50,5 (т.е. увеличился на 1%), то Y = 38.9 + 38.9×(-0,008946) = 38,5520006.
Проверим и Yх =50,5 = 73.70 – 0.6960X = 73.70 – 0.6960 × 50,50 = 38,552.
|
|
|


