 |
Преобразование Галилея. (Одно занятие)
|
|
|
|
Задача 31
Одна из звезд нашей вселенной покоится, а все остальные звезды разлетаются от нее в разные стороны со скоростями, пропорциональными расстояниям от них до покоящейся звезды. Какую картину движения обнаружит наблюдатель, движущийся вместе с другой звездой нашей вселенной?
Ответ: не скажу
Задача 32
Какой будет продолжительность полета из Новосибирска в Москву и обратно, если полет проходит по прямой, а в течение всего времени полета дует ветер со скоростью u под углом α к трассе? Скорость самолета относительно воздуха v, длина трассы L. При каком направлении ветра продолжительность полета максимальна?
Ответ: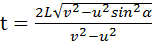 
, когда ветер дует вдоль трассы
Задача 33
Тело налетает на стенку со скоростью v под углом α к линии, перпендикулярной стенке. Определите скорость тела после упругого удара, если стенка: а) неподвижна; б) движется перпендикулярно самой себе со скоростью w навстречу телу; в) движется под углом β к линии, перпендикулярной ей самой, со скоростью w навстречу телу.
Ответ: а) 
; б) 
; в) 
Задача 34
Тело влетает горизонтально со скоростью v в пространство между двумя вертикальными стенками, которые перемещаются со скоростью u. Определите скорость тела после n -го удара о переднюю стенку. Расстояние между стенками L. Удары абсолютно упругие. Ускорение свободного падения g.
Ответ: проекции скорости будут равны 
; 
Задача 35
Между двумя стенками со скоростью v летает шарик. Одна из стенок начинает с бесконечно-малой скоростью приближаться к другой. Начальное расстояние между стенками L. Какой будет скорость шарика, когда расстояние между стенками будет L/2? Столкновения шарика со стенками упругие.
Ответ: 
Задача 36
|
|
|
Два пучка частиц, движущихся с одинаковой по модулю скоростью v, пересекаются под углом α. Соударения частиц происходят в ограниченной области. Перейдем к системе отсчета, в которой скорости частиц равны по модулю и противоположны по направлению. Казалось бы, теперь область пересечения – весь объем пучков, и поэтому число соударений в единицу времени должно быть больше. Объясните получившееся противоречие.
Ответ: кто списал тот молодец, посмотрим, кто сможет объяснить.
Задача 37
Мальчик, который может плавать со скоростью, в два раза меньшей скорости течения реки, хочет переплыть эту реку так, чтобы его как можно меньше снесло вниз по течению. Под каким углом к берегу он должен плыть? На какое расстояние его снесет, если ширина реки равна 200 м?
Ответ: 
Движение со связями.
Задача 38
Угловая скорость катушки равна ω, радиус внутреннего цилиндра r, а радиус внешних цилиндров R. Каковы скорости оси катушки и груза относительно земли?
Ответ: 
Задача 39
На клине с углом α лежит монета. С каким наименьшим ускорением должен двигаться клин по горизонтальной плоскости, чтобы монета свободно падала вниз?
Ответ: 
Задача 40
Скорости точек A и B твердого тела равны v. Скорость точки С, находящейся в плоскости прямой AB и вектора v, равна u > v. Найдите проекцию скорости точки С на ось, перпендикулярную указанной плоскости.
Ответ: 
Задача 41
Постройте траектории точек колеса, катящегося без проскальзывания по рельсу. Рассмотрите случаи когда точки находятся от оси колеса на расстоянии: r > R, r = R, r < R. Найдите ускорение этих точек, если ось колеса движется с постоянной скоростью v.
Ответ: 
Задача 42
Луна обращена к Земле постоянно одной стороной. Сколько оборотов совершит она вокруг своей оси за время полного оборота вокруг Земли?
Ответ: простой
Задача 43
Веревку, привязанную к лодке, тянут за свободный конец таким образом, чтобы она не провисала. Лодка движется с постоянной скоростью v, образуя в некоторый момент времени угол α с отрезком веревки, находящимся между столбом и лодкой. С какой скоростью нужно тянуть в этот момент времени свободный конец веревки?
|
|
|
Ответ: 
Задача 44
Стержень длины L упирается своими концами в стороны прямого угла. Верхний конец стержня поднимают со скоростью v. Найдите, как зависит от времени скорость его нижнего конца. Начало отсчета времени считать моментом, когда верхний конец стержня находится в вершине прямого угла.
Ответ: 
Задача 45
Бревно, упираясь нижним своим концом в угол между стеной и землей, касается дна грузовика на высоте H от земли. Найдите угловую скорость бревна в зависимости от угла α между ним и горизонтом, если грузовик отъезжает от стены со скоростью v.
Ответ: 
Динамика.
Законы Ньютона.
Задача 1
Шайба, скользившая по льду, остановилась через время t = 5 с после удара о клюшку на расстоянии l = 20 м от места удара. Масса шайбы m = 100 г. Определите действовавшую на шайбу силу трения.
Ответ: 16Н
Задача 2
Два тела массы 
и 
связаны нитью, выдерживающей силу натяжения T. К телам приложены силы 
и 
, где α – постоянный коэффициент, а t – время действия силы. Определите, в какой момент времени нить порвется.
Ответ: 
Задача 3
Для подготовки к работе в условиях невесомости одетые в скафандры космонавты тренируются в воде. При этом сила тяжести, действующая на них, уравновешивается выталкивающей силой. В чем отличие такой «невесомости» от настоящей?
Ответ: тут думать надо
Задача 4
Маляр работает в подвесной люльке. Ему понадобилось срочно подняться вверх. Он насинает тянуть за веревку с такой силой, что сила его давления на пол люльки уменьшилась до 400 Н. Масса люльки 12 кг. Масса маляра 72 кг. Чему равно ускорение люльки?
Ответ: 
Задача 5
Тела массы и соединены пружиной жесткости k. На тело массы действует постоянная сила F, направленная вдоль пружины к телу массы . Найдите на сколько сжата пружина, если никаких других внешних сил нет, а колебания уже прекратились. Каким будет ускорение тел сразу же после прекращения действия силы F?
Ответ: 
Задача 6
Если нажимать пальцем на шариковую ручку, опирающуюся на твердую поверхность, одновременно наклоняя ее, то, пока ручка образует малый угол с перпендикуляром к поверхности, она будет следовать за пальцем (как шарнирно закрепленная). Как только угол наклона достигнет какого-то значения 
, она выскользнет из-под пальца, независимо от приложенной силы. Поэкспериментируйте и оцените коэффициент трения между шариком ручки и поверхностью, на которую она опирается.
|
|
|
Ответ: это ваш эксперимент, у каждого будет свой ответ
Задача 7
На горизонтальной доске лежит брусок массы m. Доску медленно наклоняют. Определите зависимость силы трения действующей на брусок, от угла наклона доски α. Коэффициент трения μ.
Ответ: 
Задача 8
Через какое время скорость тела, которому сообщили вверх по наклонной плоскости скорость v, снова будет равна v? Коэффициент трения μ, угол между плоскостью и горизонтом α.
Ответ: 
Задача 9
На тело массы m, лежащее на горизонтальной плоскости, действует сила F под углом α к горизонту. Коэффициент трения μ. Найдите ускорение тела, если оно не отрывается от плоскости.
Ответ: 
Задача 10
Нить, перекинутая через блок с неподвижной осью, пропущена через щель. На концах нити подвешены грузы, масса которых и . Определите ускорения грузов, если при движении нити на нее со стороны щели действует постоянная сила трения 
.
Ответ: 
Задача 11
Коэффициент трения шипованных шин на обледеневшей дороге в десять раз больше чем нешипованных. Во сколько раз нужно занижать скорость движения, чтобы длина тормозного пути оставалась прежней?
Ответ: готовьтесь к взрослой жизни, будущие водители=)
Задача 12
Спортивный автомобиль, трогаясь с места разгоняется до 72 км/ч за 5 с (быстрее невозможно в силу проскальзывания колес). Каков коэффициент трения между колесами и дорогой? Каким будет наименьший тормозной путь данного автомобиля при торможении с той же скорости?
Ответ: а вдруг вы купите спорткар?
Задача 13
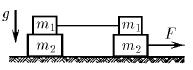На гладком горизонтальном столе расположена система грузов, изображенная на рисунке. Правый нижний груз тянут вдоль стола с силой F, как указано на рисунке. Коэффициент трения между грузами массы и равен μ. Найдите ускорение всех грузов системы.
|
|
|
Ответ: 
Задача 14
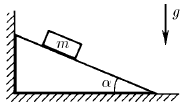Определите силу действующую на вертикальную стенку со стороны клина, если на него положили груз массы m. Угол при основании клина α. Коэффициент трения между грузом и клином μ. Трения между клином и полом нет.
Ответ: 
Задача 15
Сила сопротивления воздуха действующая на велосипедиста пропорциональна квадрату скорости велосипедиста 
. На горизонтальной дороге наибольшая скорость велосипедиста составляет примерно 20 м/с. Оцените коэффициент пропорциональности α, если масса велосипедиста вместе с велосипедом 70 кг, а коэффициент трения между колесами и дорогой 0,4.
Ответ: 
Задача 1.дз
Сила сопротивления воздуха, действующая на капли дождя, пропорциональна произведению квадрата скорости капель на квадрат их радиуса: 
, где ρ – плотность воздуха, а безразмерный коэффициент 
равен приблизительно 0,16 (таким образом, коэффициент 
). Какие капли, крупные или мелкие, падают на землю с большей скоростью? Оцените скорость капли радиусом в 1 мм при падении с большой высоты.
Задача 2.дз
Сила сопротивления воздуха, действующая на капли тумана, пропорциональна произведению радиуса на скорость: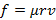 
. Капли радиуса 0,1 мм падая с большой высоты имеют скорость порядка 1 м/с. Какую скорость будут иметь капли, радиус которых в два раза меньше? А в десять раз?
Задача 3.дз
Сила сопротивления жидкости или газа, пропорциональная квадрату скорости движущегося теля, связана с образованием вихрей вблизи поверхности этого тела. Сила сопротивления, пропорциональная скорости движущегося тела, связана с проскальзыванием слоев среды при обтекании ею этого теля. Оба явления всегда проходят одновременно. Почему тем не менее в тех или иных случаях можно принимать во внимание только один какой-либо вид сопротивления? По данным двух предыдущих задач оцените, при каком значении произведения радиуса круглой капли на ее скорость оба вида сопротивления воздуха сравнимы по своему воздействию на движение капли.
Задача 16
Почему крепко засевший в бревне гвоздь проще вытащить, если при этом его вращать вокруг своей оси?
Ответ: потому
Задача 17
По наклонной плоскости скользят два тела одинаковой массы, связанные нитью. Сила натяжения нити T. Трения между одним телом и плоскостью нет. Определите силу трения между доской и другим телом.
Ответ: очевиден
Задача 18
Между двумя гладкими брусками массы каждый вставлен клин массы и с углом раствора α. Определите ускорение всех тел системы. Трения нет
|
|
|
Ответ: 
; 
;
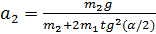Задача 19
На гладкой горизонтальной плоскости находится клин с углом раствора α. Тело массы m, положенное на клин, опускается с ускорением, направленным под углом β > α к горизонту. Определите массу клина.
Ответ: 
Задача 20
Ускорение звезд, входящих в состав двойной звезды, 
и 
. Какова масса второй звезды, если масса первой ?
Ответ: слишком просто
Задача 21
В сферическую полость положили гантель с шариками массы m и невесомым стержнем так, как это показано на рисунке. Определите силу давления шариков на стенки сразу после того, как гантель отпустили. Радиус шариков много меньше радиуса сферы.
Ответ: для верхнего mg/2, для нижнего 3mg/2
Задача 4.дз
Электроны, движущиеся по окружности любого радиуса вокруг заряженной нити, имеют одну и ту же скорость v. Масса электрона me. Как зависит сила, действующая со стороны нити на электрон, от расстояния между электроном и нитью? Опишите качественно начальный отрезок траектории, по которой будет двигаться электрон, если скорость его движении по окружности станет вдруг чуть меньше v? Чуть больше v?
Задача 22
Два шарика массы m каждый связаны нитью длины l и движутся со скоростью v по горизонтальному столу в направлении, перпендикулярном связывающей их нити. Нить не провисает. Середина нити налетает на гвоздь вбитый в поверхность стола. Чему равна сила натяжения нити в этот момент?
Ответ: халява
Задача 23
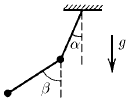
К тяжелому шарику, подвешенному на нити длины l, подвешен другой тяжелый шарик на нити той же длины. При вращении шариков вокруг вертикальной оси, проходящей через верхнюю точку подвеса первого шарика, обе нити лежат в одной плоскости и составляют с вертикалью постоянные углы α и β. Найдите угловую скорость вращения шариков.
Ответ: 
Задача 24
Груз массы m, прикрепленный пружиной жесткости k к оси, движется вокруг этой оси по окружности радиуса R с угловой скоростью ω. Какова длина недеформированной пружины?
Ответ: 
;
Задача 25
Самолет совершает вираж, двигаясь по горизонтальной окружности радиуса R с постоянной скоростью v. Какой угол составляет плоскость крыла самолета с горизонтом?
Ответ: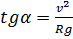 
Задача 26
Горизонтальный диск начинают раскручивать вокруг своей оси с линейно возрастающей по времени угловой скоростью 
. При какой угловой скорости тело, расположенное на расстоянии r от оси диска начнет соскальзывать с него, если коэффициент трения между ними равен μ?
Ответ: 
; 
Задача 27
С какой максимальной скоростью может ехать по горизонтальной плоскости мотоциклист, описывая круг радиуса R, если коэффициент трения равен μ? На какой угол от вертикали он должен при этом отклониться? Во сколько раз увеличится максимально допустимая скорость мотоциклиста при движении по наклонному треку с углом наклона α к горизонту по сравнению с максимально допустимой скоростью при движении по горизонтальному треку при том же радиусе поворота и том же коэффициенте трения.
Ответ: 
|
|
|
