 |
Плотность распределения непрерывной случайной величины
|
|
|
|
Непрерывные случайные величины
№1
24.1.1./1
УС 1
АБ
Время: 1 мин.
Функция распределения F(x) непрерывной случайной величины X определяет вероятность того, что случайная величина X в результате испытания примет значение…
+ меньшее x
- меньшее или равное x
- большее x
- большее или равное x
- равное x
№2
24.1.1./2
УС 1
АБ
Время: 1 мин.
Значения функции распределения F(x) непрерывной случайной величины X принадлежат промежутку…
+ [0;1]
- (0;1)
- (0;1]
- [0;1)
№3
24.1.1./3
УС 1
АБ
Время: 1 мин.
Функция распределения F(x) непрерывной случайной величины X есть функция…
+ неубывающая
- невозрастающая
- постоянная
- убывающая
- возрастающая
№4
24.1.1./4
УС 1
АБ
Время: 1 мин.
Вероятность того, что непрерывная случайная величина X с заданной функцией распределения F(x) примет значение, заключенное в интервале (a,b), равна…
+ F(b) – F(a)
- F(a) – F(b)
- F(b-a)
- F(a-b)
- F(b/a)
№5
24.1.1./5
УС 1
АБ
Время: 1 мин.
Вероятность того, что непрерывная случайная величина X с заданной функцией распределения F(x) примет одно определенное значение, например x1, равна…
+ 0
- x1
- 1
- 1 - x1
№6
24.1.1./6
УС 1
АБ
Время: 1 мин.
Предельные соотношения для функции распределения F(x) непрерывной случайной величины X:
+ 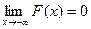
+ 
- 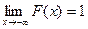
- 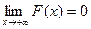
№7
24.1.1./7
УС 1
АБ
Время: 1 мин.
Случайная величина X задана функцией распределения:
F(x) = 0 при x≤ 2,
F(x) = 0,5 x -1при 2< x ≤4,
F(x) = 1 при x >4.
Вероятность того, что в результате испытания X примет значение, меньшее трех, равна…
+ 0,5
- 0
- 1
- 1,5
№8
24.1.1./8
УС 1
АБ
Время: 1 мин.
Случайная величина X задана функцией распределения:
F(x) = 0 при x≤ 2,
F(x) = 0,5 x -1при 2< x ≤4,
F(x) = 1 при x >4.
Вероятность того, что в результате испытания X примет значение, заключенное в интервале (0,5;1,5), равна…
|
|
|
+ 0
- 0,5
- 1
- 1,5
№9
24.1.1./9
УС 1
АБ
Время: 1 мин.
Случайная величина X задана функцией распределения:
F(x) = 0 при x≤ 2,
F(x) = 0,5 x -1при 2< x ≤4,
F(x) = 1 при x >4.
Вероятность того, что в результате испытания X примет значение, большее двух, равна…
+ 1
- 0
- 0,5
- 2
№10
24.1.1./8
УС 1
АБ
Время: 1 мин.
Случайная величина X задана функцией распределения:
F(x) = 0 при x≤ 2,
F(x) = 0,2 x -0,4 при 2< x ≤7,
F(x) = 1 при x >7.
Вероятность того, что в результате испытания X примет значение, меньшее пяти, равна…
+ 0,6
- 0
- 1
- 0,4
№11
24.1.1./11
УС 1
АБ
Время: 1 мин.
Случайная величина X задана функцией распределения:
F(x) = 0 при x≤ 2,
F(x) = 0,2 x -0,4 при 2< x ≤7,
F(x) = 1 при x >7.
Вероятность того, что в результате испытания X примет значение, заключенное в интервале (3;4), равна…
+ 0,2
- 0
- 1
- 0,8
№12
24.1.1./12
УС 1
АБ
Время: 1 мин.
Случайная величина X задана функцией распределения:
F(x) = 0 при x≤ 2,
F(x) = 0,2 x -0,4 при 2< x ≤7,
F(x) = 1 при x >7.
Вероятность того, что в результате испытания X примет значение, большее пяти, равна…
+ 0,4
- 0
- 1
- 0,6
№13
24.1.1./13
УС 1
АБ
Время: 1 мин.
Случайная величина X задана функцией распределения:
F(x) = 0 при x≤ 0,
F(x) = 0,25 x при 0< x ≤4,
F(x) = 1 при x >4.
Вероятность того, что в результате испытания X примет значение, меньшее трех, равна…
+ 0,75
- 0
- 1
- 0,25
№14
24.1.1./14
УС 1
АБ
Время: 1 мин.
Случайная величина X задана функцией распределения:
F(x) = 0 при x≤ 0,
F(x) = 0,25 x при 0< x ≤4,
F(x) = 1 при x >4.
Вероятность того, что в результате испытания X примет значение, заключенное в интервале (-1;4), равна…
+ 0,5
- 0
- 1
- 1,25
№15
24.1.1./15
УС 1
АБ
Время: 1 мин.
Случайная величина X задана функцией распределения:
F(x) = 0 при x≤ 0,
F(x) = 0,25 x при 0< x ≤4,
F(x) = 1 при x >4.
Вероятность того, что в результате испытания X примет значение, большее единицы, равна…
+ 0,75
- 0
- 1
- 0,25
№16
24.1.1./16
УС 1
|
|
|
АБ
Время: 1 мин.
Случайная величина X задана функцией распределения:
F(x) = 0 при x≤ 0,
F(x) = x /2 при 0< x ≤2,
F(x) = 1 при x >2.
Вероятность того, что в результате испытания X примет значение, заключенное в интервале (1;2), равна…
+ 0,5
- 0
- 1
- 1,5
№17
24.1.1./17
УС 1
АБ
Время: 1 мин.
Случайная величина X задана функцией распределения:
F(x) = 0 при x≤ 0,
F(x) = x /3 при 0< x ≤3,
F(x) = 1 при x >3.
Вероятность того, что в результате испытания X примет значение, заключенное в интервале (2;3), равна…
+ 1/3
- 0
- 1
- 2/3
№18
24.1.1./18
УС 1
АБ
Время: 1 мин.
Случайная величина X задана функцией распределения:
F(x) = 0 при x≤ 0,
F(x) = x /4 при 0< x ≤4,
F(x) = 1 при x >4.
Вероятность того, что в результате испытания X примет значение, заключенное в интервале (4;5), равна…
+ 0
- 4/5
- 1
- 1/4
Плотность распределения непрерывной случайной величины
№1
24.1.2./1
УС 1
АБ
Время: 1 мин.
Плотность распределения f(x) и функция распределения F(x) непрерывной случайной величины X связаны формулой:
+ f(x) = F'(x)
+ 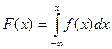
- F(x) = f '(x)
- 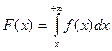
- f(x) = F(x) + C
№2
24.1.2./2
УС 1
АБ
Время: 1 мин.
Плотность распределения f(x) непрерывной случайной величины X есть функция…
+ неотрицательная
- неположительная
- знакопеременная
- отрицательная
- положительная
№3
24.1.2./3
УС 1
АБ
Время: 1 мин.
Несобственный интеграл  от плотности распределения f(x) непрерывной случайной величины равен…
от плотности распределения f(x) непрерывной случайной величины равен…
+ единице
- нулю
- функции распределения F(x)
- не существует
№4
24.1.2./4
УС 1
АБ
Время: 1 мин.
Вероятность P того, что непрерывная случайная величина X с плотностью распределения f(x) примет значение, принадлежащее интервалу (a,b), определяется равенством…
+ 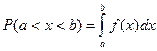
- 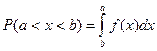
- 
- 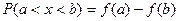
- 
№5
24.1.2./5
УС 1
АБ
Время: 1 мин.
Значение функции распределения F(π /3 ) при заданной плотности распределения f(x) непрерывной случайной величины X
f(x) = 0 при x≤ 0,
f(x) = sinx при 0< x≤ π/2,
f(x) = 0 при x> π/2,
равно…
+ 1/2
- 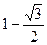
- 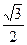
- 0
№6
24.1.2./6
УС 1
АБ
Время: 1 мин.
Значение функции распределения F(π /6 ) при заданной плотности распределения f(x) непрерывной случайной величины X
f(x) = 0 при x≤ 0,
f(x) = sinx при 0< x≤ π/2,
f(x) = 0 при x> π/2,
равно…
+ 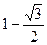
- 1/2
- 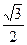
- 0
№7
24.1.2./7
УС 1
АБ
Время: 1 мин.
Значение функции распределения F(π) при заданной плотности распределения f(x) непрерывной случайной величины X
|
|
|
f(x) = 0 при x≤ 0,
f(x) = sinx при 0< x≤ π/2,
f(x) = 0 при x> π/2,
равно…
+ 1
- 1/2
- 2
- 0
№8
24.1.2./8
УС 1
АБ
Время: 1 мин.
Значение функции распределения F( 3/4 ) при заданной плотности распределения f(x) непрерывной случайной величины X
f(x) = 0 при x≤ 1,
f(x) = x – 1/2при 1< x≤ 2,
f(x) = 0 при x> 2,
равно…
+ 0
- 1/4
- 3/32
- 1
№9
24.1.2./9
УС 1
АБ
Время: 1 мин.
Значение функции распределения F( 3 ) при заданной плотности распределения f(x) непрерывной случайной величины X
f(x) = 0 при x≤ 1,
f(x) = x – 1/2при 1< x≤ 2,
f(x) = 0 при x> 2,
равно…
+ 1
- 5/2
- 2/5
- 0
№10
24.1.2./10
УС 1
АБ
Время: 1 мин.
Значение функции распределения F( 3/2 ) при заданной плотности распределения f(x) непрерывной случайной величины X
f(x) = 0 при x≤ 1,
f(x) = x – 1/2при 1< x≤ 2,
f(x) = 0 при x> 2,
равно…
+ 3/8
- 3/4
- 0
- 1
№11
24.1.2./11
УС 1
АБ
Время: 1 мин.
Значение плотности распределения f(π /6 ) при заданной функции распределения F(x) непрерывной случайной величины X
F(x) = 0 при x≤ 0,
F(x) = sinx при 0< x≤ π/2,
F(x) = 1 при x> π/2,
равно…
+ 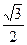
- 1/2
- 1
- 0
№12
24.1.2./12
УС 1
АБ
Время: 1 мин.
Значение плотности распределения f(π /3 ) при заданной функции распределения F(x) непрерывной случайной величины X
F(x) = 0 при x≤ 0,
F(x) = sinx при 0< x≤ π/2,
F(x) = 1 при x> π/2,
равно…
+ 1/2
- 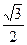
- 1
- 0
№13
24.1.2./13
УС 1
АБ
Время: 1 мин.
Значение плотности распределения f(π) при заданной функции распределения F(x) непрерывной случайной величины X
F(x) = 0 при x≤ 0,
F(x) = sinx при 0< x≤ π/2,
F(x) = 1 при x> π/2,
равно…
+ 0
- 1/2
- 1
- -1
№14
24.1.2./14
УС 1
АБ
Время: 1 мин.
Значение плотности распределения f(-π /4 ) при заданной функции распределения F(x) непрерывной случайной величины X
F(x) = 0 при x≤ 0,
F(x) = sinx при 0< x≤ π/2,
F(x) = 1 при x> π/2,
равно…
+ 0
- 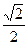
- 1
- 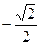
№15
24.1.2./15
УС 1
АБ
Время: 1 мин.
Значение плотности распределения f(- 1/4 ) при заданной функции распределения F(x) непрерывной случайной величины X
F(x) = 0 при x≤ 0,
F(x) = x2 при 0< x≤ 1,
F(x) = 1 при x> 1,
равно…
+ 0
- 1/16
- -1/16
- -1/2
- 1
№16
24.1.2./16
|
|
|
УС 1
АБ
Время: 1 мин.
Значение плотности распределения f( 1/4 ) при заданной функции распределения F(x) непрерывной случайной величины X
F(x) = 0 при x≤ 0,
F(x) = x2 при 0< x≤ 1,
F(x) = 1 при x> 1,
равно…
+ 1/2
- 0
- 1
- 1/16
- 1/192
№17
24.1.2./17
УС 1
АБ
Время: 1 мин.
Значение плотности распределения f( 4/3 ) при заданной функции распределения F(x) непрерывной случайной величины X
F(x) = 0 при x≤ 0,
F(x) = x2 при 0< x≤ 1,
F(x) = 1 при x> 1,
равно…
+ 0
- 16/9
- 1
- 8/3
- 64/81
№18
24.1.2./18
УС 1
АБ
Время: 1 мин.
Постоянный параметр C в плотности распределения f(x)= 2 C /(1+ x 2)непрерывной случайной величины X, заданной на всей оси Ox, равен…
+ 1/2
- π/2
- 1
- π
|
|
|


