Практические задания для контрольной работы

Методы оптимальных решений

Методы принятия управленческих решений

 

 

Курган – 2013
Т.В. Полушкина, М.И. Цисарева

 

 

Методы оптимальных решений

Методы принятия управленческих решений

Методические указания и задания для выполнения контрольных работ

студентов 3 курса заочного отделения направлений подготовки

080100 – Экономика, 080200 - Менеджмент

 

 

Курган – 2013

УДК 519.85(07)

ББК У9(2)210.301(я7)

П 53

 

Полушкина Т.В., Цисарева М.И. Методы оптимальных решений. Методы принятия управленческих решений: методические указания и задания для выполнения контрольных работ студентов 3 курса заочного отделения направлений подготовки 080100 – Экономика, 080200 - Менеджмент.- Курган: изд-во КГСХА, 2013.- 41 с.

 

 

Рецензент: кандидат физико-математических наук, доцент Московченко Г.А.

 

Методические указания подготовлены в соответствии с государственным образовательным стандартом и программами дисциплин «Методы оптимальных решений», «Методы принятия управленческих решений». Предназначены для студентов 3 курса заочного отделения направлений подготовки 080100 – Экономика, 080200 - Менеджмент.

Методические указания рассмотрены и одобрены на заседании кафедры вычислительной техники и информатики (протокол № 2 от 10 сентября 2012 г.), утверждены и рекомендованы к изданию методической комиссией экономического факультета (протокол № 4 от 28.02.2013 г.).

 

© ФГБОУ ВПО «Курганская
государственная сельскохозяйственная академия имени Т.С. Мальцева», 2013

ВВЕДЕНИЕ

 

В мировой практике давно признано, что необходимым условием развития экономической науки является применение точных методов количественного анализа. В условиях рыночной экономики увеличивается интерес у специалистов к научному решению проблем принятия экономических и управленческих решений с использованием экономико-математических методов и построенных на их основе моделей. Использование современных методов исследования экономических явлений и процессов позволяет полнее и глубже обосновывать темпы и пропорции развития на макро- и микроуровне, добиваться оптимума среди альтернативных решений. При этом возрастает роль экономико-математического моделирования как научного направления об измерениях в экономике и управлении с использованием современных экономико-математических методов, моделей и средств их реализации.

Целью освоения дисциплины является формирование у студентов теоретических знаний в области оптимизации производственных процессов и систем, а также приобретение навыков использования оптимизационных методов для принятия эффективных управленческих решений.

Задачи дисциплины:

- раскрыть содержание основных понятий и категорий методов оптимальных решений;

- познакомить с основными методами решения экономико-мате­ма­ти­чес­ких моделей с помощью прикладного программного обеспечения;

- научить составлять стандартные теоретические модели исследуемых процессов, явлений и объектов, относящихся к области профессиональной деятельности, анализировать и интерпретировать полученные решения.

В результате освоения дисциплины студент должен:

знать: теоретические и методологические основы методов оптимальных решений;

уметь: моделировать социально-экономические системы, процессы, решать задачи на ЭВМ, используя современное программное обеспечение;

владеть: навыками применения современного математического инструментария для решения экономических задач, методикой построения, анализа и применения математических моделей для оценки состояния и прогноза развития экономических явлений и процессов.

Выполнение контрольной работы позволит студентам ознакомиться с основными оптимизационными методами решения экономико-мате­ма­ти­чес­ких задач.

ОБЩИЕ ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

Контрольная работа состоит из двух частей. В первой части работы должен быть дан ответ на теоретический вопрос. Во второй части работы должно быть выполнено практическое задание.

Контрольная работа должна иметь следующую структуру:

1. Титульный лист

2. Содержание

3. Теоретический вопрос

4. Практическое задание

5. Список литературы

Титульный лист контрольной работы должен содержать все необходимые реквизиты: названия академии и факультета; наименование учебной дисциплины; номер группы и номер зачетной книжки, Ф.И.О. студента.

Работа без указания номера зачетной книжки проверке не подлежит.

Номер вопроса для выполнения первой части работы определяется студентом по таблице 1 на пересечении последней и предпоследней цифр шифра (номера зачетной книжки).

Ответ на теоретический вопрос должен быть отпечатан на компьютере с соблюдением стандарта по оформлению печатных документов:

­ поля верхнее и нижнее -20 мм, левое – 30 мм, правое – 10 мм;

­ интервал между строками – полуторный;

­ обязателен перенос слов по слогам;

­ выравнивание – по ширине;

­ шрифт предпочтительно Times New Roman, 14 пт.;

­ количество символов в строке 65-70.

Номера задач для выполнения второй части контрольной работы определяются студентом по последней цифре номера зачётной книжки. Решение задач должно сопровождаться необходимыми комментариями, т.е. все основные моменты процесса решения задачи должны быть раскрыты и обоснованы соответствующими теоретическими положениями.

В конце работы должна быть указана дата выполнения и поставлена подпись исполнителя.

К собеседованию допускаются студенты, выполнившие правильно и в полном объеме все задания контрольной работы.

Для получения зачета по результатам собеседования студент должен знать теоретические основы тематики задач контрольной работы и уметь ответить на конкретные вопросы по содержанию проверенной работы.

ВОПРОСЫ К ТЕОРЕТИЧЕСКОЙ ЧАСТИ КОНТРОЛЬНОЙ РАБОТЫ

 

Таблица 1 – Варианты вопросов к контрольной работе

Предпоследняя цифра	Последняя цифра номера зачётной книжки

 

1. Математическое программирование и его основные задачи.

2. Понятие модели и моделирования. Экономико-математическая модель.

3. Преимущества моделирования.

4. Методы экономико-математического моделирования.

5. Линейное программирование и его основные методы.

6. Условия, допускающие применение методов линейного программирования.

7. Общая задача линейного программирования и ее математическая модель.

8. Условные обозначения, применяемые при моделировании.

9. Объекты планирования в экономико-математической модели. Основное требование к переменным.

10. Система переменных величин: основные, дополнительные, вспомогательные.

11. Типы ограничений, применяемые при моделировании. Система ограничений.

12. Понятие критерия оптимальности и его запись в экономико-матема­ти­­­чес­кой модели.

13. Формы записи экономико-математических моделей: структурная, развёрнутая, матричная.

14. Процесс построения экономико-математической модели.

15. Сущность графического метода линейного программирования.

16. Возможные области допустимых решений в графическом методе. Многоугольник решений.

17. Сущность симплексного метода линейного программирования. Математическая модель задач, решаемых симплексным методом.

18. Стандартная задача линейного программирования и приведение её к каноническому виду.

19. Понятие базисных и свободных переменных в линейном программировании.

20. Алгоритм решения задачи линейного программирования симплексным методом.

21. Допустимое и оптимальное решения.

22. Оптимальный план задачи. Содержание последней симплексной таблицы.

23. Анализ моделей на чувствительность.

24. Двойственные оценки и их свойства.

25. Двойственные задачи линейного программирования.

26. Транспортная задача линейного программирования, её модель.

27. Основные особенности транспортной задачи. Открытая и закрытая транспортные задачи.

28. Методы получения опорного плана в транспортной задаче.

29. Методы решения транспортной задачи.

30. Алгоритм решения транспортной задачи распределительным методом.

31. Алгоритм решения транспортной задачи методом потенциалов.

32. Усложнённые задачи транспортного вида.

33. Понятие неопределенности и основные источники её возникновения.

34. Ситуация риска и сопутствующие ей условия. Экономический риск.

35. Методы принятия решений в условиях полной определённости.

36. Нормализация критериев в задачах принятия решений в условиях полной определённости.

37. Критерии оценки принимаемых решений в условиях риска.

38. Принятие решений в условиях неопределенности с использованием критерия Лапласа.

39. Принятие решений в условиях неопределенности с использованием критерия Вальда.

40. Принятие решений в условиях неопределенности с использованием критерия Сэвиджа.

41. Принятие решений в условиях неопределенности с использованием критерия Гурвица.

42. Ситуации, изучаемые в теории игр. Понятие игры.

43. Стратегия игры. Матричные игры, разрешимые в чистых стратегиях.

44. Смешанные стратегии. Матричные игры в смешанных стратегиях.

45. Оптимальные стратегии. Решение игры.

46. Матричная игра двух партнёров с нулевой суммой и используемые в ней критерии.

47. Принцип минимакса и минимаксной чистой стратегии в теории игр.

48. Основные методы нелинейного программирования.

49. Динамическое программирование.

50. Стохастическое программирование.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ ЗАДАНИЙ КОНТРОЛЬНОЙ РАБОТЫ

ОСНОВНЫЕ ТЕРМИНЫ

 

Математическое программирование - это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Термин «программирование» заимствован из зарубежной литературы, где он используется в смысле "планирование".

Экономико-математические методы:

­ линейное и целочисленное программирование;

­ математическая теория оптимального управления; матричные игры; кооперативные игры; игры с природой;

­ сетевые графики;

­ марковские процессы;

­ задачи анализа замкнутых и разомкнутых систем массового обслуживания;

­ динамическое программирование

Наиболее простыми и лучше всего изученными среди задач математического программирования являются задачи линейного программирования. Линейное программирование рассматривает методы решения математических моделей, содержащих уравнения или неравенства первой степени.

Характерные черты задач линейного программирования следующие:

1) показатель эффективности F представляет собой линейную функцию от элементов решения ;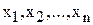

2) ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств.

Экономико-математическая модель - это математическое описание экономического явления или процесса с целью его исследования и управления.

Оптимизационная модель позволяет из нескольких альтернативных вариантов выбрать наилучший вариант по любому признаку.

Методы оптимизации: графический, симплексный, распределительный, потенциалов и др.

Критерий оптимальности – показатель, количественно выражающий предельную меру экономического эффекта от принимаемого хозяйственного решения.

 

В общей форме записи модель задачи линейного программирования имеет следующий вид.

Целевая функция (ЦФ):

при ограничениях

(1)

где	- переменные величины (объекты планирования)
	- технико-экономические коэффициенты при переменных в ограничениях
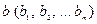
	- объёмы ограничений
	- коэффициенты при переменных в целевом уравнении

Допустимое решение (или план) - это совокупность чисел , удовлетворяющих ограничениям задачи (1).

Оптимальный план - это план , при котором ЦФ принимает свое максимальное (минимальное) значение.

Модели и методы линейного программирования успешно применяются при решении задач в таких сферах, как промышленное производство, военное дело, сельское хозяйство, экономические исследования, транспорт, здравоохранение, психология, социальные науки.

ПОСТРОЕНИЕ МОДЕЛЕЙ ОДНОИНДЕКСНЫХ ЗАДАЧ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ

Для построения математической модели необходимо ответить на следующие три вопроса:

1) Как идентифицировать искомые величины, т.е. переменные этой задачи?

2) В чем состоит цель, для достижения которой из всех допустимых значений переменных нужно выбрать те, которые будут соответствовать наилучшему, т.е. оптимальному решению?

3) Какие ограничения должны быть наложены на переменные, чтобы выполнялись условия, описанные в задаче?

Пример 1. Небольшая фабрика производит два вида красок: первый - для наружных, а второй - для внутренних работ. Продукция обоих видов поступает в оптовую продажу. Для производства красок используются два ингредиента - А и В. Максимально возможные суточные запасы этих ингредиентов составляют 6 и 8 ц соответственно. Расходы А и В на 1 т соответствующих красок приведены в таблице 2.

Таблица 2 - Исходные данные к задаче

Ингредиенты	Расход ингредиентов на тонну краски, ц	Максимально возможный запас, т
краска 1-го вида	краска 2-го вида
А
В

Изучение рынка сбыта показало, что суточный спрос на краску 2-го вида никогда не превышает спроса на краску 1-го вида более, чем на 1 т. Кроме того, установлено, что спрос на краску 1-го вида никогда не превышает 2 т в сутки.

Оптовые цены одной тонны красок равны: 3 тыс.р. для краски 1-го вида; 2 тыс.р. для краски 2-го вида.

Необходимо установить какое количество краски каждого вида должна производить фабрика, чтобы выручка от реализации продукции была максимальной.

Переменные

Поскольку в задаче требуется определить объемы производства каждого вида красок, то эти объемы и будут являться переменными модели, а именно:

- суточный объем производства краски 1-го вида, т

- суточный объем производства краски 2-го вида, т

Целевая функция

В условии задачи сформулирована цель - добиться максимальной выручки от реализации продукции. Суточная выручка от продажи краски 1-го вида равна тыс.р., а от продажи краски 2-го вида - тыс.р. Поэтому целевой функцией будет математическое выражение, в котором суммируется выручка от продажи красок 1-го и 2-го видов (при допущении независимости объемов сбыта каждой из красок).

.

Ограничения

Ограничения, налагаемые на возможные объемы производства красок, т.е. на переменные и , обуславливаются:

­ количеством расходуемых ингредиентов A и B;

­ данными о спросе на каждый вид краски.

Ограничения на расход содержательно можно записать в виде:

,

а математически - в виде:

1. х₁+2х₂≤6 - по использованию ингредиента А, ц

2. 2х₁+х₂≤8 - по использованию ингредиента В, ц

Примечание: при математической записи ограничений следует всегда проверять размерность левой и правой частей каждого из ограничений. Несовпадение этих размерностей свидетельствует о принципиальной ошибке.

Ограничения по спросу на каждый вид краски содержательно можно записать в виде:

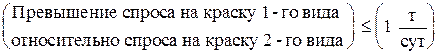и

,

Математически это выглядит так:

3. -х₁+х₂ ≤ 1 - По спросу на краску 2-го вида, т

4. х₁ ≤ 2 - По спросу на краску 1-го вида, т

При этом подразумевается, что объемы производства не могут принимать отрицательных значений, что записывается как

.

Таким образом, математическая модель этой задачи имеет вид

ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Графический метод позволяет найти решение задачи линейного программирования с двумя переменными. Для трех переменных графическое решение становится менее наглядным, а для большего числа переменных необходимо применение алгебраического аппарата.

Этапы графического метода:

1 Получить уравнения прямых путем замены в ограничениях задачи знаков неравенств на знаки точных равенств и построить эти прямые.

2 Найти и заштриховать полуплоскости, определяемые и разрешаемые каждым из ограничений-неравенств задачи. Для этого необходимо:

­ подставить в конкретное неравенство координаты какой-либо точки, например, (0;0) и после этого проверить истинность полученного неравенства;

­ если неравенство истинное, то заштриховать полуплоскость, содержащую точку (0;0);

­ иначе (неравенство ложное) заштриховать полуплоскость, не содержащую точку (0;0);

­ поскольку и должны быть неотрицательными, то их допустимые значения всегда будут находится выше оси и правее оси , т.е. в 1-м квадранте.

Ограничения-равенства разрешают только те точки, которые лежат на соответствующей прямой.

3 Определить область допустимых решений (ОДР) как часть плоскости, принадлежащую одновременно всем разрешенным областям, и заштриховать ее.

4 Построить прямую целевой функции (ЦФ) , проходящую через ОДР. Для этого надо построить прямую, произвольно выбрав F (удобно использовать в качестве F число, кратное коэффициентам целевой функции). Произвольный выбор F связан с тем, что, придавая F различные значения, мы будем получать различные прямые, параллельные друг другу. При этом будет изменяться лишь длина отрезка, отсекаемого прямой на оси (начальная ордината), а угловой коэффициент прямой, равный будет оставаться постоянным.

5 Построить вектор , который начинается в точке (0;0) и заканчивается в точке . Вектор показывает направление возрастания значений ЦФ, а значит и значений F целевой прямой.

6 Передвигать целевую прямую:

­ в направлении вектора при поиске max ЦФ;

­ или в направлении, противоположном вектору , при поиске min ЦФ.

В результате этого передвижения

­ найти точку (или точки), в которой ЦФ принимает max (или min) значение;

­ или установить, что ЦФ неограниченна на множестве планов сверху или снизу.

Оптимальное решение не может находиться внутри ОДР, а только на ее границе, а именно, в последней вершине многоугольника, через которую пройдет целевая прямая, или на всей его стороне. Допустимое решение, лежащее в вершине ОДР, называется опорным решением (планом).

7 Определить координаты точки максимума (минимума) ЦФ. Для точного определения координат оптимальной точки необходимо решить систему уравнений прямых, на пересечении которых находится .

8 Вычислить значение ЦФ в точке максимума (минимума).

Пример 2. (см.условие примера1):

1) Построим следующие прямые (рисунок 1)

Для этого вычислим координаты точек пересечения этих прямых с осями координат

(1) - (2); - (3) -

2-3) После проведения штриховки допустимых полуплоскостей определяем, что ОДР - это многоугольник ABCDEF.

4) Целевую прямую можно построить по уравнению

,

5) Построить вектор , который начинается в точке (0;0) и заканчивается в точке(3,2). Если целевая прямая и вектор построены верно, то они будут перпендикулярны.

6) Точка Е - это последняя вершина многоугольника допустимых решений, через которую проходит целевая прямая, двигаясь по направлению вектора , т.е. т.Е - это точка максимума ЦФ.

7) Координаты точки Е, найдем как решение системы уравнений для прямых 1 и 2.

,

Точка максимума (max)

8) Таким образом, максимальное значение ЦФ равно:

 

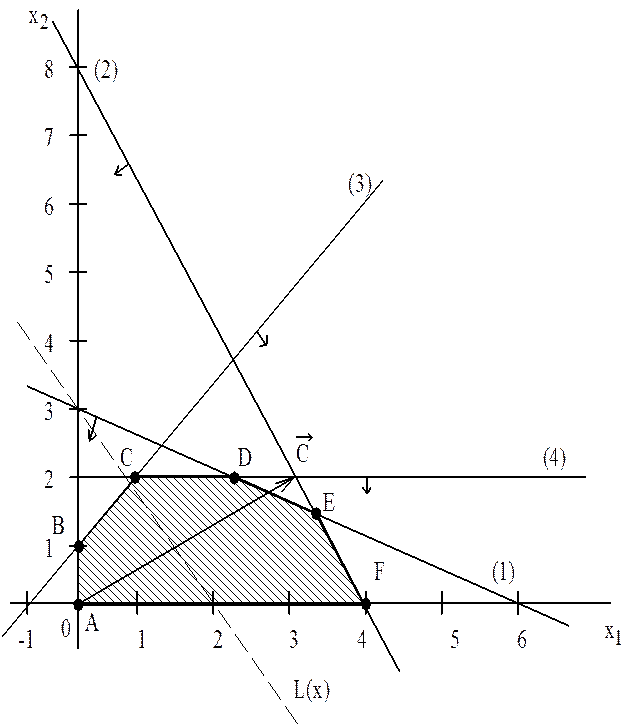
Рисунок 1- График решения задачи

СИМПЛЕКС-МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

 

Симплексный метод основан на последовательном переходе от одного опорного плана задачи линейного программирования к другому. При этом значение целевой функции на каждой итерации улучшается, пока не достигнет оптимума.

Рассмотрим алгоритм симплексного метода на примере задачи планирования товарооборота.

Пример 3. Коммерческое предприятие, располагающее производственными ресурсами, реализует три группы товара А, В и С. Плановые нормативы затрат ресурсов на 1 тыс. р. товарооборота, доход от продажи товаров на 1 тыс. р. товарооборота, а также объем ресурсов заданы в таблице 3.

Таблица 3 – Параметры задачи

Показатели	Норма затрат производственных ресурсов на 1 тыс. р. товарооборота	Объем ресурсов (вi)
группа А	группа В	группа С
Ресурсы первого вида, усл. ед.	0,1	0,2	0,4	1 100
Ресурсы второго вида, усл. ед	0,05	0,02	0,02
Ресурсы второго вида, усл. ед				8 000
Доход, ден. ед. (Сj)				mах

Необходимо определить плановый объем продажи и структуру товарооборота, при которых доход торгового предприятия будет максимальным.

Составим экономико-математическую модель задачи.

Переменные:

х₁ – количество товаров группы А, ед.

х₂ – количество товаров группы В, ед.

х₃ – количество товаров группы С, ед.

Ограничения:

1) По использованию ресурсов первого вида, усл. ед.

0,1х₁ + 0,2х₂ + 0,4х₃ 1100

2) По использованию ресурсов второго вида, усл. ед.

0,05х₁ + 0,02х₂ + 0,02х₃ 120

3) По использованию ресурсов третьего вида, усл. ед.

3х₁ + х₂ + 2х₃ 8000

4) Условие не отрицательности переменных

х₁ 0, х₂ 0, х₃ 0.

Максимальное значение целевой функции, ден.ед.

F(х) = 3х₁ + 5х₂ + 4х₃ mах

Алгоритм симплексного метода включает следующие этапы:

1 Составление первого опорного плана

Система ограничений задачи, решаемой симплексным методом задана в виде неравенств смысла “ ”, правые части которых в_i 0. Перейдем от системы неравенств к системе уравнений путем введения неотрицательных дополнительных переменных х₄; х₅; х₆; которые образуют базис и называются базисными переменными. Они определяют объемы неиспользованных ресурсов:

0,1х₁ + 0,2х₂ + 0,4х₃ + х₄ = 1100

0,05х₁ + 0,02х₂ + 0,02х₃ + х₅ = 120

3х₁ + х₂ + 2х₃ + х₆ = 8000

Решим систему уравнений относительно базисных переменных:

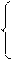х₄ = 1100 – (0,1х₁ + 0,2х₂ + 0,4х₃)

х₅ = 120 – (0,05х₁ + 0,02х₂ + 0,02х₃)

х₆ = 8000 – (3х₁ + х₂ + 3х₃)

Функцию цели запишем в виде уравнения F(х) = 0 – (– 3х₁ – 5х₂ – 4х₃).

Получим первый опорный план. Предположим, что основные переменные в системе уравнений являются свободными и приравняем их к нулю (х₁=0 х₂=0 х₃=0). Тогда дополнительные переменные (базисные) будут равны объёмам ограничений (х₄=1100; х₅=120; х₆=800). Следовательно, товары не продаются, а ресурсы не используются, доход равен нулю: f(x)=0. Заносим этот план в первую симплексную таблицу. Она состоит из коэффициентов системы ограничений и свободных членов. Последняя строка таблицы называется индексной и заполняется коэффициентами функции цели, взятыми с противоположными знаками.

Таблица 4 - Первая симплексная таблица

План	Базисные переменные	Свободные члены	Основные переменные	Дополнительные переменные
х1	х2	х3	х4	х5	х6
I	х4		0,1	0,2	0,4
х5		0,05	0,02	0,02
х6
Индексная строка	f(x)		-3	-5	-4

2 Проверка плана на оптимальность

Если все коэффициенты индексной строки симплексной таблицы при решении задачи на максимум неотрицательны ( 0), то план является оптимальным. Если найдется хотя бы один коэффициент индексной строки меньше нуля, то план не является оптимальным и его можно улучшить.

Опорный план, представленный в первой симплексной таблице, не оптимальный, т.к. в индексной строке находятся отрицательные коэффициенты: -3; -5; -4.

В этом случае переходим к следующему этапу алгоритма.

 

3 Определение ведущих столбца и строки

Из отрицательных коэффициентов индексной строки выбираем наибольший по абсолютной величине, что и определяет ведущий столбец, который показывает, какая переменная на следующей итерации перейдет из свободных в базисные. За ведущий столбец выберем столбец, соответствующий переменной х_2, сравнивания по модулю |- 5 | >|- 3 |; |- 4 |. Выделим его в таблице 5.

Таблица 5 - Первая симплексная таблица

План	Базисные переменные	Свободные члены	Основные переменные	Дополнительные переменные
х1	х2	х3	х4	х5	х6
I	х4		0,1	0,2	0,4
х5		0,05	0,02	0,02
х6
Индексная строка	f(x)		-3	-5	-4

Затем элементы столбца свободных членов симплексной таблицы делим на положительные элементы ведущего столбца. Результаты заносим в дополнительный столбец _i.

Строка симплексной таблицы, соответствующая минимальному значению _i, является ведущей. Она определяет переменную х _i, которая на следующей итерации выйдет из базиса и станет свободной.

Вычислим значения _i по строкам и выберем наименьшее отношение: 1100/0,2 = 5500(min); 120/0,02=6000; 8000/1=8000; следовательно, строка х₄ является ведущей. Выделим её в таблице (таблица 6).

 

 

Таблица 6 - Первая симплексная таблица

План	Базисные переменные	Свободные члены	Основные переменные	Дополнительные переменные	i
х1	х2	х3	х4	х5	х6
I	х4		0,1	0,2	0,4
х5		0,05	0,02	0,02
х6
Индексная строка	f(x)		-3	-5	-4				Х

Элемент симплексной таблицы, находящийся на пересечении ведущих столбца и строки, называют разрешающим. Разрешающий элемент равен 0,2.

4 Построение нового плана

Переход к новому плану осуществляется в результате пересчета симплексной таблицы методом Жордана-Гаусса. Сначала заменим переменные в базисе, т.е. вместо (х _i =х₄) в базис войдет переменная (х _j= х₂) соответствующая ведущему столбцу.

1. Разделим все элементы ведущей строки предыдущей симплексной таблицы на разрешающий элемент и результаты деления занесем в начальную строку следующей симплексной таблицы, т.е.

(х₂): 1100/0,2=5500; 0,1/0,2=0,5; 0,2/0,2=1;0,4/0,2=2;1/0,2=5.

2. Коэффициенты всех последующих строк определяются по формуле:

(новый коэффициент) = (соответствующий коэфф. предыдущей табл.)–(коэффициент ведущего столбца) х (коэффициент начальной строки)

Например, новое значение свободного члена по строке х₅ будет

120 - 0,02 * 5500 = 10

Выполняя последовательно все этапы алгоритма, формируем план 2.

Таблица 7 - Вторая симплексная таблица

План	Базисные переменные	Свободные члены	Основные переменные	Дополнительные переменные	2
х1	х2	х3	х4	х5	х6
II	х2		0,5
х5		0,04		-0,02	-0,1
х6		2,5			-5
Индексная строка	f(x2)	27 500	-0,5						Х

 

5 Анализ второго плана: Доход в размере 27500 ден.ед. торговое предприятие получит от продажи товаров группы В (х₂) в количестве 5500 ед. Среди базисных переменных находится дополнительные переменные х₅ и х₆. Это указывает на то, что ресурсы второго вида недоиспользована на 10 усл.ед. и ресурсы третьего вида недоиспользованы на 2500 усл.ед . План не оптимальный т.к. в индексной строке имеется отрицательный коэффициент (-0,5).

Вычислительный процесс повторяется, начиная с пункта 3 алгоритма, до получения оптимального плана.

На третьей итерации получаем план 3, который является оптимальным, т.к. все коэффициенты в индексной строке 0.

Таблица 8 - Третья симплексная таблица

План	Базисные переменные	Свободные члены	Основные переменные	Дополнительные переменные	2
х1	х2	х3	х4	х5	х6
III	х2				2.25	6,25	12,5		-
х1				0,5	-2,5			-
х6				1,25	1,25	62,5		-
Индексная строка	F(x3)	27 625			5,75	23,75	12,5		Х

 

6 Анализ третьего плана: Необходимо продавать товаров группы А в количестве 250 ед. и группы В - в количестве 5375 ед. Товары группы С не реализуются. При этом торговое предприятие получает максимальный доход в размере 27625 ден.ед.

В оптимальном плане среди базисных переменных находится дополнительная переменная х₆. Это указывает, что ресурсы третьего вида недоиспользованы на 1875 усл.ед., т.к. переменная х₆ была введена в третье ограничение задачи, характеризующее собой недоиспользование ресурсов третьего вида.

ТРАНСПОРТНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Стандартная транспортная задача определяется как задача разработки наиболее экономичного плана перевозки продукции однородного груза из нескольких пунктов отправления в несколько пунктов назначения. При этом величина транспортных расходов прямо пропорциональна объему перевозимой продукции и задается с помощью тарифов на перевозку единицы продукции.

Целевая функция представляет собой общие транспортные расходы на осуществление всего объёма перевозок.

Первая группа (1) ограниче

Поделиться:

Воспользуйтесь поиском по сайту: