 |
Устройство лабораторной установки
|
|
|
|
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА
ВЯЗКОСТИ ЖИДКОСТИ МЕТОДОМ СТОКСА
Цель работы: определение коэффициента вязкости жидкости методом Стокса.
Приборы и принадлежности: стеклянный цилиндр, наполненный глицерином, металлический шарик, секундомер, линейка, штангенциркуль.
Общие указания
При течении газа или жидкости между смежными слоями возникают силы внутреннего трения, действие которых препятствует взаимному перемещению слоев. Свойство газа или жидкости оказывать сопротивление перемещению одних слоев относительно других называется вязкостью.
Если в потоке газа или жидкости мысленно выделить два смежных слоя
|
| Рис.1 |
1 и 2 (рис.1), скорости, движения которых соответственно равны υ и υ+dυ, то силы внутреннего трения действуют на каждый из слоев: на слой 2 (скорость его больше) действующая сила направ-лена противоположно движению слоя, а на слой 1 – в направлении движения. Действие этих сил способствует выравниванию скоростей движения слоев, т.е. препятствует движению потока газа или жидкости в целом. Величина силы внутреннего трения F, возникающая между двумя смежными слоями, пропорциональна площади ΔS их соприкосновения и градиенту скорости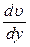 
в направлении, перпендикулярном вектору скорости:
,
где η – коэффициент внутреннего трения или динамическая вязкость.
Коэффициент вязкости η – величина, равная силе внутреннего трения, приложенной к каждой единице поверхности соприкосновения двух слоев, движущихся друг относительно друга с градиентом скорости, равным единице. В СИ коэффициент вязкости η измеряется в Па·с.
Возникновение внутреннего трения в газах или жидкостях обусловлено несколькими различными причинами.
|
|
|
В газах, где среднее расстояние между молекулами в тысячи раз превышает размеры молекул, силы взаимодействия между молекулами настолько малы, что движение молекул от столкновения до столкновения происходит по прямой. Возникновение силы внутреннего трения в газах обусловлено только взаимным проникновением молекул из одного слоя в другой. В изображенном на рис.1 случае, молекулы, проникшие из более быстрого слоя 2 в слой 1, передают некоторый импульс молекулам этого слоя. Это равносильно действию на слой 1 некоторой силы в направлении его движения. В свою очередь молекулы, проникшие из более медленного слоя 1 в слой 2, получают некоторый импульс, что приводит к торможению слоя 2, а это равносильно действию силы F в направлении, противоположном движению. Поскольку количество молекул, проникающих из слоя 1 в слой 2 и наоборот, в среднем одинаково, а переносимый ими импульс разный (скорости слоев разные), в явлении внутреннего трения в газах происходит направленный перенос импульса молекул в направлении от более быстрого слоя к более медленному (от слоя 2 к слою 1). Поэтому явление внутреннего трения наряду с диффузией и теплопроводностью относится к явлениям переноса.
Следует помнить, что коэффициент вязкости дня газов возрастает с повышением температуры (η ~ 
). Это объясняется тем, что с повышением температуры газа увеличивается скорость теплового движения молекул, что способствует более интенсивному обмену молекул между слоями и приводит к увеличению направленного переноса импульса молекул, т.е. к увеличению вязкости.
В жидкостях, плотности которых в тысячи раз превышают плотность газа, среднее расстояние между молекулами сравнимо с их размерами. Поэтому силами взаимодействия между молекулами в жидкостях пренебрегать нельзя, и они сказываются при взаимном перемещении одних молекул относительно других. Кроме того, молекулы жидкости (в отличие от молекул газа) совершают колебательное движение относительно временных положений равновесия, меняя их через некоторые промежутки времени. Чем ниже температура жидкости, тем реже молекулы изменяют свои положения равновесия, и смещение одних молекул относительно других затруднено. Поэтому и вязкость жидкости при понижении температуры возрастает. Таким образом, вязкость в жидкостях обусловлена взаимодействием молекул и особым характером их теплового движения.
|
|
|
Устройство лабораторной установки
|
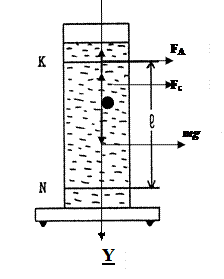
| Рис.2. |
Для определения вязкости приме-няется прибор, представляющий собой стеклянный цилиндр (рис.2), наполненный вязкой жидкостью (глицерином). На боковой поверхности цилиндра нанесены две горизонтальные метки К и N рас-положенные на расстоянии l друг от друга. Метка К помещена на некотором рас-стоянии от верхнего уровня жидкости. Положение этой метки подобрано таким образом, чтобы шарик, свободно падая в жидкости и между метками, двигался равномерно.
Вывод рабочей формулы
Одним из способов определения коэффициента вязкости жидкости является метод Стокса. Он основан на определении силы сопротивления, действующей на свободно падающий в жидкости металлический шарик.
На шарик, падающий в жидкости, действуют три силы: сила тяжести 
=mg, сила вязкого трения (сопротивления) 
и выталкивающая сила 
(архимедова сила). С увеличением скорости сила сопротивления возрастает и с некоторого момента шарик станет двигаться равномерно. Условие равномерного падения шарика в жидкости
.
Свяжем ось OУ с направлением движения шарика. Тогда уравнение движения шарика в проекции на эту ось принимает вид:
P - Fc - Fa= 0
При движении шарика в жидкости играет роль трение отдельных слоев жидкости друг о друга, так как ближайший к поверхности шарика слой жидкости имеет ту же скорость, что и шарик – жидкость прилипает к нему. Другие же слои имеют тем меньшую скорость, чем дальше находятся они от шарика. Поэтому сила сопротивления движению шарика будет зависеть не только от его скорости и размеров, но и от вязкости жидкости.
По закону Стокса сила сопротивления прямо пропорциональна первой степени скорости, коэффициенту вязкости и линейным размерам тела. Для шара движущегося в вязкой жидкости, по закону Стокса сила сопротивления
|
|
|
Fc = 6π η r υ,
где η – коэффициент вязкости жидкости; r – радиус шара; υ – скорость его движения.
Выряжая массу шарика и выталкивающую силу через соответствующие плотности, и размеры шарика, а также скорость шарика через пройденный путь и время, получим рабочую формулу
| (1) |
где ρ – плотность шарика (ρ =7800 кг/м3); ρж – плотность жидкости (ρж =1260 кг/м3); d – диаметр шарика; t – время движения шарика; l – путь, пройденный шариком за время t при равномерном движении; g – ускорение свободного падения.
Порядок выполнения работы
1. Бросьте шарик в цилиндрический сосуд (рис.2) и определить на глаз точку, начиная с которой шарик начинает двигаться равномерно. Установить верхнюю метку на 2-3 см ниже этой точки. Рулеткой или линейкой измерить расстояние между верхней К и нижней N метками.
2. Микрометром измерить диаметр d стального шарика. Измерение повторить не менее пяти раз в разных направлениях.
3. Опустить шарик в жидкость в центре цилиндра и внимательно следить за его прохождением мимо метки К. Глаз при этом должен фиксировать совпадение метки по всей окружности цилиндра. Включить секундомер в момент прохождения шариком метки К и выключить его в момент прохождения шариком метки N. Показания секундомера занести в таблицу. Шарик вытащить из жидкости при помощи магнита. Опыт повторить 5 раз.
Таблица 1.
Результаты записать в таблицу
| № п.п. | l, м | d, м | t, с | η,кг/м·с | Δη,кг/м·с | ε, % |
| Середнее значение |
Обработка результатов
1. По формуле (1) вычислить значение η, подставляя значения d и l. Данные занести в таблицу 1.
2. Определить среднее значение измеренных величин.
3. Определить среднее значение коэффициента вязкости:
.
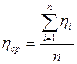4. Определить абсолютною погрешность отдельного косвенного измерения:
|
|
|
,
где Δd = 0,01 мм; Δl = 0,5 мм; Δt = 0,01 с.
5. Определить среднее значение абсолютной погрешности:
.
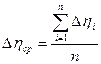6. Подсчитать относительную погрешность измерения:
.
7. Полученный результат представить в виде
ηист=ηср±Δηср.
Контрольные вопросы
1. Запишите формулу для силы вязкого трения.
2. Какой физический смысл имеет коэффициент вязкости?
3. Как зависит коэффициент внутреннего трения газов и жидкостей
от температуры? Объясните эту зависимость на основе молекулярно-кинетической теории строения вещества.
4. В чем различие механизма возникновения внутреннего трения в газах и жидкостях?
5. Объясните механизм возникновения силы внутреннего трения, действующей на шарик, который движется в вязкой среде.
6. Как изменяется скорость шарика при падении в жидкости?
8. Выведите формулу для расчета коэффициента вязкости.
9. В чем сущность использованного в работе определения вязкости.
|
|
|
