 |
Определение параметров восстановления
|
|
|
|
ЭиТС НАП
Типы задач и методические указания к их решениям.
Типы задач МК-2
1. Сигнал x(t) случаен и стационарен, подвергается аналого-цифровому преобразованию способом замены его мгновенных значений ближайшим уровнем квантования. Сигнал задан функцией плотности вероятности f(x). Аналого-цифровой преобразователь имеет диапазон входных сигналов – L, разрядность выходного двоичного кода – n. Определить среднее значение погрешности квантования.

2. Сигнал x(t) подвергается аналого-цифровому преобразованию способом замены его мгновенных значений ближайшим меньшим уровнем квантования. Установить число разрядов выходного двоичного кода АЦП. Сигнал случаен и стационарен, задан функцией плотности вероятности f(x). Величина дисперсии погрешности квантования не должна превысить Dd _ 10-6Dx, где Dx — дисперсия сигнала.

3. Случайный стационарный сигнал x(t) со средним значением mx = 0, задан корреляционной функцией Rxx(t); дискретизируется с постоянным шагом и каждый отсчет подвергается аналого-цифровому преобразованию способом замены его мгновенных значений ближайшим большим уровнем квантования.. Установить число разрядов выходного двоичного кода АЦП., если величина среднеквадратичной погрешности квантования, не должна превысить величины Dd _ 10-6Dx, где Dx — дисперсия сигнала.
 ;–ђ<t<ђ;
;–ђ<t<ђ; 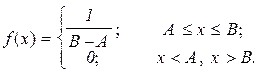
4. Случайный стационарный сигнал x(t), задан корреляционной функцией Rxx(t), дискретизируется с постоянным шагом Dt. По дискретным отсчетам сигнал восстанавливается цифро-аналоговым преобразователем. Оценить величину шага дискретизации Dt, если величина среднеквадратичной погрешности восстановления, не должна превысить величины y2 £ 0,05Dx, где Dx — дисперсия сигнала.
|
|
|
 ; –ђ<t<ђ;
; –ђ<t<ђ;
5. Случайный стационарный сигнал x(t), заданный спектральной плотностью средней мощности Sxx(w), дискретизируется с постоянным шагом Dt. Восстановление сигнала осуществляется идеальным низкочастотным фильтром. Установить величину шага дискретизации и полосы пропускания фильтра.

Методические указания к решению задач по теме
«Погрешности аналогово-цифрового преобразования»
1. Погрешности квантования (преобразования аналог-код) сигналов напряжения
– три способа квантования
I – замена аналоговой величины дискретной значением ближайшего меньшего уровня
xi < x(t) < xi+1 ® xi (1)
II – замена аналоговой величины дискретной значением ближайшего уровня
xi – Dx/2 < x(t) < xi + Dx/2 ® xi (2)
III – замена аналоговой величины дискретной значением ближайшего большего уровня
xi < x(t) < xi+1 ® xi+1 (3)
Погрешность квантования dк для трех методов имеет следующие функции плотности вероятности:

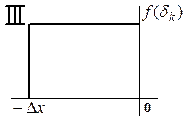
Определение статистических параметров погрешности квантования при известном значении шага квантования Dx:
– среднее значение погрешности квантования
 (4)
(4)
– дисперсия погрешности квантования
 (5)
(5)
– СКО погрешности квантования
 (6)
(6)
– среднее квадратическое значение погрешности квантования
 (7)
(7)
Все перечисленные статистические параметры выражаются (в виде функций) через значение шага квантования Dх, в том числе и функции плотности вероятности f(dк). Для определения (аналитического описания) этой функции следует воспользоваться соотношением:
 (8)
(8)
Определение параметров выходного кода преобразователя при известных значениях статистических параметров погрешности квантования (например, определение числа разрядов выходного дволичного кода)
– при известном значении статистического параметра погрешности квантования (md, Dd, sd, yd2) по функции j (Dх) определяется величина шага квантования Dх;
|
|
|
– из даннях о сигнале определяется диапазон его изменения [ xmin, xmax ]
– известна функция плотности вероятности f(dк)
– равномерный закон распределения

| xmin = А; xmax = В. |
– нормальный закон распределения плотности вероятности
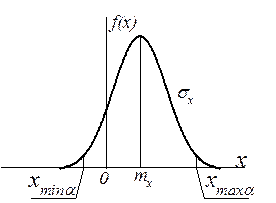
| xmin = xmina; xmax = xmaxa. [ xmina, xmaxa ] – доверительный интервал мгновенных значений х, при доверительной вероятности a; xmina = mx – za×sx; (9) xmax = mx + za×sx; (10) |
za – доверительная граница нормированного (табличного) распределения при доверительной вероятности a.
– требуемое количество уровней квантования определяется как
 (11)
(11)
– число разрядов к дволичного кода определяется из условия: число кодовых комбинаций двоичного кода должно бать не меньше числа уровней квантования
 (12)
(12)
Из неравенства устанавливается минимальное целое число к, удовлетворяющее неравенству.
– известен вид функции плотности вероятности, но неизвестны ее параметры; известны статистические параметры и характеристики сигнала. Например, сигнал имеет среднее mx, корреляционную функцию Rxx(t), функцию плотности вероятности f(x)

– неизвестные статистические параметры сигнала определяются на основании свойств функций
Rxx(t = 0) = Dx;
– параметры функции плотности вероятности А и В определяются из решения уравнения

– решая систему уравнений относительно А и В, определяют их значения;
– определяется число уровней квантования и число разрядов кода, как описано ранее.
Определение параметров восстановления
|
|
|


