 |
Расчет ТВС с холостым ходом теплоносителя
|
|
|
|
Расчет температурного режима в ТВС с кольцевыми твэлами.
Рассмотрим ТВС с кольцевым твэлом, охлаждаемым с двух сторон восходящим потоком теплоносителя (рис.4).
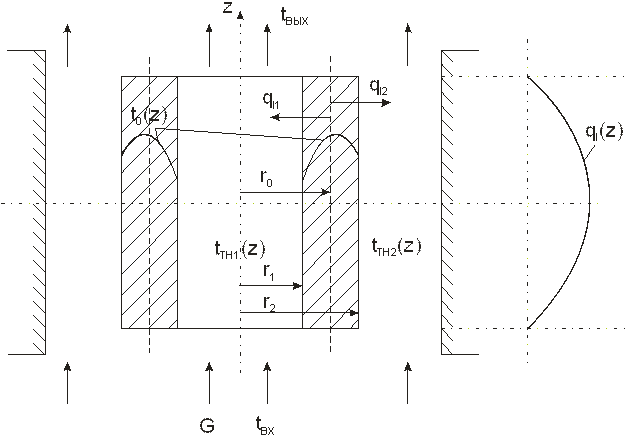
Рис. 4. Схема канала с кольцевым твэлом.
Теплоноситель общим расходом 
поступает на вход в канал с температурой 
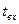, омывает кольцевой твэл с двух сторон и на выходе из твэла, после смешения имеет температуру 
. Т.к. отвод тепла от твэла двусторонний, внутри топливного сердечника образуется так называемая нейтральная поверхность, которая для любого сечения представляет собой окружность радиусом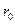 
, на которой температура сердечника максимальна. Тепловой поток при этом разделяется на два: 
- направленный внутрь твэла и 
- направленный наружу. На нейтральной поверхности тепловой поток равен нулю.
Нейтральный радиус 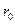в общем случае изменяется по высоте твэла, т.е. зависит от координаты 
, а температура теплоносителя во внутреннем канале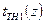 
не равна температуре 
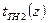во внешнем.
Будем полагать известными:
- размеры ТВС;
- температуры теплоносителя на входе и выходе твэла, соответственно , ;
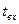- суммарный расход ;
- полный тепловой поток
.
Требуется определить:
- распределение температур теплоносителя во внутреннем 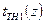и внешнем 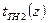каналах;
- распределение наружной температуры оболочки во внутреннем
и внешнем 
каналах; - распределение по высоте твэла максимальной температуры топлива
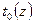, реализующейся на нейтральном радиусе 
.
Для любого сечения твэла по высоте справедливо соотношение:
, (82)
где 
и 
- полные перепады температуры: между максимальной температурой 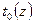(на нейтральном радиусе ) и температурами теплоносителя, протекающего во внутреннем 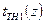и внешнем 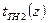каналах.
С учетом составляющих полного температурного перепада 
, (82) примет следующий вид:
|
|
|
, (83)
где 
и 
- тепловые периметры по теплоносителю, оболочке и газовому зазору во внутреннем и внешнем каналах соответственно; 
и 
- внутренний и наружный радиусы топливного сердечника кольцевого твэла; - нейтральный радиус.
Температурные перепады между максимальной и наружными температурами топливного сердечника, входящие в (83) получаются при решении уравнения теплопроводности с соответствующими граничными условиями.
Уравнение (83) содержит семь неизвестных: 
. Для их определения, необходимо записать дополнительные соотношения:
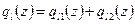; (84)
из условия 
, получим
(85)
для температуры теплоносителя, имеем
(86)
Распределение расхода теплоносителя на внутренний 
и внешний 
каналы, находится из условия равенства параметров давления:
, (87)
поскольку теплоноситель поступает в каналы из общего объема и выходит в общий объем. При использовании в качестве теплоносителя обычной воды, имеем
, (88)
где 
и 
- коэффициенты местных сопротивлений и сопротивления трения; 
и 
- высота и эквивалентный диаметр канала;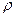 
и 
- средние плотность и скорость теплоносителя (ускорением потока пренебрегаем).
Равенство (87) дополняется условием
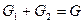(89)
После определения расходов и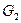 
, находятся средние скорости теплоносителя в соответствующих каналах 
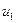и 
, рассчитываются коэффициенты теплоотдачи 
и 
. В результате, в уравнении (83) остается пять неизвестных, которые определяются с использованием соотношений (84)-(86). Если выразить в уравнении (83) все неизвестные через какую-нибудь одну, например или (), то можно определить и остальные.
Сложность расчета заключается в том, что тепловые потоки и входят в подынтегральное выражение при не известном законе их изменения по высоте твэла . Решение задачи в этом случае разбивается по высоте на 
участков, в пределах которых можно считать постоянным, например нейтральный радиус . При этом расчет ведется согласно следующему алгоритму.
|
|
|
На входе первого участка 
и уравнение (83), после подстановки в него 
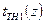и согласно (5) будет содержать только одну неизвестную - . Определив таким образом нейтральный радиус и соответственно тепловые потоки по (85), из уравнений температуры теплоносителя и 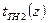в конце первого участка (в пределах участка 
), которые, в свою очередь, будут являться входными для второго участка. Далее, аналогично определяются , и , неизменные в пределах участка и выходные температуры теплоносителя. Расчет ведется до выходного сечения твэла.
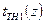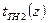Рассчитав таким образом распределение температур теплоносителя и , тепловых потоков 
и 
, далее можем найти распределение температуры оболочки 
и 
на внутренней и внешней поверхностях кольцевого твэла 
(на нейтральном радиусе), используя полученные ранее соотношения.
Кроме рассмотренной схемы, практический интерес представляет иные исполнения технологического канала, когда теплоноситель поступает сначала, например, во внутренний канал, а затем после поворота в нижней части на 1800 омывает кольцевой твэл с внешней стороны и отводится с внешнего торца (рис.5).
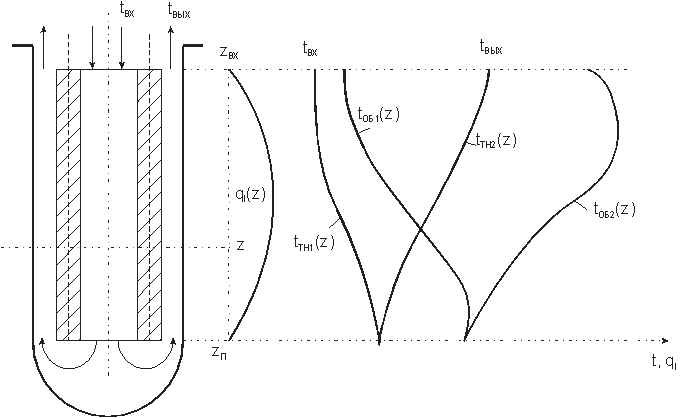
Рис. 5. Схема кольцевого твэла с двумя ходами теплоносителя.
В данном случае, как и в предыдущем, реализуется двусторонний теплоотвод с образованием нейтральной поверхности радиусом 
и тепловыми потоками во внутреннем канале и во внешнем. Коэффициенты теплоотдачи и при такой схеме однозначно определяются по известному расходу теплоносителя. Температура теплоносителя во внутреннем канале определяется выражением:
, (90)
где 
- количество тепла, затраченного на подогрев теплоносителя на участке от 
до с внутренней стороны канала.
Температура теплоносителя с внешней стороны твэла в том же сечении определяется аналогично:
, (91)
где 
- количество тепла, затраченного на подогрев теплоносителя на участке от до 
( - координата в точке поворота) с внутренней стороны от нейтрального радиуса и далее от до с внешней стороны (рис. 4.).
Вычитая из (91) (90), получим
(92)
С учетом соотношения (92), в уравнении (83), записанном для схемы с двумя ходами теплоносителя неизвестные температуры теплоносителе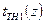й и 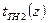исключаются и остаются при неизвестных , и , которые определяются так же, как и для схемы с одним ходом теплоносителя. Далее, по известным соотношениям находятся распределение температуры теплоносителя и оболочек твэла с внутренней и наружной сторон, а также высотное распределение максимальной температуры топлива. При этом, расчет коэффициентов теплоотдачи, как и для первой схемы, ведется по следующим формулам:
|
|
|
(93)
Здесь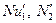 
- значение числа Нуссельта при теплообмене только через внутреннюю поверхность кольцевого канала диаметром 
и при теплообмене только через наружную поверхность кольцевого канала диаметром 
, соответственно определяется соотношениями:
, (94)
где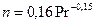 
; 
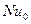- число Нуссельта для круглой трубы, определяемое формулой:
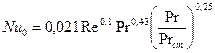(95)
Все числа Нуссельта рассчитываются по гидравлическому диаметру кольцевого канала 
. Коэффициенты 
в формулах (93) определяются выражениями:
(96)
В случае равенства тепловых потоков 
, имеем
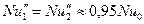(97)
Расчет ТВС с холостым ходом теплоносителя
(трубка Фильда).
Так называемые ТВС с холостым ходом теплоносителя могут применяться наряду с рассмотренной выше схемой, когда кольцевой твэл охлаждается теплоносителем при двухходовом движении. Эти схемы могут быть использованы, если необходимо, например, высвободить один торец активной зоны от подводящих коммуникаций. Схемы каналов с холостым ходом теплоносителя показаны на рис.6.
Рис.6. Схемы каналов с холостым ходом теплоносителя:
а) – теплоноситель сначала омывает твэл и выходит из канала холостым ходом ();
|
|
|
