 |
Расчет цилиндрической зубчатой передачи редуктора
|
|
|
|
Выбор электродвигателя и кинематический расчет
Общий кпд привода находим по таблице 1.1 [1,с.5]:
h=h1h2h33, (1)
где h1=0,98 – кпд зубчатой цилиндрической передачи;
h2=0,95 – кпд клиноременной передачи;
h3=0,99 – кпд пары подшипников качения.
h=0,98×0,95×0,993=0,9.
Мощность на валу барабана:
 , (2)
, (2)
где F=2,5 кН – тяговое усилие на барабане;
V=1,6 м/с – скорость ленты.

Требуемая мощность электродвигателя:
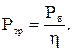 (3)
(3)
где Рб – мощность на валу барабана, кВт.

По ГОСТ 19523-81 выбираем электродвигатель 4АМ132S6У3 с синхронной частотой вращения n1=1000 мин-1, с параметрами Рдв=5,5 кВт и номинальная частота вращения nдв=965 об/мин[1, с.390].
Угловая скорость на валу электродвигателя:
 ; (4)
; (4)

Частота вращения вала барабана:
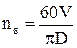 ; (5)
; (5)
где D=410 мм – диаметр барабана.

Общее передаточное отношение:
u=nдв/nб; (6)
u=965 / 74,57 = 12,94.
Принимаем передаточное число зубчатой передачи [1, с.36]:
U2=5,
тогда передаточное число клиноременной передачи:
u1 =u / u2; (7)
u1= 12,94 / 5 = 2,59.
Частота вращения:
– на валу электродвигателя:
nдв=965 мин-1;
– на ведущем валу:
n1=nдв/u1;
n1=965/ 2,59 = 372,6 мин-1;
– на ведомом валу:
n2=n1/u2;
n2=372,6 / 5 = 74,52 мин-1;
- на валу барабана:
n3=n2;
n3= 74,52 мин-1.
Угловые скорости:
на валу электродвигателя wдв=100 c-1;
на ведущем валу:
w1=wдв/u1= 100/ 2,59 = 38,61 с-1;
на ведомом валу:
w2=w1/u2;
w2=38,61 / 5 = 7,72 с-1;
на валу барабана:
w3=w2;
w3= 7,72 с-1.
Вращающие моменты:
на валу электродвигателя:
 (8)
(8)

на ведущем валу:
Т1=Тдв u1h1h4=55×2,59×0,95×0,99=133,97 Н м;
на ведомом валу:
Т2=Т1 u2h2h4;
Т2=133,97×5×0,98×0,99 =650 Н×м;
на валу барабана:
Тб=Т2 =650 Н×м.
Таблица 1
| Число оборотов, n, мин-1 | Угловая скорость, w, с-1 | Крутящий момент, Т, Н×м | |
| Вал двигателя | |||
| Ведущий вал I редуктора | 372,6 | 38,61 | 133,97 |
| Ведомый вал II редуктора | 74,52 | 7,72 | |
| Вал барабана | 74,52 | 7,72 |
|
|
|
2. Расчет клиноременной передачи
Принимаем тип ремня Б.
Диаметр меньшего шкива:
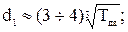 (26)
(26)

Принимаем d1=125 мм.
Диаметр большего шкива:
d2=u1d1(1-e); (27)
d2=2,59×125×(1–0,01)=320,51 мм.
Принимаем d2=315 мм.
Уточняем передаточное отношение:
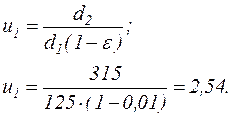
Отклонение:
d= 
что меньше допускаемого ±4%.
Окончательно принимаем диаметры шкивов d1=125 мм и d2=315 мм.
Межосевое расстояние:
amin=0,55(d1+d2)+T0; (28)
amin =0,55(125+315)+10,5=252,5 мм.
amax=d1+d2; (29)
amax=125+315=440 мм.
Принимаем aр=346 мм.
Расчетная длина ремня:
 (30)
(30)

Принимаем по ГОСТ L=1400 мм.
Уточненное значение межосевого расстояния с учетом стандартной длины ремня:
 ; (31)
; (31)

Угол обхвата меньшего шкива:
 (32)
(32)

Скорость ремня V, м/с, определяется по формуле:
 (33)
(33)
 .
.
Частота пробегов ремня U, с-1:
 (34)
(34)

Число ремней z определяется по формуле:
 (35)
(35)
где Р – мощность, передаваемая клиноременной передачей;
Р=Рдв=5,5 кВт;
Р0 – мощность, передаваемая одним клиновым ремнём [1, c.132]:
Р0=1,56 кВт;
 – коэффициент режима работы [1, c.136]: Ср=1,1.
– коэффициент режима работы [1, c.136]: Ср=1,1.
 – коэффициент, учитывающий влияние длины ремня [1, c.135]:
– коэффициент, учитывающий влияние длины ремня [1, c.135]:
С l =0,86;
 – коэффициент, учитывающий влияние угла обхвата [1, c.135]:
– коэффициент, учитывающий влияние угла обхвата [1, c.135]:
Ca=1.

Принимаем z=5.
Сила предварительного натяжения ремня F0, H,:
 (36)
(36)
где  – коэффициент, учитывающий влияние центробежных сил
– коэффициент, учитывающий влияние центробежных сил
[1,c.136]: 

Сила давления на вал FВ, Н:
 (37)
(37)

Канавки шкивов клиноременных передач по ГОСТ 20889-80 [1, с.138]:
для ремня сечения Б:
lp=14,0 мм; h=10,5 мм; h0=4,2 мм; f=12,5 мм; e=19,0 мм; a=340.
Ширина шкива В, мм:
B=(z–1)e+2f; (38)
В=(5–1)×19+2×12,5 = 101 мм.
Расчет цепной передачи
Определяем число зубьев  ведущей звездочки:
ведущей звездочки:

 (4.1)
(4.1)
Принимаем 
Определяем число зубьев 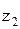 ведомой звездочки:
ведомой звездочки:
 (4.2)
(4.2)

Принимаем 
Определяем фактическое передаточное отношение 
 (4.3)
(4.3)

Определяем отклонение  от полученного ранее U:
от полученного ранее U:



Отклонение допустимо, так как не превышает 4%.
Определяем расчетный коэффициент нагрузки 
 (3.5)
(3.5)
где Кд – динамический коэффициент, Кд=1;
|
|
|
Ка – коэффициент, учитывающий влияние межосевого расстояния, Ка=1;
Кн – коэффициент, учитывающий влияние наклона цепи, Кн=1;
Кр – коэффициент, учитывающий способ регулировки натяжения цепи, Кр=1,25;
Ксм – коэффициент, учитывающий способ смазывания цепи, Ксм=1,4;
Кп – коэффициент, учитывающий периодичность работы передачи, Кп=1.
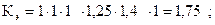
Определяем шаг цепи t, мм:
t= 2,8 
 ; (3.6)
; (3.6)
 ; (3.7)
; (3.7)

t= 2,8 
По ГОСТу 13568-75 принимаем большее ближайшее значение t=31,75 мм.
Выбираем цепь ПР-25,4-60 ГОСТ 13568-75,имеющую:
Шаг цепи t=31,75 мм;
Разрушающую нагрузку Q=88,5 кН;
Массу одного метра цепи q=3,8 кг/м
Проекцию опорной поверхности шарнира Аоп=262 мм2.
Проверяем цепь с шагом t=31,75 мм по частоте вращения: допускаемая для цепи частота вращения,  следовательно, условие
следовательно, условие  выполнено, так как 96,5 < 800 об/мин.
выполнено, так как 96,5 < 800 об/мин.
Определяем расчетное давление p, МПа:
 (3.8)
(3.8)
где 
 – окружная сила, передаваемая цепью, Н;
– окружная сила, передаваемая цепью, Н;
 , (3.9)
, (3.9)
где V – фактическая скорость цепи, м/с.
 (3.10)
(3.10)
 м/с.
м/с.
 =3178 Н.
=3178 Н.

Условие нагружения цепи 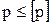 выполнено:
выполнено:

Из условия долговечности цепи оптимальное межосевое расстояние в шагах  должно находиться в пределах:
должно находиться в пределах:  =а/t=30…50.
=а/t=30…50.
Принимаем  =40.
=40.
Определяем число звеньев цепи  по формуле:
по формуле:
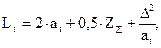 (3.11)
(3.11)
где  – суммарное число зубьев:
– суммарное число зубьев:
 (3.12)
(3.12)

 (3.13)
(3.13)

Округляем до четного числа 
Уточняем межосевое расстояние а, мм:
 (3.14)
(3.14)
 1252 мм.
1252 мм.
Определяем диаметры делительных окружностей  , мм, звездочек:
, мм, звездочек:
 (3.15)
(3.15)
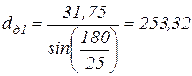 мм.
мм.
 677,37 мм.
677,37 мм.
Определяем диаметры наружных окружностей звездочек:
 (3.16)
(3.16)
где  – диаметр ролика цепи,
– диаметр ролика цепи,  =15,88 мм;
=15,88 мм;
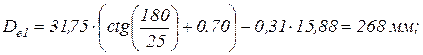
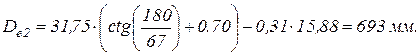
Определяем центробежную силу 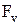 ,Н:
,Н:
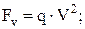 (3.17)
(3.17)

Определяем предварительное натяжение цепи от провисания ведомой ветви:
 , (3.18)
, (3.18)
 Н.
Н.
Определяем силу давления цепи на вал 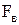 ,Н:
,Н:
 ; (3.19)
; (3.19)
 Н.
Н.
Определяем расчетный коэффициент запаса прочности S:
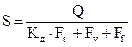 ; (3.20)
; (3.20)
 =23,8.
=23,8.
Прочность цепи удовлетворяется соотношением 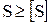 ,
,
где  – допускаемый коэффициент запаса прочности для роликовых (втулочных) цепей.
– допускаемый коэффициент запаса прочности для роликовых (втулочных) цепей.  =7,6.
=7,6.
23,8>7,8.
Условие прочности выполнено.
Расчет цилиндрической зубчатой передачи редуктора
Выбираем материалы: для шестерни сталь 40Х, термическая обработка – улучшение, 260 НВ, для зубчатого колеса сталь 40Х, термическая обработка – улучшение, 240 НВ.
Предел контактной выносливости [1, с.34, т.3.2]:
для шестерни
sHlimb1=2HB1+70=2×260+70=590 МПа;
|
|
|
для зубчатого колеса
sHlimb2=2HB2+70=2×240+70=550 МПа.
Допускаемые контактные напряжения:
для шестерни
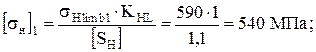
для зубчатого колеса

где KHL=1 – коэффициент долговечности [1, с.33],
[SH]=1,1 – коэффициент безопасности [1, с.33].
Расчетное допускаемое контактное напряжение:
[sH]=0,45([sH1]+[sH2])=0,45×(540+500)=466 МПа. (9)
Требуемое условие [sH]<1,23[sH]2=615 МПа выполнено.
Принимаем значение коэффициентов: [1, с.32]
KHB=1,25; Ka=43; yba=0,4.
Определяем межосевое расстояние из условия контактной выносливости зубьев:
 ; (10)
; (10)
где Т2=650 Н м – крутящий момент на ведомом валу;

Ближайшее значение межосевого расстояния по ГОСТ 2185-66 [1, с.36]:
aw=180 мм.
Нормальный модуль зацепления:
mn=(0,01-0,02)aw; (11)
mn =(0,01-0,02)×180=1,8¸3,6 мм.
Принимаем модуль по ГОСТ 9563-60 [1, с.36]:
mn=2,5 мм.
Примем предварительно угол наклона зубьев [1, с.36]:
b=100.
Определяем число зубьев:
шестерни
 (12)
(12)

Принимаем z1=23,
тогда число зубьев зубчатого колеса
z2=z1 u1;
z2=23×5=115.
Уточненное значение угла наклона зубьев:
 ;
;
 .
.
Откуда, b=16,60.
Делительные диаметры:
шестерни
 (13)
(13)
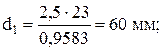
зубчатого колеса
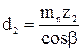 ;
;

Уточняем межосевое расстояние:


Диаметры вершин:
шестерни
da1=d1+2mn;
da1=60+2×2,5=65 мм;
колеса
da2=d2+2mn;
da2=300+2×2,5=305 мм.
Ширина колеса:
b2=ybaaw; (14)
где yba=0,4 – коэффициент ширины венца;
b2=0,4×180=72 мм.
Ширина шестерни:
b1=b2+5;
b1=72+5=77 мм.
Определяем коэффициент ширины шестерни по диаметру:
ybd=  ; (15)
; (15)
 .
.
Окружная скорость колес:
 (16)
(16)

При такой скорости для косозубых колес по ГОСТ 1643-81 принимаем 9-ю степень точности.
Принимаем значения коэффициентов: [1, с.39-40]:
KHb=1,04; KHV=1; KНa=1,08.
Определяем коэффициент нагрузки:
KH=KHbKHVKHa;
КН=1,04×1×1,08=1,1232.
Проверяем контактные напряжения:
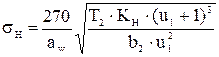 ; (17)
; (17)

Условие sH<[sH] выполнено: 444 < 466 МПа, следовательно, считаем, что контактная прочность передачи обеспечена.
Силы, действующие в зацеплении:
окружная
Ft= 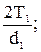 (18)
(18)
Ft 
Радиальная
 (19)
(19)
Fr 
Осевая
Fa=Fttgb; (20)
Fa=3555×0,2981 =1059 H.
Значение предела выносливости при нулевом цикле изгиба:
для шестерни
sFlimb1=1,8HB1;
sFlimb1=1,8×260=468 МПа;
для колеса
sFlimb2=1,8HB2;
sFlimb2=1,8×240=432 МПа.
Коэффициент безопасности:
[SF]=[SF]' [SF]'';
где [SF]'=1,75; [SF]''=1 [1, c.44];
|
|
|
[SF]=1,75×1=1,75.
Допускаемые напряжения:
для шестерни
 ; (21)
; (21)

для колеса
 ; (22)
; (22)
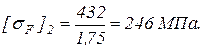
Эквивалентное число зубьев:
шестерни
 (23)
(23)
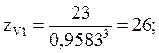
колеса
 (24)
(24)

Коэффициент, учитывающий форму зуба [1, с.42]:
YF1=3,8; YF2=3,6.
Находим отношение:

Дальнейший расчет ведем для зубьев колеса, для которого найденное отношение меньше.
Коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба [1, c.43]:
KFb=1,10.
Коэффициент, учитывающий динамическое действие нагрузки [1, c.43]:
KFV=1,3.
Коэффициент нагрузки:
KF=KFbKFV;
КF=1,1×1,3=1,43.
Определяем коэффициенты:
Yb=1–b/1400;
Yb=1–16,60/1400=0,88;
KFa=0,92.
Проверяем зубья на выносливость по напряжениям изгиба:
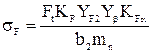 ; (25)
; (25)

Условие sF<[sF]2 выполнено, 84<246 МПа.
|
|
|


