 |
Описание метода и установки
|
|
|
|
ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Цель работы. Построение эквипотенциальных линий электростатического поля с помощью экспериментального моделирования в проводящей среде, в которой протекает переменный ток.
Электростатическое поле
Если в пространстве имеется система заряженных тел, то в каждой точке этого пространства существует силовое электростатическое поле, которое определяется силой, действующей на «пробный» заряд в данной точке пространства. «Пробный» заряд qо должен быть точечным и достаточно малым, чтобы не вносить существенных искажений в силовое поле, созданное системой зарядов. Чтобы силовая характеристика электростатического поля не зависела от величины «пробного» заряда, силу, действующую на «пробный» заряд, относят к величине этого заряда:
.
Силовое электростатическое поле можно представить графически в виде силовых линий, называемых линиями напряженности. Вектор напряженности 
в каждой точке такой линии, направлен по касательной к ней и совпадает с ней по направлению. Густота линий характеризует величину напряженности электростатического поля. Вблизи зарядов эти линии сгущаются, и напряженность возрастает. Направление электростатического поля совпадает с направлением силы, действующей на положительный заряд в данной точке пространства. Силовые линии начинаются на положительных и заканчиваются на отрицательных зарядах или уходят на бесконечность. Силовые линии электростатического поля незамкнуты. Сила, действующая на точечный заряд величиной q, полностью определяется величиной самого заряда и напряженностью электростатического поля в данной точке пространства
|
|
|
.
Основное свойство электростатического поля выражается принципом суперпозиции - напряженность поля, созданного несколькими зарядами, равна векторной сумме напряженностей, создаваемых каждым из зарядов в отдельности
.
Так как силы взаимодействия двух точечных зарядов направлены вдоль линии их соединяющих и зависят лишь от расстояния между ними, то сила, действующая на заряд, помещенный в электростатическое поле, является центральной и, следовательно, консервативной. Вследствие этого работа по перемещению заряда в электростатическом поле не зависит от траектории движения, а определяется лишь начальным и конечным положениями заряда. Поэтому электростатическое поле является потенциальным ввиду физической природы сил, действующих между зарядами.
В каждой точке пространства можно ввести энергетическую характеристику электростатического поля - потенциал j. При перемещении «пробного» заряда q 0 из точки 1 с потенциалом j 1 в точку 2 с потенциалом j 2 по произвольному пути силами электростатического поля совершается работа
.
Следовательно, разность потенциалов между точками 1 и 2 (j 1 - j 2)можно определить как отношение работы сил поля А 12 к величине заряда q o:
.
При бесконечно малом перемещении 
заряда в произвольном направлении силой поля совершается работа 
, где 
, с другой стороны, 
. Тогда 
и, таким образом, установлена связь между силовой характеристикой и энергетической характеристикой j электрического поля.
Выразим из последнего выражения величину . Для этого запишем векторы и через их проекции на оси декартовой системы координат:
;
,
где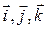 
- орты осей 
соответственно.
По правилу скалярного произведения векторов получим
.
Дифференциал функции координат j равен
.
Учитывая, что , из двух последних выражений, сравнивая их, получаем
.
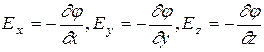Следовательно, для вектора можно записать
,
т.е. вектор напряженности электростатического поля равен градиенту его потенциала со знаком минус. Вводя оператор набла
|
|
|
,
эту же связь можно записать, используя этот оператор, в виде
.
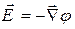Итак, силовая и энергетическая характеристики электростатического поля связаны друг с другом.
Поверхности равного потенциала j = const называются эквипотенциальными. Из соотношения следует, что при перемещении заряда вдоль эквипотенциальной поверхности работа электростатического поля равна нулю, что возможно только в случае, когда вектор напряженности перпендикулярен к этой поверхности. Поскольку вектор направлен вдоль касательной к силовой линии, это означает, что силовые линии пересекают эквипотенциальные поверхности под прямым углом.
Метод измерений
В слабо проводящую среду, которую представляет собой недистиллированная вода, помещают два металлических проводника, подсоединенных к источнику переменного тока. Так как проводимость среды намного меньше проводимости помещенных в нее металлических электродов, то потенциал в разных точках этих электродов с достаточной степенью точности можно считать одинаковым. При этом топография поля в пространстве между ними будет такой же, какой была бы топография электростатического поля между заряженными проводниками, помещенными в однородную непроводящую среду.
В однородной изотропной среде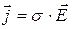 
, здесь 
- вектор плотности тока в проводящей среде, s - удельная электропроводность (проводимость) среды.
Метод моделирования электростатического поля в проводящей среде основан на аналогии уравнений, описывающих электрическое поле в вакууме и в изотропной проводящей среде. Метод является удобным для практики, так как позволяет получить путем экспериментального моделирования сложную картину электростатического поля, аналитический расчет которого зачастую невозможен из-за сложности граничных условий. Использование переменного тока позволяет предотвратить выделение на электродах составных частей электролита. Для переменного синусоидального тока в электролите переменное электрическое поле не является потенциальным, в каждой точке напряжение изменяется со временем. Однако понятие «эквипотенциальной поверхности» как поверхности постоянно изменяющегося, но одинакового по амплитуде потенциала можно считать справедливым. Разные эквипотенциальные поверхности при этом характеризуются разным значением амплитуды напряжения.
|
|
|
Измерительная установка
Измерительная установка (см. рисунок) включает в себя электролитическую ванну 1, заполненную водой, два электрода 2 и 3, выполненные в виде пластин или тел другой геометрической формы, подсоединенные к источнику переменного напряжения 4 (~ 6В), зонд 5, погруженный своим концом в электролит, вольтметр 6, регистрирующий напряжение между электродом 2 и зондом 5, а также проводящее тело (например, металлическое кольцо), предназначенное для погружения в электролит с целью создания в нем неоднородного электрического поля (на рис. не показано).
На дне электролитической ванны имеется координатная сетка, позволяющая воспроизвести картину поля в определенном масштабе на чертежах. Зонд 5 устанавливается вертикально на одну из линий сетки, его координаты отмечаются на чертеже. Зонд 5 перемещается между электродами до тех пор, пока ни будут найдены ~10 таких точек, для которых разность потенциалов между электродом 2 и зондом 5 равна некоторому постоянному значению. Координата зонда 5 для каждой из десяти точек отмечается на чертеже. Геометрическое место этих точек дает одну эквипотенциальную поверхность. Потенциал данной эквипотенциальной поверхности измеряется относительно электрода 2. Построив несколько эквипотенциальных поверхностей с одинаковой разностью потенциалов между ними, получим картину поля между электродами. Разность потенциалов между двумя эквипотенциальными поверхностями и известное расстояние между ними позволяют, как показано выше, оценить величину напряженности электрического поля.
Порядок выполнения работы
1. Согласуйте с преподавателем конфигурацию исследуемого поля.
2. Соберите схему согласно рисунку.
3. Начертите в определенном масштабе координатную сетку и отметьте на ней положение и форму электродов.
|
|
|
4. Подключите электроды к источнику переменного напряжения ~ 6В.
5. С помощью вольтметра найдите точки, равноотстоящие по потенциалу (эквипотенциальные поверхности принято проводить так, чтобы между любыми соседними эквипотенциальными поверхностями разность потенциалов была бы одна и та же). Таких точек (число эквипотенциальных линий) нужно наметить в пространстве между электродами семь-восемь.
6. Постройте эквипотенциальные линии для каждой из намеченных точек. Каждую линию следует проводить не менее чем по 10 точкам. Зонд при измерениях держите вертикально.
7. По полученной картине эквипотенциальных линий проведите 6-7 силовых линий. Оцените величину Е - напряженности электрического поля.
8. Положите в ванну проводящее тело (по указанию преподавателя, например, кольцо).
9. Начертите картину поля, повторив п.5-7.
Контрольные вопросы
1. В чем заключается цель настоящей работы?
2. Как найти точки с одинаковым значением потенциала?
3. Как определить значение потенциала на эквипотенциальной поверхности, относительно какого тела он определяерся?
4. Что такое напряженность и потенциал электростатического поля?
5. Какова связь напряженности с разностью потенциалов?
6. Каково взаимное влияние проводящего тела и электростатического поля?
7. Каково взаимное влияние диэлектрического тела и электростатического поля?
8. Сформулируйте теорему Гаусса для вектора напряженности электростатического поля в вакууме. Объясните, для чего и как она применяется.
Список литературы
1. Калашников С.Г. Электричество.- М.: Наука, 1974
2. Савельев И.В. Курс общей физики. - М.: Наука, 1982.- Т.2 и последующие издания этого курса.
3. Барановский С.Н., Березиков Д.Д., Погорельский А.М., Потапов Н.П., Юровская С.М. Механика. Электричество. Магнетизм.- Новосибирск, 1995
Лабораторная работа № 11
ИЗУЧЕНИЕ РАБОТЫ цепи
Цель работы. Проверить теоретическую зависимость полной, полезной мощности, мощности потерь, падения напряжения во внешней цепи и КПД батареи от силы тока с помощью метода «холостого хода и короткого замыкания».
Описание метода и установки
|
Электрическая схема измерительной установки (рис.1) состоит из внешнего сопротивлений R источника постоянного напряжения с электродвижущей силой e [1, с.146-147, 149-152; 2, с. 97-99] и внутренним сопротивлением r. В схему включены амперметр и вольтметр, позволяющие измерять ток и падение напряжения во внешней цепи.
Из закона Ома для этой замкнутой цепи можно записать выражение [1, с. 151-154; с. 101-103].
e= IR + Ir, (1)
где I - сила тока в цепи;
|
|
|
U = IR - напряжение на сопротивлении R.
Умножив обе части уравнения (1) на силу тока, протекающего по цепи, получим
Ie = I2R + I2r. (2)
Уравнение (2) представим в виде
P = P 1 + P 2 (3)
где P = Ie - полная мощность, развиваемая батареей;
P 1 = I2R = IU - полезная мощность, т.е. мощность, развиваемая батареей во внешней цепи (на сопротивлении R);
P 2 = I2r - потери мощности внутри батареи (на сопротивлении r).
Установим зависимость мощностей [1, с.163-165; с. 105-106] от силы тока.
Графически (рис.2) зависимость P от I выражается прямой линией, проходящей через начало координат.
| Полезная мощность из (2) может быть представлена в виде
P 1 = e×I - I2×r (4)
Эта зависимость выражается параболой. Найдем значение тока, при котором полезная мощность максимальна. Для этого, взяв первую производную 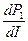 , приравняем ее нулю
|
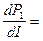e - 2Ir, (5)
откуда, при 
, получим
I m = 
(6)
Так как вторая производная 
отрицательна, то при значении силы тока I m мощность P 1 имеет максимальную величину
P 1max = 
.
Сравнивая по току выражения (6) и получаемое из (1), увидим, что при 
выполняется равенство 2r = R+r или R = r. Следовательно, полезная мощность P 1 максимальна при условии, что сопротивление нагрузки равно внутреннему сопротивлению источника питания R = r.
Потери мощности определяются зависимостью
P 2 = I2r (7)
Графически зависимость P 2 от I - парабола с вершиной в начале координат, а ее ветвь направлена вверх (рис.2).
(8)
Представим выражение для U из (1) в (8)
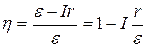(9)
Из уравнения (9) видно, что зависимость h от I выражается прямой линией, убывающей от значения h = 1 при I = 0 до h = 0 при
I k = 
. (10)
Это значение тока - ток «короткого замыкания» [1, с.154]. Действительно, из (1) видно, что при внешнем сопротивлении R = 0 («короткое замыкание» цепи) сила тока достигает наибольшего значения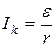 
. Полезная мощность P 1 при этом убывает до нуля (рис.2), так как при R = 0
.
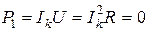Полная мощность P = e×Ik и потери мощности 
при I = Ik достигают наибольшего значения и равны друг другу
P max = P 2max = 
.
Найдем значение КПД и соотношения между мощностями P, P 1, P 2 при максимуме мощности P 1 = P 1max. Так как полезная мощность максимальна при условии, что R = r, то
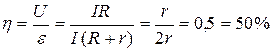(11)
Отсюда, при I = I m, P 1max = 0,5P. Используя (3), получим, при I = I m, P 1max = P 2.
Из графиков зависимостей мощностей и КПД от силы тока (рис.2) видим, что условия получения наибольшей полезной мощности P 1max и наибольшего КПД hmax несовместимы. Когда P 1 достигает наибольшего значения, сила тока равна I m и h = 0,5 или 50%. Когда же КПД близок к единице, полезная мощность P 1 мала по сравнению с максимальной мощностью P 1ma x , которую мог бы развить данный источник.
Выразив напряжение U = e - Ir, построим зависимость U = f(I) (рис.2). Это - прямая, спадающая от значения U Х (напряжение «холостого хода»), равного U Х = e, до нуля при токе равном току «короткого замыкания». Графический метод определения тока «короткого замыкания» I К и ЭДС e = U Х, так называемый метод «короткого замыкания и холостого хода» является простым и единственным методом, позволяющим, не измеряя, определить I К и e..
На практике он используется следующим образом. Изменяя в некоторых пределах сопротивление R, измеряют ток I и напряжение U. На чертеже строят зависимость U = f(I), графиком которой будет прямая линия. Продолжив ее до пересечения с осью напряжения U, находят значение U Х = e, а до пересечения с осью тока I, находят ток I К. Внутреннее сопротивление источника ЭДС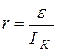 
.
Задание к работе
1. Предварительно подготовьте протокол, в котором начертите таблицу для прямых и косвенных измерений.
2. Постройте на миллиметровой бумаге необходимые оси координат.
3. Соберите электрическую схему установки. В качестве источника с электродвижущей силой e и внутренним сопротивлением r используйте генератор постоянного напряжения ГПН с включенным тумблером «внутреннее сопротивление» R ВН на его передней панели.
4. Изменяя сопротивление R цепи, снимите зависимость U от I и постройте ее график. Определите по графику путем его экстраполяции до пересечения с осями координат значения ЭДС и тока «короткого замыкания» I К.
5. Определите по формуле (10) внутреннее сопротивление r источника тока.
6. Вычислите значения P, P 1, P 2, h.
7. Постройте зависимости этих величин от тока, экстраполируя кривые и прямые до пересечения с осями координат.
Вопросы к защите
1. Закон Ома для замкнутой цепи. Физический смысл ЭДС.
2. Каким должно быть сопротивление вольтметра, чтобы измеренное им значение ЭДС совпало с истинным?
3. Дайте определение полной, полезной мощности и мощности потерь.
4. При каком условии полезная мощность будет максимальна? Докажите.
5. Проанализируйте зависимости мощностей P, P 1, P 2 от силы тока.
6. Коэффициент полезного действия батареи. Проанализируйте зависимость h = f(I).
7. Сравните полученные опытным путем зависимости с теоретическими.
8. Физический смысл напряжения, разности потенциалов.
Список литературы
1. Калашников С.Г. Электричество. - М.: Наука, 1964
2. Савельев И.В. Курс общей физики. - М.: Наука, т. 2, 1978 и последующие издания этого курса.
Лабораторная работа № 12
|
|
|
