 |
Свойства параллельного проектирования.
|
|
|
|
Движение и равенство фигур.
Из различных преобразований фигур самыми важными являются такие, при которых сохраняются все их свойства; расстояние между точками, углы, параллельность отрезков, площади и т.д. Оказывается, что для этого достаточно потребовать только сохранения расстояния между точками данной фигуры. Тогда у фигуры, которая получается при преобразовании, сохраняются и все остальные геометрические свойства, так как они зависят от расстояний.
Определение. Преобразование фигуры F в фигуру F', которое сохраняет расстояние между точками, называется движением фигуры F.
Движение сопоставляет любым точкам А и В фигуры Этакие точки А' и В' фигуры F', что АВ = А'В'. В геометрии доказано, что преобразования симметрии относительно точки и прямой, являются движениями. Кроме того, движениями являются параллельный перенос фигуры, поворот фигуры вокруг точки на данный угол.
Движения фигур обладают рядом свойств, некоторые из которых мы сформулируем, не доказывая.
1. При движении точки, лежащие на прямой, переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.
2. Отрезок движением переводится в отрезок, луч переходит в луч, прямая - в прямую.
3. Треугольник движением переводится в треугольник.
4. Движение сохраняет величины углов.
5. Преобразование, обратное движению, также является движением. В геометрии движения играют важную роль. Изменяя расположение фигур на плоскости, они не меняют ни их размеры, ни их формы. С точки зрения геометра, фигуры, отличающиеся лишь своим положением на плоскости, совершенно одинаковы, именно поэтому они называются равными (или конгруэнтными). Ни одно свойство геометрической фигуры не отличается от соответствующего свойства равной ей фигуры. Например, равные треугольники имеют не только соответственно равные стороны и углы, но и соответственно равные медианы, высоты, площади и т.д.
|
|
|
Определение. Фигура F равна фигуре F', если фигуру F' можно получить некоторым движением фигуры F.
Используя понятие взаимно однозначного соответствия, это определение можно сформулировать так: фигуры F и F' называются равными, если между их точками существует такое взаимно однозначное соответствие, что отрезки, соединяющие соответственные точки, равны.
Устанавливая равенство отрезков, углов, треугольников и других фигур, нет необходимости преобразовывать одну фигуру в другую. Достаточно сравнить те размеры фигур, которыеих однозначно определяют. Например, у треугольников сравнить расстояния между вершинами, т.е. длины сторон.
Когда же рассматривают произвольные фигуры, необходимо определение их равенства через движение.
Нетрудно убедиться в том, что равенство фигур рефлексивно, симметрично и транзитивно, т.е. является отношением эквивалентности. Поэтому это отношение порождает на множестве геометрических фигур классы эквивалентности, содержащие равные между собой фигуры. С позиций геометрии такие фигуры неразличимы и их можно принять за одну и ту же фигуру. Именно поэтому можно сказать, что задача построения прямоугольника по двум сторонам а и b имеет только одно решение.
Сказанное позволяет уточнить наше понимание предмета геометрии - она изучает свойства фигур, не зависящие от их расположения. Или, другими словами, геометрия изучает те свойства фигур, которые сохраняются при движениях.
Свойства параллельного проектирования.
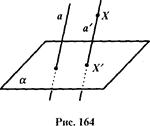
Пусть даны плоскость α и пересекающая ее прямая а. Возьмем в пространстве произвольную точку X, не принадлежащую прямой а и проведем через Х прямую а ', параллельную прямой а (рис.). Прямая а' пересекает плоскость в некоторой точке X'', которая называется параллельной проекцией точки Х на плоскость а.
|
|
|
Если точка Х лежит на прямой а, то ее параллельной проекцией X' является точка, в которой прямая а пересекает плоскость α.
Если точка Х принадлежит плоскости а, то точка X' совпадает с точкой X.
Таким образом, если заданы плоскость α и пересекающая ее прямая а, то каждой точке Х пространства можно поставить в соответствие единственную точку X' - параллельную проекцию точки Х на плоскость α (при проектировании параллельно прямой а). Плоскость α называется плоскостью проекций. О прямой а говорят, что она задает направление проектирования - при замене прямой а любой другой параллельной ей прямой результат проектирования не изменится. Все прямые, параллельные прямой а, задают одно и то же направление проектирования и называются вместе с прямой а проектирующими прямыми.
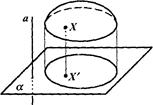
Проекцией фигуры F называется множество F проекцией всех ее точек. Отображение, сопоставляющее каждой точке Х фигуры F ее параллельную проекцию - точку X' фигуры F, называется параллельным проектированием фигуры F (рис.).
Параллельной проекцией реального предмета является его тень, падающая на плоскую поверхность, при солнечном освещении, поскольку солнечные лучи можно считать параллельными.
Параллельное проектирование обладает рядом свойств, знание которых необходимо при изображении геометрических тел на плоскости. Сформулируем основные, опустив их доказательство.
Теорема. При параллельном проектировании для прямых, не параллельных направлению проектирования, и для лежащих на них отрезков выполняются следующие свойства:
1. Проекция прямой есть прямая, а проекция отрезка - отрезок.
2. Проекции параллельных прямых параллельны или совпадают.
3. Отношение длин проекций отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин самих отрезков.
Из этой теоремы вытекает следствие: при параллельном проектировании середина отрезка проектируется в середину его проекции.
При изображении геометрических тел на плоскости необходимо следить за тем, чтобы указанные свойства выполнялись. В остальном оно может быть произвольным. Так, углы и отношения длин непараллельных отрезков могут изменяться произвольно, т.е., например, треугольник при параллельном проектировании изображается произвольным треугольником. Но если треугольник равносторонний, то на проекции его медиана должна соединять вершину треугольника с серединой противоположной стороны.
|
|
|
И еще одно требование необходимо соблюдать при изображении пространственных тел на плоскости - это способствовать созданию верного представления о них.
|
|
|


