 |
Разложение функций в ряд Маклорена
|
|
|
|
Числовой ряд и его сходимость. Необходимое условие
Сходимости ряда
Числовым рядом называется выражение вида
,
uk=f (k) называется общим членом ряда.
Сумма конечного числа n первых членов ряда называется п-ой частичной суммой ряда:
.
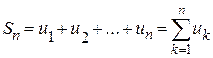Ряд un+1+un+2+…= 
называется п-м остатком ряда 
.
Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм: 
. Число S называется суммой ряда. При этом пишут = S. Если предел частичных сумм равен бесконечности, т.е. 
, или не существует, то ряд называется расходящимся.
Рассмотрим ряд из членов геометрической прогрессии (геометрический ряд):
a+aq+aq2+…+aqn+… 
a·qn.
Сумма первых п членов геометрической прогрессии вычисляется по формуле Sn=a+aq+aq2+…+aqn-1= 
, если 
. Если 
<1, то 
, т.е. ряд сходится и его сумма S= 
aqп= . Если >1,то ряд расходится: 
в случае 
и не существует в случае 
.
Итак, геометрический ряд 
aqn сходится тогда и только тогда, когда <1, и его сумма S = .
Если ряд 
сходится, то его п-й член при 
является бесконечно малой величиной, т.е.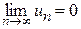 
. Это необходимое условие сходимости ряда. Если же 
, то ряд расходится (достаточный признак расходимости ряда).
Положительные ряды
Числовой ряд 
называют положительным, если все члены ряда неотрицательны, т.е. 
при любом n.
Теорема (критерий сходимости положительного ряда). Для того чтобы положительный числовой ряд сходился, необходимо и достаточно, чтобы его п-я частичная сумма была ограничена сверху, т.е. S n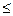 
M.
Для исследования сходимости применяют достаточные признаки. Среди них часто используют признаки сравнения, Даламбера, радикальный и интегральный признаки Коши.
Признаки сравнения
Теорема (1-й признак сравнения). Пусть даны два положительных ряда: и 
и пусть для всех п начиная с некоторого номера, выполняется 
. Тогда
|
|
|
1) если ряд сходится, то ряд также сходится;
2) если ряд расходится, то ряд также расходится.
Теорема (2-й признак сравнения). Если существует конечный, отличный от нуля предел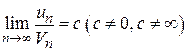 
, то ряды эквивалентны в смысле сходимости, т.е. оба ряда сходятся или расходятся одновременно.
Для сравнения используются эталонные ряды:
a) геометрический ряд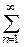 
aqп, который сходится при <1 и расходится при 
1;
б) обобщенный гармонический ряд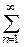 
, который сходится при р >1 и расходится при р 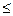1. В случае р =1 ряд называют гармоническим.
При выборе рядов для сравнения полезно помнить следующие специальные пределы:
; 
; 
;
; 
.
Удобно также использовать неравенства:
1) 
< 
< 
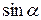, если 0< < 
;
2) 
; 
;
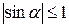3) 
< 
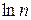для всех натуральных п и 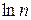>1 при 
.
Признак Даламбера. Пусть для положительного ряда 
существует конечный предел D = 
. Тогда, если D <1, то ряд сходится, если D >1 – ряд расходится, при D =1 – ничего определенного о сходимости или расходимости ряда утверждать нельзя.
Признак Даламбера используется, если в записи п- го члена ряда присутствует либо ап наряду с 
, либо факториал п!.
(читается «эн-факториал»).
Радикальный признак Коши. Пусть для положительного ряда существует конечный предел К = 
. Тогда, если К <1, торяд сходится, если К >1 – ряд расходится; при К =1 – ничего определенного о сходимости или расходимости ряда утверждать нельзя, нужно применить другой признак.
Пример 1. И сследовать на сходимость ряды:
а) 
; б) 
; в) 
; г) 
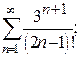д) 
Решение.
а) Для сравнения возьмем ряд 
, который сходится как обобщенный гармонический ряд (р =2>1).
Поскольку 
при п > 1, то по первому признаку сравнения исходный ряд также сходится.
б) Для сравнения возьмем ряд 
, который расходится как обобщенный гармонический ряд (р = 
<1).
Применим 2-й признак сравнения:
= 
Следовательно, ряды эквивалентны в смысле сходимости, и значит, исходный ряд также расходится.
|
|
|
в) Для сравнения возьмем ряд 
, который расходится как геометрический ряд (q = 
>1).
Поскольку un = 
> 
для всех п, то по первому признаку сравнения исходный ряд также расходится.
г) Применим признак Даламбера. Общий член ряда 
, (п +1)-й член ряда 
Вычисляя предел D =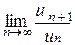 
, получаем:
D =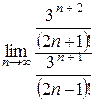 
= 
=3 
Согласно признаку Даламбера ряд сходится.
д) Используем радикальный признак Коши. Общий член ряда 
. Найдем К = 
:
К = 
= 
= 
=
= 
= 
.
Следовательно, исследуемый ряд сходится.
Замечание. При решении использован второй замечательный предел 
Знакопеременные ряды
Если члены ряда 
имеют разные знаки, то такие ряды называют знакопеременными.
Ряд 
называется абсолютно сходящимся, если сходится ряд 
,
составленный из абсолютных величин членов ряда. Ряд называется условно сходящимся, если он сходится, а ряд, составленный из абсолютных величин членов ряда 
, расходится.
Теорема. Если сходится ряд 
, составленный из абсолютных величин членов данного ряда 
, то сходится и данный ряд.
Числовые ряды, любые два соседних члена u n и u n+1 (n =1,2,…) которых имеют противоположные знаки, называются знакочередующимися.
Признак Лейбница. Пусть члены знакочередующегося ряда 
, (un 0) таковы, что
1) ,
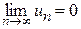2) un un +1 для всех n, т.е. члены ряда из абсолютных величин монотонно убывают, тогда ряд сходится и для любого n =1,2,… выполняется неравенство 
, где Sn – n-я частичная сумма, а S – сумма ряда .
Алгоритм исследования знакочередующихся рядов 
1) Проверить выполнено ли необходимое условие сходимости ряда: если , то ряд расходится, и исследование закончено.
2) Проверить ряд на абсолютную сходимость: если ряд 
сходится, то исследуемый ряд сходится абсолютно.
3) Если ряд не сходится абсолютно, то для исследования сходимости знакочередующегося ряда используют признак Лейбница. Если оба условия этого признака выполнены, то заключаем, что исследуемый ряд сходится условно.
Пример 2. Исследовать знакочередующиеся ряды на абсолютную и условную сходимость:
а)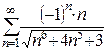 
; б) 
; в)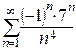 
Решение.
а) Рассмотрим ряд из абсолютных величин членов данного ряда: 
= 
= 
.
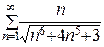Общий член этого ряда 
.
Для сравнения возьмем ряд 
, который сходится как обобщенный гармонический ряд с показателем р= 2>1.
|
|
|
Вычисляя 
, получим
= 
Следовательно, согласно второму признаку сравнения, ряд 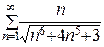тоже сходится.
Поскольку ряд, составленный из абсолютных величин членов исследуемого ряда, сходится, то исходный ряд сходится абсолютно.
б) Составляем ряд из абсолютных величин: 
и исследуем его на сходимость, выбирая для сравнения гармонический ряд 
, который расходится.
Поскольку 
при , то по первому признаку сравнения ряд также расходится. Это означает, что исследуемый знакочередующийся ряд не сходится абсолютно.
Переходим к исследованию на условную сходимость по признаку Лейбница:
1) 
.
(При раскрытии неопределенности типа 
использовали правило Лопиталя).
2) Проверим условие монотонного убывания членов ряда при возрастании номера п. Для этого рассмотрим функцию f (x)=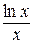 
, определенную при x >0. Ее производная 
при 
=2,718…, значит f (x) монотонно убывает при , в частности, при выполняется 
, следовательно, 
.
Итак, оба условия признака Лейбница выполнены. Значит, исследуемый ряд сходится (условно).
в) Замечая, что необходимое условие сходимости ряда не выполняется
, заключаем, что данный ряд расходится.
= 
.
Степенные ряды
Степенным рядом называется выражение вида:
где х – независимая переменная; an, n =0,1,2,…, (коэффициенты ряда) – постоянные. При всяком фиксированном числовом значении х степенной ряд превращается в числовой, который либо сходится, либо расходится. Основная задача исследования степенного ряда – нахождение его области сходимости.
Областью сходимости степенного ряда называется множество всех значений х, для которых этот ряд сходится.
Число R >0 называется радиусом сходимости степенного ряда, если ряд сходится для всех х таких, что 
, и расходится для всех х таких, что 
.
Областью сходимости степенного ряда с переменной х является интервал (- R; R), возможно, дополненный одной или обеими концевыми точками.
Если ряд сходится лишь при х =0, считают R =0; если ряд сходится при любом х, то считают R =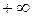 
.
Радиус сходимости степенного ряда вычисляется по одной из формул:
|
|
|
или 
.
Если имеется степенной ряд по степеням 
, т.е. ряд вида 
, то интервал сходимости ряда радиуса R имеет вид 
На концах интервала сходимости различные степенные ряды ведут себя по-разному, поэтому в этих точках требуются дополнительные исследования на сходимость для каждого конкретного ряда.
Алгоритм нахождения области сходимости степенного ряда.
1) Выписать коэффициент степенного ряда аn и в зависимости от его вида вычислить радиус сходимости ряда R.
2) Если R =0, то степенной ряд сходится лишь в одной точке х =0 (или х=х 0); если R = 
, то ряд сходится на всей числовой оси; если же 0< R < , то дополнительно исследуем еще две точки — концы интервала сходимости.
Пример 3. Найти область сходимости степенного ряда:
а) 
; б) 
; в) 
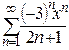; г) 
.
Решение.
а) Запишем ряд в виде 
, ряд по степеням х, коэффициент ряда 
, следовательно 
.
Вычислим радиус сходимости ряда:
= 
= 
=
= 
= 
.
R = . Область сходимости исходного ряда — вся числовая ось, 
.
б) - ряд по степеням х, а n= пn. Вычислим радиус сходимости ряда:
= 
= 
.
Ряд сходится в единственной точке х =0.
в)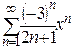 
- ряд по степеням х, 
; 
.
= 
= 
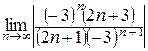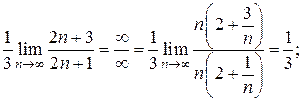
R =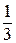 
, интервал сходимости 
.
Исследуем сходимость ряда в граничных точках указанного интервала.
При х = 
имеем ряд 
= 
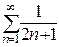. Он положительный, сравним его по второму признаку сравнения с расходящимся гармоническим рядом .
Получаем 
= 
.
Следовательно, ряды 
и 
эквивалентны в смысле сходи-мости, и значит, исследуемый ряд расходится и х = – 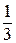не принадлежит области сходимости ряда.
При х = 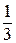получаем знакочередующийся ряд 
= 
.
Ряд из модулей его членов 
, как показано выше, расходится, т.е. абсолютной сходимости у знакочередующегося ряда нет. Исследуем ряд на условную сходимость по признаку Лейбница:
1) 
.
2) 
.
Значит, ряд сходится условно, х = 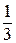принадлежит области сходимости ряда. Итак, область сходимости исходного ряда полуинтервал 
.
г) 
— ряд по степеням (х-х 0), х 0=2, ап = 
.
= 
.
Интервал сходимости (х 0- R; х 0+ R), т.е. (2-7; 2+7) или (-5; 9).
Исследуем сходимость на концах интервала.
При х = – 5 получим ряд 
. Он расходится по доста-точному признаку расходимости, так как 
.
Следовательно, точка х =-5 не принадлежит области сходимости ряда.
При х =9 получим ряд 
, который также расходится.
Поэтому областью сходимости исследуемого степенного ряда является интервал (-5; 9).
Разложение функций в ряд Маклорена
Если функция f (x) бесконечно дифференцируема в некоторой окрестности точки х =0, и все ее производные в этой окрестности ограничены одним числом: 
, п = 0,1,2…, то она раскладывается в ряд Маклорена
,
сходящийся в каждой точке этой окрестности к значению функции f (x).
Приведем разложения в ряды Маклорена (степенные ряды) элементарных функций с указанием области сходимости соответствующих рядов.
|
|
|
1) 
.
2) 
,
.
3) 
.
4) 
.
5) 
.
6) 
.
7) 
Пример 4. Разложить заданные функции в ряды по степеням (x-x 0) и указать области сходимости полученных рядов:
а) 
; х 0=0; б) 
; х 0=2.
Решение.
а) . Преобразуем заданную функцию: = 
.
Используя разложение
,
, при y= 4 x, найдем:
,
.
Следовательно, 
= 
, окончательно получаем:
= 
, .
б) ; х 0=2. Для того чтобы разложить функцию f (x) в ряд по степеням (х -2), представим ее в виде:
.
Используя разложение
,
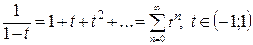при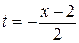 
, получим:
.
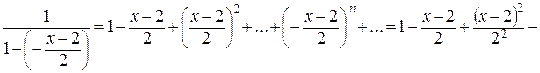
Область сходимости этого ряда определяется неравенством 
, т.е. 
или 0 < х < 4.
Следовательно, 
, и окончательно
получаем:
.
Полученный ряд сходится при 
.
Ряды Фурье
Пусть функция 
задана на отрезке 
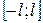и имеет период 
. Тригонометрическим рядом Фурье для функции 
называется ряд вида:
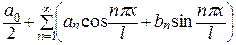, (1)
а 0, аn, bn называются коэффициентами ряда и вычисляются по формулам
, 
(2)
В тригонометрический ряд можно разложить функцию, удовлетворяющую определенным условиям, которые называются условиями Дирихле.
Функция на отрезке 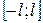удовлетворяет условиям Дирихле, если
1) она непрерывна на этом отрезке или имеет на нем конечное число точек разрыва первого рода (т.е. в точках разрыва существуют конечные односторонние пределы, но они не равны между собой);
2) функция на отрезке или не имеет точек экстремума, или имеет их конечное число;
3) существуют односторонние пределы 
и 
.
Сходимость тригонометрического ряда, составленного для функции f (x), определяется следующей теоремой.
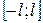Теорема Дирихле. Пусть функция определена для , имеет период и на отрезке удовлетворяет условиям Дирихле. Тогда ее ряд Фурье сходится на всей числовой оси, т.е. имеет сумму 
.
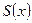При этом:
1) в точках непрерывности функции он сходится к самой функции, т.е. = ;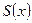
2) в точках разрыва функции х 0 сумма ряда равна полусумме односторонних пределов функции слева и справа, т.е. 
;
3) на концах отрезка 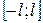сумма ряда определяется формулой:
.
Для четной функции = 
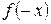все коэффициенты bn =0, и ряд Фурье имеет вид:
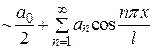, (3)
где 
, 
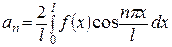n =1,2…,
т.е. четная функция разлагается в ряд Фурье только по косинусам.
Для нечетной функции =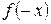 
а 0=0, все a n=0. Тогда
, 
(4)
Таким образом, нечетная функция разлагается в ряд Фурье толь-ко по синусам. Функцию f (x), заданную на интервале (0, l) можно произ-вольно продолжить на интервал (- l, 0), или как четную, или как нечетную, а затем разложить в неполный ряд Фурье, содержащий только косинусы или только синусы.
Алгоритм разложения функции , заданной графически на интервале (0,l), в неполный ряд Фурье
1) задать аналитически на (0, l);
2) доопределить функцию на (- l, 0) четным или нечетным образом;
3) проверить выполнение условий Дирихле на (- l,l);
4) определить коэффициенты ряда Фурье для полученной функции и записать ряд Фурье;
5) определить сумму ряда 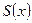для 
.
Пример 5. Функцию , заданную графически, разложить в ряд Фурье:
Рис. 1
Решение.
а) Функция, заданная графически на рис. 1а), аналитически описывается следующим образом:
= 
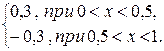
Чтобы получить разложение данной функции в ряд Фурье, содержащий только косинусы, продолжаем ее на соседний слева интервал 
четным образом (рис.2).
Рис. 2
Полученная функция на 
удовлетворяет условиям Дирихле: она имеет две точки разрыва первого рода x 1=-0,5 и x 2=0,5 и не имеет точек экстремума, поэтому ее можно разложить в сходящийся ряд Фурье. При этом bn =0, и по формуле (3), подставляя l =1, f (x)=0,3 в интервале (0;0,5) и f (x)=-0,3 в интервале (0,5;1), найдем
=
=0,6 
.
Использовали 
, 
для 
Если п четное, т.е. п =2 k,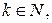 
то 
, т.е. a n=0 для четныхномеров n.
Если n нечетное, т.е. n= 2 k -1, 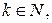то
,
т.к. по формулам приведения 
, а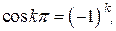 
.
При п =0 по формуле для а 0 получим:
.
Следовательно, искомое разложение данной функции в неполный ряд Фурье, содержащий только косинусы, следующее:
По теореме Дирихле полученный ряд сходится на всей числовой оси, При этом для суммы этого ряда S (x) выполняется
1. S (x)= f (x) во всех точках непрерывности функции f (x), т.е. при 
, и в разложении функции знак ~ можно заменить на знак =.
2. Определим S (x) в точках разрыва х 1=-0,5, х 2=0,5. 
,
.
3. На концах интервала, в точках x =- l и x = l, l =1 имеем
б) Функция, заданная графически на рис. 1б), аналитически описывается следующим образом:
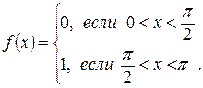
Чтобы получить разложение данной функции в ряд Фурье, содержащий только синусы, продолжим ее на 
нечетным образом (рис 3).
Рис. 3
Полученная функция на 
удовлетворяет условиям Дирихле: имеет две точки разрыва первого рода х 1 
, х 2 
и не имеет точек экстремума, поэтому ее можно разложить в ряд Фурье, сходящийся на всей числовой оси.
Функция нечетная, поэтому ап =0, п =0,1,2,…; bn вычислим по формуле (4), подставляя 
, 
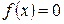в интервале 
и 
в интервале 
:
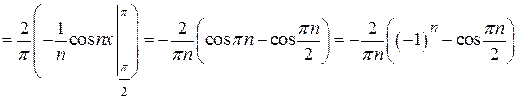, п =1,2,3,….
Следовательно, ряд Фурье для функции имеет вид:
~ 
= 
По теореме Дирихле полученный ряд сходится на всей числовой оси и имеет сумму S (x). При этом:
1. S (x)= f (x) для 
и в разложении знак ~ можно заменить на знак =.
2. В точках разрыва х 1= 
и х 2= сумма ряда равна:
,
.
3. На концах интервала в точках 
, 
имеем
.
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Теория вероятностей изучает закономерности для случайных явлений. Одним из основных терминов теории вероятностей является понятие случайного события. Событием называется всякий факт (исход), который в результате опыта (испытания, эксперимента) может произойти или не произойти. Каждому из таких событий можно поставить в соответствие определенное число, называемое его вероятностью, и являющееся мерой возможного совершения этого события. Например, отказ изделия - событие случайное, которое всегда имеет малую вероятность, если изделие обладает высокой эксплутационной надежностью.
Проведем классификацию основных типов событий. Совместные события – такие события, появление одного из которых не исключает возможности появления другого. Попарно несовместные события – такие события, появление одного из которых исключает любые возможности появления другого из остальных. Зависимые события – такие события, появление одного из которых влияет на появление другого события. Попарно независимыесобытия – такие события, появление одного из которых не влияет на появление другого события из остальных. Противоположные события это такие два события 
и 
, для которых наступление любого из них приводит к тому, что другое событие не наступает. Например, наступает , а событие
