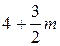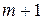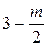|
Для подсчета номеров задач контрольных работ
|
|
|
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
для выполнения лабораторных, самостоятельных
и контрольных работ
по курсам «Информатика», «Вычислительная математика»
ЗАДАЧИ ПО ЧИСЛЕННЫМ МЕТОДАМ
Казань
Составители Ф.Г.Габбасов, Л.Б.Ермолаева,
Р.Ф.Гиззятов, С.К.Шафигуллина
УДК 621.313
Методические указания для выполнения лабораторных, самостоятельных и контрольных работ по курсам «Информатика», «Вычислительная математика». Задачи по численным методам. /Казанский государственный архитектурно-строительный университет. Сост.: Ф.Г.Габбасов, Л.Б.Ермолаева, Р.Ф.Гиззятов, С.К.Шафигуллина. Казань, 2011. – 26 с.
Данные методические указания содержат задания для лабораторных, самостоятельных и контрольных работ для студентов всех специальностей и направлений подготовки дневного и заочного отделений при изучении курса «Информатика» и «Вычислительная математика»
Рецензент – Р.Б.Салимов, доктор физ.-мат. наук, профессор
Казанский государственный
ã архитектурно-строительный
университет, 2011г.
№1. Численное решение нелинейных уравнений
Определить корни уравнения графически и уточнить один из них итерационными методами (методом деления отрезка пополам, методом Ньютона, методом простой итерации) с точностью 0,01:
| 1. | Х3 + 2X2 +2 = 0 | 19. | Х2 + 10 Х - 5=0 | |
| 2. | X3 – 2X +2= 0 | 20. | Х3 +13Х -13=0 | |
| 3. | Х3 + 3Х -1=0 | 21. | Х3 +7Х -7=0 | |
| 4. | Х3 + Х -3=0 | 22. | Х3 + 4Х - 2=0 | |
| 5. | Х3 + 2Х +4=0 | 23. | Х3 + 4Х - 4=0 | |
| 6. | (Х+1)2 =1/Х | 24. | Х3 + 8Х - 6=0 | |
| 7. | Х=(Х+1)3 | 25. | Х3 + 2,5Х - 4 =0 | |
| 8. | Х3 + 4Х - 4=0 | 26. | Х3 + 2,5Х - 5=0 | |
| 9. | Х3 + 6Х - 1=0 | 27. | Х3 + 5,5Х - 2=0 | |
| 10. | Х3 +12Х - 12=0 | 28. | Х3 + 7Х - 3=0 | |
| 11. | Х3 + 0,4Х - 1,2=0 | 29. | Х3 + 8Х - 5=0 | |
| 12. | Х3 + 0,5Х - 1=0 | 30. | Х3 + 15Х - 10=0 | |
| 13. | Х3 + 2Х - 4=0 | 31. | 
| |
| 14. | Х3 + 0,4Х + 2=0 | 32. | 
| |
| 15. | Х3 + 9Х - 11=0 | 33. | 
| |
| 16. | Х3 + 6Х +3=0 | 34. | 
| |
| 17. | Х3 + 5Х - 1=0 | 35. | 
| |
| 18. | Х3 + 9Х - 3=0 | 
| ||
| 37. | 
| 39. | 
| |
| 38. | Х3 - 5Х2 + 2Х + 8=0 | 40. | Х3 - 2Х2 - 5Х + 6=0 |
|
|
|
№2. Решение СЛАУ (систем линейных алгебраических уравнений)
Решить систему уравнений методом Гаусса:
| 1. | 
| 7. | 
| |
| 2. | 
| 8. | 
| |
| 3. | 
| 9. | 
| |
| 4. | 
| 10. | 
| |
| 5. | 
| 11. | 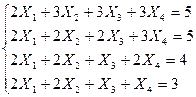
| |
| 6. | 
| 12. | 
| |
| 13. | 
| 20. | 
| |
| 14. | 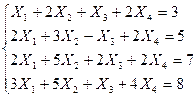
| 21. | 
| |
| 15. | 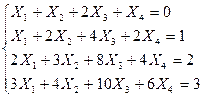
| 22. | 
| |
| 16. | 
| 23. | 
| |
| 17. | 
| 24. | 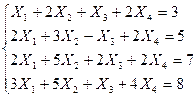
| |
| 18. | 
| 25. | 
| |
| 19. | 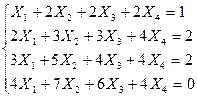
| 26. | 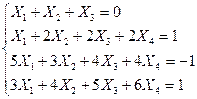
| |
| 27. | 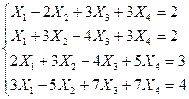
| 29. | 
| |
| 28. | 
| 30. | 
| |
| Решить СЛАУ итерационными методами с точностью 0,01 при заданном начальном приближении (0,7m; 1; 2; 0,5) | ||||
| 31. | 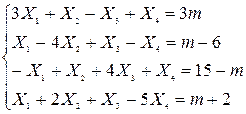
|

| ||
№3 Решение СЛАУ
Решить систему уравнений методом прогонки (или итерационным методом с точностью 0,01)
| 1. | 
| 4. | 
| |
| 2. | 
| 5. | 
| |
| 3. | 
| 6. | 
| |
| 7. | 
| 13. | 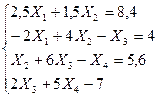
| |
| 8. | 
| 14. | 
| |
| 9. | 
| 15. | 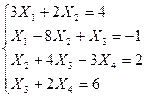
| |
| 10. | 
| 16. | 
| |
| 11. | 
| 17. | 
| |
| 12. | 
| 18. | 
| |
| 19. | 
| 25. | 
| |
| 20. | 
| 26. | 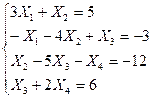
| |
| 21. | 
| 27. | 
| |
| 22. | 
| 28. | 
| |
| 23. | 
| 29. | 
| |
| 24. | 
| 30. | 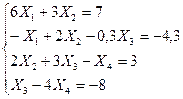
| |
| 31. | 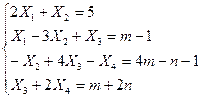
|

| ||
|
|
|
№4. Численное решение СНУ (систем нелинейных уравнений)
Решить систему нелинейных уравнений одним из итерационных методов (методом Ньютона, простых итераций, Зейделя) с точностью 0,01
| 1. | 
| 12. | 
| |
| 2. | 
| 13. | 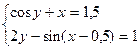
| |
| 3. | 
| 14. | 
| |
| 4. | 
| 15. | 
| |
| 5. | 
| 16. | 
| |
| 6. | 
| 17. | 
| |
| 7. | 
| 18. | 
| |
| 8. | 
| 19. | 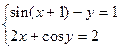
| |
| 9. | 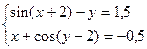
| 20. | 
| |
| 10. | 
| 21. | 
| |
| 11. | 
| 22. | 
| |
| 23. | 
| 27. | 
| |
| 24. | 
| 28. | 
| |
| 25. | 
| 29. | 
| |
| 26. | 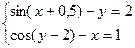
| 30. | 
| |
| 31. | 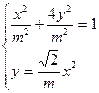
|
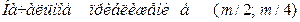
| ||
№5. Численное интегрирование
Вычислить интеграл по квадратурным формулам прямоугольников, трапеций, парабол
| 1. |
ò(2x2 -  )dx
-2 )dx
-2
| n=6 |
| 2. | ò(5x2 +x+1)dx -3 | n=6 |
| 3. |
ò (3x2 -  )dx )dx
| n=6 |
| 4. |
ò(x3 -  )dx )dx
| n=6 |
| 5. | ò (7+x-2x2)dx | n=6 |
| 6. |
ò (7x2 -3  )dx )dx
| n=6 |
| 7. |
ò (2x2 -2-  )dx )dx
| n=6 |
| 8. |
ò (5 x2 +  )dx )dx
| n=6 |
| 9. | ò (x3 +1)dx -2 | n=8 |
| 10. |
ò (2x2 +1-  )dx )dx
| n=8 |
| 11. |
ò (x2 +  -1)dx
- 2 -1)dx
- 2
| n=8 |
| 12. |
ò (x2 +2+  )dx )dx
| n=8 |
| 13. | ò(3x2 –x-1)dx | n=8 |
| 14. | ò (x3 +2)dx -1 | n=8 |
| 15. |
ò (2x2 +1- 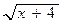 )dx
- 2 )dx
- 2
| n=8 |
| 16. |
ò(x2 -1,5  )dx )dx
| n=6 |
| 17. |
ò (7  +2x2)dx +2x2)dx
| n=6 |
| 18. |
ò (7x2 -3  )dx )dx
| n=6 |
| 19. |
ò (2x2 -2+  )dx )dx
| n=6 |
| 20. |
ò (5x2 -1+  )dx )dx
| n=6 |
| 21. |
ò (x2 +4+  )dx )dx
| n=6 |
| 22. | ò (x3 +3)dx | n=8 |
| 23. |
ò (2x2 -1+  )dx )dx
| n=6 |
| 24. |
ò (3x2 +2  )dx
-2 )dx
-2
| n=8 |
| 25. |
ò (x2 +2  )dx
-2 )dx
-2
| n=8 |
| 26. | ò (x2 +2x-1,5)dx -3 | n=8 |
| 27. |
ò(3x2 +1+  )dx
-3 )dx
-3
| n=6 |
| 28. |
ò (3x2 +5+  )dx )dx
| n=6 |
| 29. |
ò (7x+x2 -  )dx )dx
| n=6 |
| 30. |
ò (x2 -3  )dx )dx
| n=6 |
| 31. | 
| 
|
| 32. | 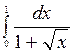
| |
| 33. | 
| 
|
| 34. | 
| 
|
| 35. | 
| |
| 36. | 
| 
|
| 37. | 
| |
| 38. | 
| |
| 39. | 
| |
| 40. | 
| |
|
|
|
№ 6. Решение Задачи Коши для дифференциального уравнения первого порядка методом конечных разностей
Решить задачу Коши методами Эйлера, модифицированным методом и методом Рунге-Кутты на заданном отрезке:
| 1. | y’=3+2 x2, | y(0)=2, | xÎ[0;1], | h=0,2 |
| 2. | y’= y- x2, | y(1)=0, | xÎ[1;2,2], | h=0,3 |
| 3. | y’=1-x2 +y, | y(1,1)=0, | xÎ[1,1;1,6], | h=0,1 |
| 4. | y’=y-7x2, | y(3)=3, | xÎ[3;5], | h=0,5 |
| 5. | y’=5-y+x2, | y(1)=1, | xÎ[1;5], | h=1 |
| 6. | y’=y-2x2 +3, | y(0)=4, | xÎ[0;1], | h=0,2 |
| 7. | y’=4-x2 +2y, | y(0)=1, | xÎ[0;1,2], | h=0,3 |
| 8. | y’= -8 +2x -y2, | y(1)=3, | xÎ[1;3], | h=0,4 |
| 9. | y’=2y-3x2, | y(4)=0, | xÎ[4,6], | h=0,5 |
| 10. | y’= x2 -2y, | y(-1)=1, | xÎ[-1;2], | h=0,3 |
| 11. | y’=7-xy, | y(-2)=0, | xÎ[-2;0], | h=0,5 |
| 12. | y’=2x2 +y, | y(2)=2, | xÎ[2;3,5], | h=0,5 |
| 13. | y’=5+x-y, | y(2)=1, | xÎ[2;4], | h=0,5 |
| 14. | y’=y-5x+1, | y(0)=2, | xÎ[0;3,2], | h=0,8 |
| 15. | y’=y-5x+1, | y(0)=2, | xÎ[0;3,2], | h=0,8 |
| 16. | y’=1-x+y, | y(0)=1, | xÎ[0;2,5], | h=0,5 |
| 17. | y’= y2 -5x, | y(-1)=1, | xÎ[-1;1], | h=0,4 |
| 18. | y’=x+2y, | y(0)= -1, | xÎ[0;2], | h=0,4 |
| 19. | y’=x+y+2, | y(1)=1, | xÎ[1;3], | h=0,5 |
| 20. | y’=3x+4y, | y(2)=1, | xÎ[2;5], | h=0,5 |
| 21. | y’=3+2x+y, | y(0)=2, | xÎ[0;1], | h=0,2 |
| 22. | y’= 2y- x2, | y(1)=0, | xÎ[1;2,2], | h=0,3 |
| 23. | y’=-x2 +y, | y(1,1)=0, | xÎ[1,1;1,6], | h=0,1 |
| 24. | y’=y-7x+2, | y(3)=3, | xÎ[3;5], | h=0,5 |
| 25. | y’=5-y+x2, | y(1)=1, | xÎ[1;5], | h=1 |
| 26. | y’=y-2x +3, | y(0)=4, | xÎ[0;1], | h=0,2 |
| 27. | y’=4-x2 +2y, | y(0)=1, | xÎ[0;1,2], | h=0,3 |
| 28. | y’= -8 +2x -y2, | y(1)=3, | xÎ[1;3], | h=0,4 |
| 29. | y’=2y-3x2, | y(4)=0, | xÎ[4,6], | h=0,5 |
| 30. | y’= x2 -2y, | y(-1)=1, | xÎ[-1;2], | h=0,3 |
| 31. | y’=5-x-2xy, | y(1)=2, | xÎ[2;4], | h=0,5 |
|
|
|
№7. Обработка результатов эксперимента
Методом наименьших квадратов найти зависимость между x и y:
| 1. |
| 4. |
| |||||||||||||||||||||||||
| 2. |
| 5. |
| |||||||||||||||||||||||||
| 3. |
| 6. |
| |||||||||||||||||||||||||
| 7. |
| 20. |
| |||||||||||||||||||||||||
| 8. |
| 21. |
| |||||||||||||||||||||||||
| 9. |
| 22. |
| |||||||||||||||||||||||||
| 10. |
| 23. |
| |||||||||||||||||||||||||
| 11. |
| 24. |
| |||||||||||||||||||||||||
| 12. |
| 25. |
| |||||||||||||||||||||||||
| 13. |
| 26. |
| |||||||||||||||||||||||||
| 14. |
| 27. |
| |||||||||||||||||||||||||
| 15. |
| 28. |
| |||||||||||||||||||||||||
| 16. |
| 29. |
| |||||||||||||||||||||||||
| 17. |
| 30. |
| |||||||||||||||||||||||||
| 18. |
| 31. |
| |||||||||||||||||||||||||
| 19. |
| 32. |
| |||||||||||||||||||||||||
| 33. |
| 37. |
| |||||||||||||||||||||||||
| 34. |
| 38. |
| |||||||||||||||||||||||||
| 35. |
| 39. |
| |||||||||||||||||||||||||
| 36. |
| 40. |
| |||||||||||||||||||||||||
| 41. |
|

| ||||||||||||||||||||||||||
№ 8. Решение краевой задачи для линейного дифференциального уравнения второго порядка методом конечных разностей
Используя метод конечных разностей, найти решение краевой задачи с шагом h=0,1
| 1. | y² + y’/x +2y=x y’(0,7)=0,5 y’(1)=1,2 | 5. | y² +2y-xy=x2 y’0,6)=0,7 y’(0,9)=1 | |
| 2. | y²-xy’+2y=x+1 y’(0,9)=2 y’(1,2)=1 | 6. | y²-3y’+y/x=1 y’(0,4)=2 y’(0,7)=0,7 | |
| 3. | y² +xy’ +y=x+1 y’(0,5)=1 y’(0,8)=1,2 | 7. | y²-3y’-y/x=x+1 y’(1,2)=1 y’(1,5)=0,5 | |
| 4. | y² +2y’-y/x=3 y’(0,2)=2 y’(0,5)=1 | 8. | y²-y’/2+3y=2x2 y’(1)=0,6 y’(1,3)=1 | |
| 9. | y²+1,5y’-xy=0,5 y’(1,3)=1 y’(1,6)=3 | 19. | y²+4y’-2y/x=1/x y’(1,2)=0,8 y’(0,9)=1 | |
| 10. | y²+2xy’-y=0,4 y’(0,3)=1 y’(0,6)=2 | 20. | y²-y’/2+4y/x=x/2 y’(1,3)=0,3 y(1,6)=0,6 | |
| 11. | y²-0,5xy’+y=2 y’(0,4)=1,2 y’(0,7)=1,4 | 21. | y²-y’/x-0,4y=2x y’(0,9)=1,7 y’(0,6)=0,6 | |
| 12. | y²+2y’/x-3y=2 y’(0,8)=1,5 y’(1,1)=3 | 22. | y²-2xy’-2y=0,6 y’(2)=1 y’(2,3)=1,5 | |
| 13. | y²+2x2 y’+ y y’(0,5)=1 y’(0,8)=3 | 23. | y²-y’/2x+0,8y=x y’(2)=1 y(1,7)=2 | |
| 14. | y²-3xy’+2y=1,5 y’(0,7)=1,3 y’(1)=2 | 24. | y²-y’/3+xy=2 y’(1)=1 y’(0,7)=1,6 | |
| 15. | y²-2y’/x-0,4y=4x y’(0,9)=1,5 y’(0,6)=0,6 | 25. | y²+2y’-y/x=2/x y’(1,1)=0,8 y’(0,8)=1 | |
| 16. | y²-xy’-4y=0,6 y’(2)=1 y’(2,3)=3 | 26. | y²-y’/4+2y/x=x/2 y’(1,3)=0,6 y(1,6)=0,3 | |
| 17. | y²-2y’/x+0,8y=x y’(2)=1 y(1,7)=2 | 27. | y² + y’/x +2y=x y’(0,7)=0,5 y’(1)=1,2 | |
| 18. | y²-y’/2+xy=4 y’(1)=1,5 y’(0,7)=2 | 28. | y²-xy’+2y=x+1 y’(0,9)=2 у'(1,2)=1 | |
| 29. | y² +xy’ +y=x+1 y’(0,5)=1 y’(0,8)=1,2 | 30. | y² +2y’-y/x=3 y’(0,2)=2 y’(0,5)=1 | |
№9 Интерполяция
Построить интерполяционный полином (Лагранжа и Ньютона) по заданным точкам
| 1. |
| 10. |
| |||||||||||||||||
| 2. |
| 11. |
| |||||||||||||||||
| 3. |
| |||||||||||||||||||
|
|
|