 |
После изучения тем разделов 1,2 студент должен выполнить контрольную работу №1.
|
|
|
|
ВЫСШАЯ МАТЕМАТИКА
Рабочая программа, методические указания и контрольные задания для студентов заочного отделения направление130400.65
(Богданова Л.П.)
Первый курс
Москва 2012г.
Преподавание высшей математики в высших учебных заведениях имеет целью, во-первых, формирование личности студента, развитие его интеллекта и способностей к логическому и алгоритмическому мышлению, и, во-вторых, обучение студента основным математическим методам, необходимым для анализа и моделирования экономических процессов.
Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом, которая состоит из следующих элементов: изучение материала по учебникам, решение задач, самопроверка, выполнение контрольных работ. В помощь студентам-заочникам университет организует чтение лекций, практические занятия. Кроме того, студент может обращаться к преподавателю с вопросами для получения письменной или устной консультации. Однако следует помнить, что помощь университета будет достаточно эффективной только при систематической и упорной работе. Завещающим этапом изучения отдельных частей курса высшей математики является сдача зачетов и экзаменов в соответствии с учебным планом.
Чтение учебника. Изучая материал по учебнику, можно переходить к следующему вопросу только после правильного понимания предыдущего, выполняя на бумаге все вычисления и вычерчивая имеющиеся в учебнике графики. Особое внимание следует обращать на определения основных понятий. Следует подробно разбирать примеры, которые поясняют такие определения, и уметь строить аналогичные примеры самостоятельно. Необходимо помнить, что каждая теорема состоит из предположений и утверждений. Все предположения должны обязательно использоваться в доказательстве. Нужно добиваться точного представления о том, в каком месте доказательства использовано каждое предположение теоремы.
|
|
|
При изучении материала по учебнику полезно вести конспект, в котором рекомендуется выписывать определения, формулировки теорем, формулы, определения и т.п.
Решение задач. Чтение учебника должно сопровождаться решением задач, для чего рекомендуется завести специальную тетрадь. При решении задач нужно обосновывать каждый этап, исходя из теоретических положений курса. Полезно до начала вычислений составить краткий план. Решения задач и примеров следует излагать подробно, вычисления располагать в строгом порядке, отделяя вспомогательные от основных. Решение каждой задачи должно доводиться до ответа, требуемого условием задачи. Решение задач определенного типа нужно продолжать до приобретения твердых навыков в их решении.
Самопроверка. После изучения определенной темы по учебнику и решения достаточного количества соответствующих задач студенту рекомендуется воспроизвести по памяти определения, выводы формул, формулировки и доказательства теорем. Иногда недостаточность усвоения материала выясняется только при дальнейшем его изучении. В этом случае надо вернуться назад и повторить плохо усвоенный раздел.
Важным критерием усвоения теории является умение решать задачи на пройденный материал. Однако здесь следует предостеречь студента от весьма распространенной ошибки, заключающейся в том, что благополучное решение задач воспринимается студентом как признак усвоения теории и правильное решение задачи получается в результате применения механически заученных формул без понимания существа дела.
Консультации. Если в процессе работы над изучением теоретического материала или при решении задач у студента возникают вопросы, разрешить которые самостоятельно не удается, то он может обратиться к преподавателю для получения от него письменной или устной консультации. В своих запросах студент должен точно указать, в чем он испытывает затруднение. Если он не разобрался в теоретических объяснениях или в доказательстве теоремы, то необходимо указать какой это учебник, где рассмотрен затрудняющий студента вопрос и что именно его затрудняет.
|
|
|
Контрольные работы. В процессе изучения курса высшей математики студент должен самостоятельно выполнить ряд контрольных работ, главная цель которых - оказать помощь студенту в его работе над материалом. При выполнении контрольных работ необходимо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки. Каждая контрольная работа должна быть выполнена в отдельной тетради в клетку. В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, учебный номер (шифр), номер контрольной работы, название дисциплины; здесь же следует указать название учебного заведения, дату выполнения работы и адрес студента.
В работу должны быть включены все задачи, указанные в задании строго по положенному варианту. Вариант задания выбирается по последней цифре шифра. Например, студент с шифром 998641 выполняет в контрольной работе следующие задачи первого варианта №№ 1, 11, 21, 31, 41, 51,61,71,81.
Решения задач должны быть расположены в порядке возрастания номеров, указанных в заданиях. Перед решением каждой задачи надо полностью выписать ее условие. В том случае, если несколько задач, из которых студент выбирает свой вариант, имеют общую формулировку, следует заменить общие данные конкретными, взятыми из своего варианта. Необходимо объяснять и мотивировать все действия по ходу решения и делать необходимые чертежи.
На собеседовании по каждой контрольной работе проверяется самостоятельность выполнения студентом контрольной работы, а также выясняется его готовность к сдаче зачета или экзамена.
Методические указания. Курс высшей математики разбит на темы, в которых даны ссылки на литературу, рекомендуемую для изучения и задачи для самостоятельного решения, Номера в квадратных скобках обозначают учебники из приведенного списка литературы.
|
|
|
После указателя литературы по каждой теме рабочей программы приводится перечень знаний и умений, которыми должен обладать студент, изучивший соответствующую тему. Студент может получить на кафедре высшей математики методические разработки по отдельным разделам курса.
ЛИТЕРАТУРА
1. Бугров Я.С., С.М. Никольский. Дифференциальное и интегральное исчисление. М.: Наука, 1980, 1984, 1988.
2. Бугров Я.С., С.М. Никольский. Элементы линейной алгебры и аналитической геометрии. М.: Наука, 1980, 1984, 1988.
3. Д.В. Клетенник. Сборник задач по аналитической геометрии. М.:Наука, 1986.
4. П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. Высшая математика в упражнениях и задачах. Ч.1,2. М.: Высшая школа, 1986 г.
5. Н.С. Пискунов. Дифференциальное и интегральное исчисление для ВТУЗов. Т.1,2. М.: Наука, 1976, 1985.
6. Сборник задач по математике для ВТУЗов. Линейная алгебра и основы математического анализа. (Под ред. А.В. Ефимова и Б.П. Демидовича). М.: Наука, 1971, 1980.
РАЗДЕЛ 1. Элементы линейной алгебры и аналитической геометрии.
ТЕМА 1.1. Матрицы и определители. Сложение и умножение матриц. Определители квадратных матриц и их свойства. Обратная матрица. Ранг матрицы. Свойства определителей.
[1], § 1-3.
[2], задачи №№ 1204, 1206, 1211-1216, 1252-1256.
[3], задачи №№ 222-228, 435, 436, 437.
Знать: что называется матрицей; виды матриц: матрица-строка, матрица-столбец, нулевая матрица, квадратная матрица порядка n, единичная матрица; что такое ранг матрицы; какие преобразования матрицы называются эквивалентными; что называется определителем, алгебраическим дополнением; свойства определителей.
Уметь: складывать и умножать матрицы; находить ранг матрицы; находить транспонированную и обратную матрицы; вычислять определители любого порядка.
После изучения тем 1.1 студент рекомендуется решить одну из задач вашего варианта из № 1-10.
ТЕМА 1.2. Системы линейных и алгебраических уравнений. Правило Крамера. Решение систем уравнений матричным методом. Теорема Кронекера-Капелли. Метод Гаусса.
|
|
|
[1], § 4.
[2], задачи №№ 1207, 1210, 1236-1246, 1249, 1250.
[3], задачи №№ 446-449.
Знать: какая система называется совместной; что значит решить систему; правило Крамера и метод Гаусса решения систем; теорему Кронекера-Капелли; матричный способ решения систем уравнений.
Уметь: решать системы уравнений при помощи правила Крамера, матричным способом и методом Гаусса.
После изучения тем 1.2 студент рекомендуется решить одну из задач вашего варианта из №№ 11-20.
ТЕМА 1.3. Векторы на плоскости и в пространстве. Линейная зависимость векторов, базис, n-мерные векторные пространства. Скалярное, векторное и смешанные произведения векторов.
[1], §§ 5, 6, 12, 14, 16, 17.
[2], задачи №№ 748, 750, 751, 761, 768, 792, 794, 809, 824.
[3], задачи №№ 248, 252, 255, 269, 270, 273, 280-285.
Знать: определение вектора; свойства векторов; определение коллинеарных и компланарных векторов; условие коллинеарности и компланарности векторов; определение базиса и размерности линейных векторных пространств; что такое скалярное, векторное, смешанное произведение векторов.
Уметь: находить базис и размерность векторных пространств; устанавливать коллинеарность и компланарность векторов; находить модуль вектора, скалярное, векторное и смешанное произведение векторов; находить угол между векторами, площадь треугольника, объем параллилипипеда, точку деления отрезков в данном отношении.
ТЕМА 1.4.Аналитическая геометрия на плоскости. Различные виды уравнения прямой. Геометрический метод решения системы неравенств. Линии второго порядка: окружность, эллипс, гипербола, парабола. Понятие о квадратичных формах и способах их приведения к каноническому виду. Полярная система координат.
[1], §§ 8, 24.
[2], задачи №№ 210, 213, 215, 227, 319, 351, 393, 418.
[3], задачи №№ 17, 18, 26, 44-48, 71, 72, 100, 102, 105, 116, 119, 144, 149, 155, 156, 171, 172.
Знать: различные виды уравнения прямой; условия параллельности и перпендикулярности прямых; определение эллипса, гиперболы и параболы; формулы перехода от декартовых к полярной системе координат.
Уметь: находить точку пересечения двух прямых; угол между прямыми; находить по каноническому уравнению эллипса и гиперболы координаты фокусов и эксцентриситет; находить по каноническому уравнению параболы координаты фокусов и уравнение директрисы; решать системы неравенств; записывать уравнения кривых в полярной системе координат, если известны их уравнения в декартовой системе координат.
После изучения тем 1.3 и 1.4 рекомендуем решить из задачи Вашего варианта из №№ 21-30.
|
|
|
ТЕМА 1.5. Аналитическая геометрия в пространстве. Уравнение плоскости. Нормальный вектор плоскости. Уравнение плоскости, проходящей через три данные точки. Общие, канонические и параметрические уравнения прямой линии в пространстве. Направляющий вектор прямой. Угол между прямой и плоскостью. Уравнение поверхности в пространстве. Цилиндрические поверхности. Сфера, конусы, эллипсоид, гиперболоиды, параболоид. Цилиндрическая и сферическая системы координат.
[1], §§ 9, 10.
[2], задачи №№ 913, 916, 921, 925, 972, 993, 1010, 1029.
[3], задачи №№ 302, 304, 307, 333, 341, 344.
Знать: общее уравнение плоскости в пространстве; что такое нормальный вектор плоскости; канонические уравнения прямой линии в пространстве; что такое напрвляющий вектор прямой; условия параллельности и перпендикулярности прямых и плоскостей.
Уметь: находить уравнение плоскости, проходящей через три данные точки; находить уравнение прямой, проходящей через две данные точки; определять точку пересечения прямой и плоскости; находить уравнение прямой, проходящей через данную точку перпендикулярно плоскости.
РАЗДЕЛ 2. Введение в математический анализ.
Элементы высшей алгебры.
ТЕМА 2.1. Множество вещественных чисел. Функция. Область ее определения. Способы задания. Основные элементарные функции, их графики. Класс элементарных функции. Метод преобразования графиков функций.
[3], задачи №№ 617-620.
[5], гл. 1, §§ 1,9. Упражнения к главе 1: №№ 1-3, 9-17, 39. [6], задачи №№ 151-156, 237-239, 369.
Знать: Определение переменной величины; возрастающие, убывающие, монотонные, ограниченные функции; способы задания функции; основные элементарные функции и их графики; определение сложных и обратных функций.
Уметь: находить область определения функции; строить графики элементарных функций деформацией графиков основных элементарных функций.
После изучения темы 2.1 рекомендуем решить одну из задач Вашего варианта из №№ 31-40.
ТЕМА 2.2. Числовые последовательности. Существование предела монотонной ограниченной последовательности. Предел функции в точке и в бесконечности. Пределы монотонных функций. Бесконечно малые величины. Сравнение бесконечно малых. Первый и второй замечательные пределы.
[3], задачи №№ 657-660, 669-672, 682, 692, 693.
[5], гл. 2, §§ 1-8, 11. Упражнения к главе 2: №№ 1-24.
[6], задачи №№ 411-413, 418-420, 437, 440, 471-475.
Знать: определение предела последовательности; предела функции в точке; бесконечно малые величины и их основные свойства; свойства пределов; первый и второй замечательные пределы.
Уметь: находить простейшие пределы при помощи искусственных приемов и первого и второго замечательных пределов.
После изучения темы 2.2 можно приступить к решению одной из задач Вашего варианта из №№ 41-50.
ТЕМА 2.3.Непрерывность функции в точке. Необходимое и достаточное условия непрерывности функции в точке. Непрерывность основных элементарных функций. Функции непрерывные на отрезке. Свойства функций, непрерывных в точке и на отрезке.
[3], задачи №№ 726-735.
[5], гл. 2, §§ 9, 10.
[6], задачи №№ 687-691, 729-731, 717, 718.
Знать: три определения непрерывности функций в точке; свойства непрерывных функций в точке и на отрезке; классификацию точек разрыва.
Уметь: определять области непрерывности функции и точки разрыва первого и второго рода.
После изучения темы 2.3 рекомендуем решить одну из задач Вашего варианта из №№ 51-70.
ТЕМА 2.4. Комплексные числа. Модуль и аргумент комплексного числа. Алгебраическая и тригонометрическая формы комплексные числа. Формула Эйлера. Показательная форма комплексного числа. Извлечение корней из комплексных чисел.
[5], гл. 7, §§ 1-3, 5. Упражнения к главе 7: №№ 81-100.
Знать: определение и свойства комплексных чисел; формулу Эйлера.
Уметь: записывать комплексные числа в алгебраической, тригонометрической и показательной формах; складывать, умножать и делить комплексные числа, извлекать корень из комплексного числа.
После изучения темы 2.4 можно приступить к решению одной из задач Вашего варианта № 71-80.
ТЕМА 2.5. Многочлены. Теорема Безу. Основная теорема алгебры. Разложения многочлена с действительными коэффициентами на линейные и квадратичные множители. Разложение рациональных дробей на простейшие.
[5], гл. 7, §§ 6-8. Упражнения к главе 7: №№ 14-16.
Знать: теорему Безу; основную теорему алгебры; теоремы о корнях многочленов с действительными коэффициентами.
Уметь: разлагать многочлена коэффициентами на множители; разлагать рациональные дроби на сумму простейших дробей.
После изучения темы 2.4 можно приступить к решению одной из задач Вашего варианта № 81-90.
После изучения тем разделов 1,2 студент должен выполнить контрольную работу №1.
КОНТРОЛЬНАЯ РАБОТА № 1.
Задачи №№ 1-10. Решить систему линейных уравнений методом Гаусса.
1. 
2. 
3. 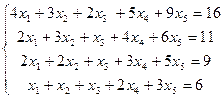
4. 
5. 
6. 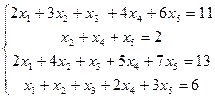
7. 
8. 
9. 
10. 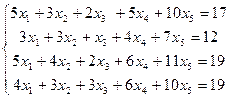
Задачи №№ 11-20. Решить систему линейных уравнений: а) по правилу Крамера; б) средствами матричного исчисления.
11.  12.
12. 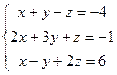
13.  14.
14. 
15.  16.
16. 
17. 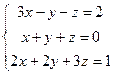 18.
18. 
19.  20.
20. 
Задачи №№ 21-30. Даны координаты вершин пирамиды А1А2А3А4. Сделать чертеж и найти: 1) длину ребра А1А2; 2) косинус угла между ребрами А1А2 и А1А4; 3) площадь грани А1А2А3; 4) уравнение грани А1А2А3; 5) уравнение высоты, опущенной из вершины А4 на грань А1А2А3; 6) объем пирамиды.
21. А1 (3,1,4), А2 (-1,6,1), А3 (-1,1,6), А4 (0,4,-1)
22. А1 (3,3,9), А2 (-6,9,1), А3 (1,6,3), А4 (8,5,8)
23. А1 (3,5,4), А2 (5,8,3), А3 (1,9,9), А4 (6,4,8)
24. А1 (2,4,3), А2 (7,6,3), А3 (4,9,3), А4 (3,6,7)
25. А1 (9,5,5), А2 (-3,7,1), А3 (5,7,8), А4 (6,9,2)
26. А1 (0,7,1), А2 (4,1,5), А3 (4,6,3), А4 (3,9,8)
27. А1 (5,5,4), А2 (3,8,4), А3 (3,5,10), А4 (5,8,2)
28. А1 (6,1,1), А2 (4,6,6), А3 (4,2,0), А4 (1,2,6)
29. А1 (7,5,3), А2 (9,4,4), А3 (4,5,7), А4 (7,9,6)
30. А1 (6,6,2), А2 (5,4,7), А3 (2,4,7), А4 (7,3,0).
Задачи №№ 31-35.Построить график функции  преобразованием графика функции
преобразованием графика функции  .
.
31.  32.
32. 
33.  34.
34. 
35. 
Задачи №№ 36-40. Построить график функции  преобразованием графика функции
преобразованием графика функции  .
.
36. 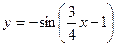 37.
37. 
38.  39.
39. 
40. 
Задачи №№ 41-50. Найти пределы функций, не пользуясь правилом Лопиталя.
41. а)  б)
б) 
в)  г)
г) 
42. а)  б)
б) 
в)  г)
г) 
43. а)  б)
б) 
в)  г)
г) 
44. а)  б)
б) 
в)  г)
г) 
45. а)  б)
б) 
в)  г)
г) 
46. а)  б)
б) 
в)  г)
г) 
47. а)  б)
б) 
в)  г)
г) 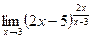
48. а)  б)
б) 
в)  г)
г) 
49. а)  б)
б) 
в)  г)
г) 
50. а) 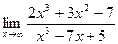 б)
б) 
в)  г)
г) 
Задачи №№ 51-60. Задана функция  и два значения аргумента
и два значения аргумента  и
и  .Требуется установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; в случае разрыва найти пределы в точке разрыва слева и справа и сделать схематический чертеж функции вблизи точки разрыва.
.Требуется установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; в случае разрыва найти пределы в точке разрыва слева и справа и сделать схематический чертеж функции вблизи точки разрыва.
51.  . 52.
. 52. 
53.  54.
54. 
55.  56.
56. 
57. 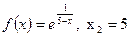 58.
58. 
59.  60.
60. 
Задачи №№ 61-70. Функция  задана различными аналитическими выражениями в различных областях изменения независимой переменной. Найти точки разрыва функции, если они существуют и построить ее график.
задана различными аналитическими выражениями в различных областях изменения независимой переменной. Найти точки разрыва функции, если они существуют и построить ее график.
61.  62.
62. 
63.  64.
64. 
65. 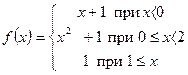 66.
66. 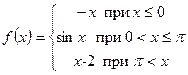
67.  68.
68. 
69.  70.
70. 
Задачи №№ 71-80. Представить комплексные числа  в показательной форме и вычислить выражения
в показательной форме и вычислить выражения  . Ответ записать в алгебраической форме.
. Ответ записать в алгебраической форме.
71.  .
.
72. 
73. 
74. 
75. 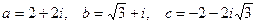
76. 
77. 
78. 
79. 
80. 
Задачи №№ 81-90. Разложить рациональную дробь на простейшие.
81.  82.
82. 
83.  84.
84. 
85.  86.
86. 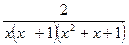
87.  88.
88. 
89.  90.
90. 
РАЗДЕЛ 3. Дифференциальное исчисление функций одной и многих переменных.
ТЕМА 3.1. Функция, дифференцируемая в точке. Дифференциал и производная функции. Правило нахождения производной и дифференциала. Производная сложной и обратной функции. Производная функции, заданной неявно или в параметрическом виде. Уравнение касательной и нормали к графику функции.
[2], гл. 4,8.
[4], гл. 3. §§ 1-10, 12, 13, 15, 20, 21, 26.
[5], задачи №№ 5.21-5.28, 5.33, 5.37, 5.39, 5.43, 5.47, 5.59, 5.63, 5.83, 5.85, 5.89, 5.327, 5.239, 5.284, 5.286.
Знать: определение производной, ее геометрический и механический смысл; правило дифференцирования суммы, произведения, частного двух функций, а также сложной и обратной функции; производные элементарных функций; определение дифференциала, его геометрический смысл; уравнения касательной и нормали к кривой.
Уметь: доказать теорему о связи непрерывности и дифференцируемости функции; находить производные функции; доказать теоремы о производной суммы, произведения и частного двух дифференцируемых функций; находить уравнения касательной и нормали к графику кривой в данной точке; находить дифференциал функции.
После изучения темы 3.1 рекомендуется решить одну из задач Вашего варианта из №№ 91-100.
ТЕМА 3.2. Производные и дифференциалы высших порядков; инвариантность формы первого дифференциала; дифференцирование функции, заданной параметрическими уравнениями.
[2], гл. 4, 9, 10,11.
[4], гл. 3, 11, 16-18, 22-25.
[5], задачи №№ 5.184-5.187, 5.188, 5.190, 5.218, 5.225, 5.226, 5.231, 5.233, 5.308.
Знать: правило дифференцирования функции, заданной неявно; правило нахождения производной функции, функции, заданной параметрическими уравнениями; теорему об инвариантности формы первого дифференциала; механический смысл второй производной.
Уметь: находить вторую производную функции.
После изучения темы 3.2 можно приступить к решению одной из задач Вашего варианта №№ 101-110.
ТЕМА 3.3. Точки экстремума функции. Теоремы Ферма, Роля, Лангража, Коши. Правило Лопиталя. Формулы Тейлора и Маклорена с остаточным членом в форме Лангража и Пеано. Представление по формуле Маклорена функций  .
.
[2], гл. 4. §§ 12-16.
[4], гл. 4. §§ 1-7.
[5], задачи №№ 5.317, 5.318, 5.329, 5.330, 5.334, 5.339, 5.340, 5.343, 5.368, 5.379, 5.391.
Знать: определение точки экстремума функции; теоремы Роля, Лангража, Коши, правило Лопиталя формулы Тейлора и Маклорена с остаточным членом в форме Лангража и Пеано.
Уметь: доказывать теоремы Ферма, Роля, Лангража, Коши; применять правило Лопиталя для нахождения пределов; разлагать в ряд Маклорена элементарные функции; оценивать ошибку при замене функции ее разложением по формуле Маклорена с конечным числом слагаемых.
ТЕМА 3.4. Условие монотонности функции. Экстремум функции. Наибольшее и наименьшее значения функций, дифференцируемых на отрезке; точки перегиба; асимптоты функции; общая схема исследования функции и построения ее графика.
[2], гл. 4. §§ 17-22.
[4], гл. 5. §§ 1-10.
[5], задачи №№ 5.404-5.410, 5.418, 5.438, 5.445, 5.457, 5.462, 5.465, 5.484, 5.500, 5.512.
Знать: определение выпуклости графика функции, точки перегиба, необходимые и достаточные условия монотонности функции, существование экстремума, выпуклости графика функции; правило нахождения наибольшего и наименьшего значений функции, дифференцируемой на отрезке; схему исследования функции.
Уметь: доказывать теоремы о необходимых и достаточных условиях экстремума функции; определять интервалы монотонности функции, интервалы выпуклости графика функции; находить асимптоты графика, находить наибольшее и наименьшее значения функции на отрезке; находить точки перегиба графика функции; строить эскизы графиков функции.
После изучения тем 3.3 и 3.4 рекомендуем решить одну из задач Вашего варианта из №№ 110--120.
ТЕМА 3.5. Понятие функции нескольких переменных. Непрерывность. Частные производные. Полный дифференциал. Производная по направлению. Градиент. Касательная плоскость и нормаль к поверхности. Частные производные высших порядков. Экстремум функции нескольких переменных. Условный экстремум. Метод множителей Лангража.
[2], гл. 8. §§ 11-17, 19.
[4], гл. 8. §§ 1-12, 14, 15, 17, 18.
[5], задачи №№ 7.4, 7.8, 7.32, 7.58, 7.60, 7.95-7.97, 7.101, 7.140, 7.142, 7.187, 7.193, 7.201-7.207, 7.213, 7.233 (а,б,в).
Знать: определение непрерывности и частной производной функции нескольких переменных; теорему о равенстве смешанных производных второго порядка у дифференцируемой функции двух переменных; определение градиента, его свойства; определение экстремума функции нескольких переменных; необходимый и достаточный признаки существования экстремума функции; определение выпуклого множества и выпуклой функции; определение выпуклого множества и выпуклой функции.
Уметь: находить частные производные любого порядка; находить градиент и производную по направлению в данной точке; приближенно находить значение функции, заменяя ее приращение дифференциалом; находить дифференциал функции двух переменных; находить точки экстремума, а также наибольшее и наименьшее значения функции двух переменных в замкнутой области.
Литература. [3], гл. 10, § 1-6.
Упражнения к гл. 10: 1-7, 8-101, 102-126, 127-146.
[4], задачи 6.15-6.28, 6.44-6.60, 6.114-6.143.
После изучения темы 3.5 рекомендуем решить одну из задач Вашего варианта из №№ 130--160.
Знать: определения первообразной и неопределенного интеграла; свойства неопределенного интеграла; таблицу интегралов.
Уметь: интегрировать методом замены переменной, интегрировать по частям.
Тема 3.2
Литература. [3], гл. 10, § 7-14.
Упражнения к гл. 10: 152-169, 189-216, 170-188.
[4], задачи 6.158-6.180, 6.190-6.197, 6.218-6.227, 6.238-6.245.
Знать: определения первообразной и неопределенного интеграла; свойства неопределенного интеграла; таблицу интегралов.
Уметь: интегрировать методом замены переменной, интегрировать по частям.
Тема 3.3
Литература. [3], гл. 11, § 1-6.
Упражнения к гл. 11: 1-25.
[4], задачи 6.324-6.337, 6.380-6.385.
Знать: как вводится понятие определенного интеграла; геометрический смысл определенного интеграла; его свойства; условия существования определенного интеграла; формулу Ньютона-Лейбница.
Уметь: составлять интегральную сумму; применять на практике формулу Ньютона-Лейбница; проводить замену переменной в определенном интеграле.
Тема 3.4
Литература. [3], гл. 12, § 1-5.
Упражнения к гл. 12: 1-30, 37-48.
[4], задачи 6.453-6.457, 6.493-6.500, 6.535-6.544.
Уметь: вычислять площадь и длину дуги в декартовой прямоугольной и полярной системах координат; то же для функций, заданных параметрическими уравнениями; вычислять объем тел вращения в прямоугольной системе координат.
Тема 3.5
Литература. [3], гл. 11, § 8.
Упражнения к гл. 11: 44-50.
[4], задачи 6.583-6.600.
Знать: сущность методов приближенного вычисления определенного интеграла – методов прямоугольников, трапеций и метода Симпсона.
Уметь: вычислять приближенное значение определенного интеграла методами прямоугольников, трапеций и методом Симпсона.
Тема 3.6
Литература. [3], гл. 11, § 7.
Упражнения к гл. 11: 29-43.
[4], задачи 6.411-6.424, 6.433-6.441.
Знать: определение несобственных интегралов с бесконечными пределами, признаки их сходимости; определение несобственных интегралов от неограниченных функций, признаки их сходимости.
Уметь: вычислять несобственные интегралы с бесконечными пределами и несобственные интегралы от неограниченных функций или доказать их расходимость.
|
|
|


