Для чего нужна диафрагма

 

 

Посмотрите внутрь объектива, и вы увидите в нем устройство, состоящее из нескольких тонких лепестков дуговой формы, расположенных по кругу, – это диафрагма (рис. 14).

 

 

Рис. 14. Диафрагма

 

С помощью специального привода (движка или рифленого кольца, опоясывающего оправу объектива) эти лепестки можно свести к центру объектива и тем самым уменьшить его действующее отверстие. Но с уменьшением действующего отверстия уменьшается светосила объектива и увеличивается выдержка при съемке. К чему же такое устройство?

Если на заре фотографии, когда не было хороших объективов, пользовались диафрагмой, – это понятно: диафрагма позволяла улучшить резкость изображения на краях снимка. Но зачем она теперь, когда современные объективы и так, без всякой диафрагмы, дают отличное, вполне резкое изображение по всему полю кадра? Зачем диафрагмировать объектив, если это не дает ничего, кроме ненужного увеличения выдержки?

Диафрагма крайне необходима, и пользоваться ею приходится очень часто. И вот почему.

В подавляющем большинстве случаев нам приходится фотографировать объекты, расположенные не в одной плоскости, а имеющие какую‑ то протяженность в глубь пространства или состоящие из нескольких планов, расположенных на разном расстоянии от фотоаппарата.

Рассуждая теоретически, получить на одном снимке резкое изображение предметов, разно удаленных от фотоаппарата, невозможно, поскольку каждому расстоянию от предмета до объектива соответствует определенное расстояние от объектива до пленки, при котором изображение предмета получается резким. Практически же такая съемка не только возможна, но успешно осуществляется на каждом шагу. В чем же причина такого явления? И нет ли здесь какого‑ то противоречия между теорией и практикой?

Конечно, никакого противоречия нет. Секрет заключается в особенностях нашего зрения. Когда мы фотографируем одновременно несколько предметов, расположенных на разном расстоянии от объектива, то, конечно, не все они получаются на снимке одинаково резкими. Наиболее резким будет изображение того предмета, по которому произведена наводка на резкость. Изображение всех других предметов, расположенных ближе и дальше, теоретически получается нерезким, но нерезкость эта иногда бывает настолько незначительной, что человеческий глаз не в состоянии ее обнаружить. Понятно, что с увеличением расстояния между предметом, по которому произведена наводка на резкость, и предметами, расположенными ближе и дальше, нерезкость изображения последних постепенно возрастает и в конце концов становится заметной на глаз, но в известных пределах она совершенно незаметна, что и позволяет фотографировать с достаточной резкостью многоплановые объекты.

Свойство объектива практически резко изображать на одном снимке предметы, расположенные от него на разном расстоянии, называется глубиной резкости объектива, а расстояние между передней и задней границами резкости – глубиной резкоизображаемого пространства.

 

 

Рис. 15. Диафрагма позволяет увеличить глубину резко изображаемого пространства: 1 – снимок сделан с наводкой на чайник, 2 – на чашку, 3 – на сахарницу при уменьшенном отверстии диафрагмы

 

В разных случаях глубина резко изображаемого пространства получается разной и зависит от ряда условий, но во всех случаях она тем больше, чем меньше действующее отверстие объектива, т. е. отверстие диафрагмы. Таким образом, диафрагмируя объектив, можно увеличить глубину резко изображаемого пространства, и именно в этом заключается главное назначение диафрагмы.

На рис. 15 приведены три снимка одного и того же сюжета. Сфотографированы три предмета: чайник, сахарница и чашка, расположенные на столе на разном расстоянии от фотоаппарата. Первые два снимка сделаны при наибольшем отверстии диафрагмы, т. е. при полной светосиле объектива.

Первый снимок был сделан с наводкой на резкость на ближайший предмет. Два дальних предмета получились на снимке нерезко, причем нерезкость дальнего предмета сильнее, чем среднего. Это понятно: дальний предмет расположен дальше от плана наводки, чем средний.

На втором снимке наводка была сделана на дальний предмет. Нерезко получились два ближних. Не лучше обстояло дело, если бы мы произвели наводку на средний предмет, так как в этом случае нерезко получились бы дальний и ближний предметы.

Когда же наводка была сделана на средний предмет, но отверстие диафрагмы было уменьшено, удалось получить на снимке резкое изображение всех трех предметов (третий снимок). Таково действие диафрагмы. Чем же оно объясняется?

Как мы уже говорили в главе 1, изображение предмета, рисуемое объективом, состоит из мельчайших точек. Опытом установлено, что изображение это представляется нам резким, если диаметр каждой такой точки[6] не превышает 0, 1 мм. Изображение каждой точки образуется конически сходящимся пучком лучей, падающих из объектива на поверхность пленки, и находится в точке пересечения этих лучей, т. е. в вершине светового конуса (рис. 16). При этом диаметр полученных точек обычно очень мал и иногда не превышает 0, 01 мм. Поэтому, если поместить пленку строго точно в плоскости пересечения лучей, то изображение точки безусловно будет резким.

 

 

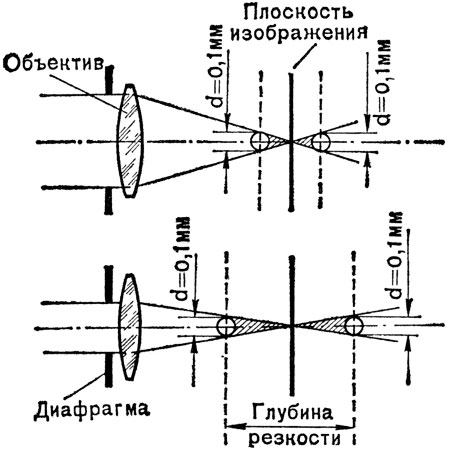
Рис. 16. Схема действия диафрагмы

 

Попробуем теперь сместить пленку, т. е. придвинуть ее к объективу или, наоборот, отнести ее немного дальше, как обозначено на рисунке пунктиром. Как в том, так и в другом случае пленка будет пересекать конус лучей и вместо точки на ней появится световой кружок. Теоретически изображение станет в этом случае нерезким, но если диаметр светового кружка не превышает 0, 1 мм, то нам такое изображение будет казаться резким. Таким образом, практически без потери резкости расстояние между объективом и поверхностью пленки можно в каких‑ то пределах менять. А это значит, что если поместить пленку точно в плоскость пересечения лучей, идущих от плоскости наводки, то можно получить на пленке резкое изображение предметов, расположенных ближе и дальше плоскости наводки, конечно, в известных пределах. Расстояние, в пределах которого можно перемещать пленку, и характеризует глубину резкости. Последняя, очевидно, тем больше, чем больше это расстояние.

Теперь нетрудно понять, почему с уменьшением диафрагмы глубина резкости, а с ней и глубина резко изображаемого пространства увеличиваются. Как видно из нижнего рисунка, диафрагма уменьшает угол схождения лучей, делает конус лучей острее, вследствие чего расстояние между допустимыми пределами перемещения пленки становится больше.

Однако не следует думать, что глубина резко изображаемого пространства зависит только от величины отверстия диафрагмы. Это может привести вас к неверному пользованию диафрагмой, а в конечном счете к ошибкам во время съемки.

Глубина резко изображаемого пространства зависит и от величины фокусного расстояния объектива. При прочих равных условиях съемки она тем больше, чем меньше фокусное расстояние объектива.

 

 

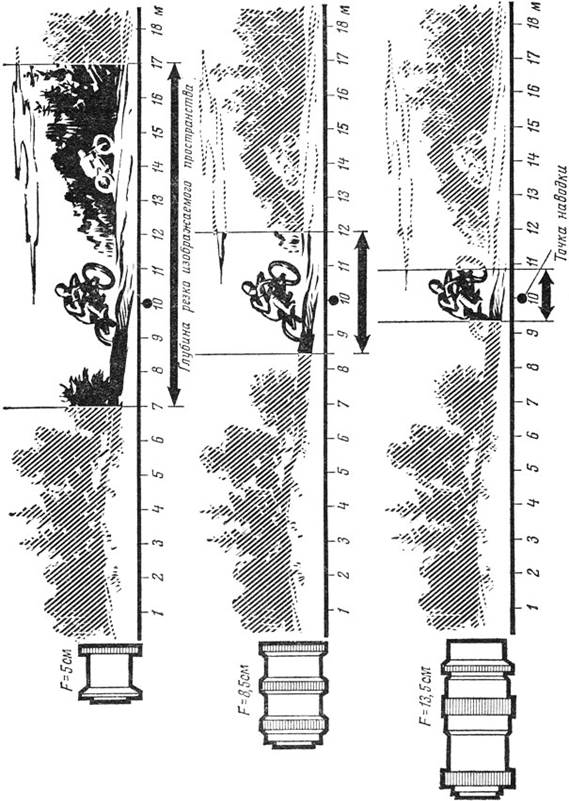
Рис. 17. Чем больше фокусное расстояние объектива, тем меньше глубина резко изображаемого пространства

Рис. 17 показывает, как изменяется глубина резко изображаемого пространства при съемке объективами с разными фокусными расстояниями. Во всех трех случаях изображенные на рисунке объективы имели равные относительные отверстия и были наведены на одно и то же расстояние – 10 м. Черным кружком обозначена точка наводки на резкость, а стрелкой – глубина резко изображаемого пространства.

Поскольку в дальнейшем вам, возможно, придется пользоваться объективами с разными фокусными расстояниями, это обстоятельство нельзя упускать из виду.

В практической работе вам придется учитывать и еще одну величину, существенно влияющую на глубину резко изображаемого пространства, – расстояние до точки наводки. С увеличением расстояния от фотоаппарата до точки наводки на резкость глубина резко изображаемого пространства прогрессивно возрастает.

На рис. 18 приведен пример, показывающий, как изменяется глубина резко изображаемого пространства (она обозначена стрелкой) при съемке объективом F = 50 мм с относительным отверстием 1: 3, 5 и при наводке на 5, 7 и 10 м.

 

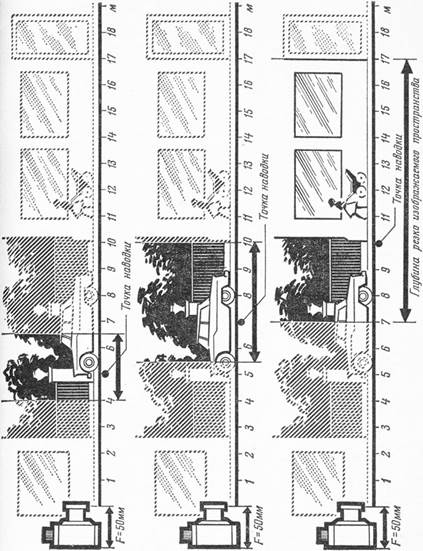
Рис. 18. С увеличением расстояния до точки наводки глубина резко изображаемого пространства возрастает

 

Для объективов с другими фокусными расстояниями и при других относительных отверстиях абсолютная величина глубины резко изображаемого пространства будет, конечно, иной, но во всех случаях она тем больше, чем дальше находится точка наводки.

Наконец, есть еще одна величина, оказывающая влияние на глубину резко изображаемого пространства. Это степень резкости изображения. Фотографические снимки в большинстве случаев увеличивают, а при всяком увеличении, как известно, резкость изображения снижается, при этом тем сильнее, чем больше кратность увеличения. Кратность же увеличения тесно связана с размерами негативов. Чтобы получить отпечаток формата 18 x 24 см с негатива 6 x 9 см, последний надо увеличить линейно в три раза. Для получения отпечатка такого же формата с негатива размером 24 x 36 мм последний придется увеличить линейно примерно в семь раз.

Таким образом, если для негатива 6 x 9 см достаточна резкость, при которой каждая точка изображения может иметь в диаметре 0, 1 мм, то для негативов формата 24 х 36 мм она уже недостаточна. Здесь необходима резкость, в два‑ три раза более высокая, т. е. диаметр каждой точки не должен превышать 0, 02‑ 0, 03 мм.

С повышением требований к степени резкости глубина резко изображаемого пространства, естественно, уменьшается. Поэтому, если вам случится когда‑ нибудь сравнивать два объектива с одинаковыми фокусными расстояниями, а глубина резкости у них окажется разной, не удивляйтесь этому.

Например, существуют два объектива: «Юпитер‑ 9» с фокусным расстоянием 8, 5 см и «Индустар‑ 24» с фокусным расстоянием 10, 5 см. Казалось бы, что у первого из них глубина резкости должна быть больше, так как фокусное расстояние его меньше. На самом же деле все наоборот. Объясняется это тем, что объектив «Юпитер‑ 9» предназначен для фотоаппаратов формата 24 x 36 мм, а «Индустар‑ 24» устанавливается на фотоаппаратах формата 6 x 9 см и требования к степени резкости для него менее строгие.

Итак, глубина резкости и связанная с ней глубина резко изображаемого пространства зависит от четырех условий: величины фокусного расстояния объектива, величины отверстия диафрагмы, расстояния до точки наводки и степени резкости изображения.

Не следует думать, что глубина резкости зависит от номинальной светосилы объектива. Снимая при прочих равных условиях объективом с относительным отверстием 1: 4, 5, вы получите такую же глубину резко изображаемого пространства, как и объективом с относительным отверстием 1: 2 или 1: 1, 5, задиафрагмированным до относительного отверстия 1: 4, 5. Высокая первоначальная светосила объектива никаких преимуществ в этом смысле не дает.

Поскольку с уменьшением отверстия диафрагмы уменьшается светосила объектива и увеличивается выдержка, необходимо знать, какая светосила или какое относительное отверстие соответствует тому или иному отверстию диафрагмы. Иначе пользоваться диафрагмой невозможно.

 

 

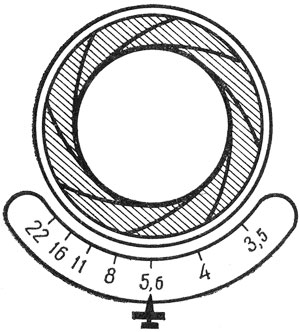
Рис. 19. На шкале диафрагмы обозначены знаменатели относительных отверстий

 

Поэтому диафрагма снабжается шкалой с цифровыми делениями, показывающими величины относительных отверстий при установке указателя диафрагмы на то или иное деление этой шкалы (рис. 19). Но для того, чтобы не загромождать шкалу многими цифрами, и поскольку в числителе относительных отверстий всегда стоит единица, на шкалу наносят только знаменатели относительных отверстий. Так, цифра 4 на шкале диафрагмы означает относительное отверстие 1: 4, цифра 5, 6 – относительное отверстие 1: 5, 6 и т. д.

Исходное, т. е. крайнее, деление шкалы диафрагмы всегда соответствует наибольшему относительному отверстию объектива и поэтому совпадает с ним. Так, если относительное отверстие объектива 1: 2, то первое деление шкалы диафрагмы будет обозначено числом 2. Далее обычно следует такой ряд цифр:

 

 

Это принятый в Советском Союзе международный стандартный ряд величин относительных отверстий. Откуда же взялись эти на первый взгляд случайные цифры?

Выдержка при съемке обратно пропорциональна светосиле объектива. Светосила же, как мы знаем, выражается квадратом относительного отверстия. Нетрудно подсчитать, что квадрат каждого последующего относительного отверстия шкалы диафрагмы (представляющий собой не что иное, как светосилу) в два раза меньше, чем квадрат предыдущего. Таким образом, переход от одного деления шкалы диафрагмы к другому, рядом стоящему, изменяет светосилу объектива, а следовательно, и выдержку в два раза. Вы, конечно, согласитесь, что при переходе с одного отверстия диафрагмы на другое это значительно облегчает нахождение новой выдержки. Очевидно, что с переходом от меньшей цифры шкалы диафрагмы к большей светосила уменьшается, а выдержка увеличивается, и наоборот.

Таким же расчетом вам придется руководствоваться и при выборе фотоаппарата, если вы захотите сравнить светосилу объективов двух фотоаппаратов, имеющих разные относительные отверстия, например 1: 2 и 1: 4. Для этого вам придется сначала возвести в квадрат относительные отверстия этих объективов, а затем уже разделить большую из полученных величин на меньшую. В нашем примере ход решения этой задачи выглядит так:

 

(¹/₂)² = ¹/₄; (¹/₄)² = ¹/₁₆; ¹/₄: ¹/₁₆ = ¹⁶/₄ = 4,

 

т. е. светосила первого объектива в четыре раза больше, чем второго.

Можно решить эту задачу и более просто: возвести в квадрат только знаменатели относительных отверстий и большее из полученных чисел разделить на меньшее или, что еще проще, разделить больший знаменатель относительного отверстия на меньший и возвести в квадрат полученное частное.

Бывает так, что при расчете фотографического объектива не всегда удается получить относительное отверстие, совпадающее с каким‑ нибудь числом стандартного ряда. Встречаются объективы с относительными отверстиями 1: 1, 5; 1: 3, 5; 1: 4, 5 и др., отсутствующими в стандартном ряду.

В таких случаях в качестве второй величины на шкале диафрагмы ставят ближайшее к нему число стандартного ряда.

Например, если объектив имеет относительное отверстие 1: 3, 5, то первым делением шкалы диафрагмы будет 3, 5, а следующим – 4. Далее будут следовать числа стандартного ряда.

В таких случаях при переходе от первого деления шкалы к второму светосила объектива, а с ней и выдержка уменьшаются не в два раза, а меньше. В приведенном примере выдержка изменится в 1, 3 раза, так как

 

3, 5² = 12, 25; 4²= 16; 16: 12, 25 = 1, 3.

 

Практически выдержку в этом случае можно не менять.

 

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: