 |
Список используемых источников
|
|
|
|
ПРЕОБРАЗОВАНИЯ И СОСТАВЛЕНИЯ СХЕМ И ТАБЛИЦ
1.1 Таблица истинности для исходной функции
Разбор функции по действиям. В порядке последовательности от слагаемых до конечной функции. Вычисление значений при определённых комбинациях переменных представлено в таблице 1.
Таблица 1– Таблица истинности исходной функции
| A | B | C | B̅ | C˅A | B̅→(C˅A) | (B̅→(C˅A))B | (B̅→(C˅A))BA |
1.2 Совершенная конъюнктивная нормальная форма (СКНФ)
Выделены строки, в которых функция равна 0. Для каждой строки дизъюнкция переменных записывается по следующему алгоритму: если значение переменной в данной строке равно 0, то записать саму переменную, а если значение равно 1, то записать отрицание этой переменной. Значения пременных приведены в таблице 1.
f(A,B,C)=(A˅B˅C)(A˅B˅C̅)(A˅B̅˅C)(A˅B̅˅C̅)(A̅˅B˅C)(A̅˅B˅C̅).
Совершенная дизъюнктивная нормальная форма (СДНФ)
Выделены строки, в которых функция равна 1. Для каждой строки конъюкция переменных записывается по следующему алгоритму: если значение переменной в данной строке равно 1, то записать саму переменную, а если значение переменной равно 0, то записать отрицание этой переменной. Значения переменных приведены в таблице 1. [1]
f(A,B,C)=ABC̅˅ABC.
1.3 Упрощение (минимизация) для СДНФ
Используя основные правила и законы логики упрощаем функцию СДНФ.[2]
f(A,B,C)=ABC̅˅ABC = AB, по закону слияния, где (A+B̅)(A+B)=A, после применения этого закона получено данное выражение.
|
|
|
1.4 Таблица истинности для упрощённой СДНФ
Составление таблицы истинности для функции вида СДНФ после упрощения (таблица 2).
Таблица 2 – Таблица истинности для СДНФ
| A | B | С |  C
| ABC |  ABC
| AB |
1.5 Построить логические схемы для упрощённой СДНФ и исходной функции
Построение схемы используя теоретические материалы из методического пособия и образцы схем.
Для СДНФ (после минимизации) логическая схема изображена на рисунке 1.
Рисунок 1 – Логическая схема СДНФ (после минимизации)
Для исходной функции логическая схема представлена на рисунке 2.
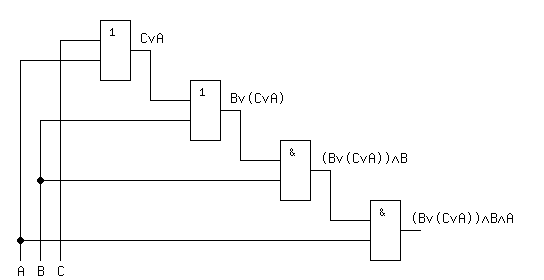
Рисунок 2 – Логическая схема исходной функции
ПРОГРАММИРОВАНИЕ
2.1 Составить программу для упрощённой функции полученной в пункте 1.1 на языке Си
Подробное упрощение исходного выражения f(A,B,C)=(B̅→(C˅A))BA. Использованы основные законы логики для упрощения функции.
1. f(A,B,C)=(B̅→(C˅A))BA, исходная функция.
2. f(A,B,C)=(B̿˅(C˅A))BA, по правилу замены импликации, где A→B=A̅+B, получено двойное отрицание.
3. f(A,B,C)=(B˅C˅A)BA, по закону двойного отрицания, где 
, получено данное выражение.
4. f(A,B,C)=(BB˅CB˅AB)A, раскрытие скобок умножением на В.
5. f(A,B,C)=(B˅CB˅AB)A, по закону идемпотентности BB=B, получено данное выражение. По закону поглощения, где A+AB=A, получено следующее выражение.
6. f(A,B,C)=(B˅AB)A, по закону поглощения, где A+AB=A, получено следующее выражение.
7. f(A,B,C)=BA, данное выражение является конечным и далее не упрощается.
После упрощения данной функции составлен исходный код представленный ниже. Использованы данные полученные из методического пособия [3].
|
|
|
#include<stdio.h>
#include<conio.h>
#include<math.h>
int main(void)
{ int a,b,c,F;
jh:printf ("\n\t Vasha logicheskaya funkciya F=A*B ");
printf ("\n Vvedite A,B (A,B mogut prinimat' znacheniya tol'ko 0 ili 1)\n");
printf ("\n\t 0 - lojnoe, 1 - istinnoe.\n");
scanf("%d,%d",&a,&b);
if(a!=0&&a!=1||b!=0&&b!=1){printf ("Neverno vvedeni dannie. Povtorite vvod\n"); goto jh;} else
F=a*b;
printf ("\OTveT:%d",F);
getch();
}
После составления исходного кода произведен запуск программы и проверка программы на наличие ошибок (рис 4)
Рисунок 4 – Запуск и проверка программы
2.1 Составить блок-схему алгоритма
Использованы определённые компоненты и данные для схемы, составлена блок схема для данной упрощённой функции полученной в п. 1.1 (рис. 5). [4]
- начало, конец алгоритма.
- исходные данные.
- выполнение действий.
- условие.
- переход к следующему действию.
Рисунок 5 – Блок схема алгоритма
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
|
|
|
