 |
Часть 1. Расчет и анализ надежности системы восстанавливаемых объектов
|
|
|
|
1.1 Введение
Системы электроснабжения относятся к классу сложных технических систем и определяются множеством свойств, из которых к числу важнейших относится свойство надежности технической системы.
Надежная работа устройств системы электроснабжения является необходимым условием обеспечения качественной и устойчивой работы железнодорожного транспорта. Анализ и обеспечение работоспособного состояния систем электроснабжения на этапах проектирования и эксплуатации – сложная задача, для решения которой используется математический аппарат теории надежности.
Термины и определения, используемые в теории надежности, регламентированы ГОСТ 27.002-89 «Надежность в технике. Термины и определения». Надежность – свойство объекта выполнять заданные функции, сохраняя во времени и в заданных пределах значения всех эксплуатационных параметров.
Надежность объекта характеризуется следующими основными состояниями и событиями:
· Исправность – состояние объекта, при котором он соответствует всем требованиям, установленным нормативно-технической документацией.
· Работоспособность – состояние объекта, при котором он способен выполнять заданные функции, сохраняя значения основных параметров, установленных НТД.
· Предельное состояние – состояние объекта, при котором его применение (использование) по назначению недопустимо или нецелесообразно.
· Повреждение - событие, заключающееся в нарушении исправного состояния объекта при сохранении его работоспособного состояния.
· Отказ – событие, заключающееся в нарушении работоспособного состояния объекта.
· Критерий отказа – отличительный признак или совокупность признаков, согласно которым устанавливается факт возникновения отказа.
|
|
|
Для некоторых объектов предельное состояние является последним в его функционировании, т.е. объект снимается с эксплуатации, для других – определенной фазой в эксплуатационном графике, требующей проведения ремонтно-восстановительных работ. В связи с этим, объекты могут быть разделены на два класса:
· невосстанавливаемые, для которых работоспособность в случае возникновения отказа, не подлежит, или по каким либо причинам нецелесообразна;
· восстанавливаемые, работоспособность которых может быть восстановлена, в том числе и путем замены элементов.
К числу невосстанавливаемых объектов можно отнести, например, электронные и электротехнические детали (диоды, сопротивления, конденсаторы, изоляторы и другие элементы конструкций). Объекты, состоящие из многих элементов, например, трансформатор, выключатель, электронная аппаратура, являются восстанавливаемыми, поскольку их отказы связаны с повреждениями одного или нескольких элементов, которые могут быть отремонтированы или заменены. В ряде случаев один и тот же объект в зависимости от особенностей, этапов эксплуатации или назначения может считаться восстанавливаемым или невосстанавливаемым.
Введенная классификация играет важную роль при выборе моделей и методов анализа надежности.
Надежность является комплексным свойством, включающим в себя, в зависимости от назначения объекта или условий его эксплуатации, ряд составляющих свойств, в соответствии с ГОСТ 27.002-89:
· безотказность;
· долговечность;
· ремонтопригодность;
· сохраняемость.
Безотказность – свойство объекта непрерывно сохранять работоспособность в течение некоторой наработки или в течение некоторого времени.
Долговечность – свойство объекта сохранять работоспособность до наступления предельного состояния при установленной системе технического обслуживания и ремонтов.
|
|
|
Ремонтопригодность – свойство объекта, заключающееся в его приспособленности к предупреждению и обнаружению причин возникновения отказов, поддержанию и восстановлению работоспособности путем проведения ремонтов и технического обслуживания.
Сохраняемость – свойство объекта непрерывно сохранять требуемые эксплуатационные показатели в течение (и после) срока хранения и транспортирования.
В зависимости от объекта, надежность может определяться всеми перечисленными свойствами или частью их.
Наработка – продолжительность или объем работы объекта, измеряемая в любых неубывающих величинах (единица времени, число циклов нагружения, километры пробега и т. п.).
Показатель надежности количественно характеризует, в какой степени данному объекту присущи определенные свойства, обусловливающие надежность.
Одним из основных показателей надежности является функция надежности:
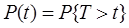
где: T – наработка до отказа, t – заданная наработка. Таким образом, функция надежности есть вероятность безотказной работы (ВБР) объекта на интервале (0, t).
Функция ненадежности определяется как вероятность отказа (ВО) объекта на интервале (0, t):
При анализе системы, состоящей из однотипных элементов с большим сроком службы, в большинстве практических случаев полагают, что вероятность безотказной работы элементов одинакова для всех элементов и подчиняется экспоненциальному закону:
где λ - интенсивность отказов (ИО) одного элемента: условная плотность вероятности возникновения отказа невосстанавливаемого объекта на бесконечно малом интервале времени при условии, что до этого момента отказ объекта не произошел. Напомним, что для экспоненциального закона ИО постоянна, что позволяет получить простые расчетные выражения.
При условии независимости отказов элементов, ВБР цепи из l последовательно соединенных элементов определится на основе теоремы умножения вероятностей:
где 
- интенсивность отказов цепи.
При параллельном соединении n элементов (блок «один вход- один выход») ВО блока определяется следующим выражением:
|
|
|
Методика расчетов надежности, применяемая для систем электроснабжения, основывается на общей теоретической базе. При этом учитываются существенные, с точки зрения анализа и расчета показателей надежности, структурные и функциональные особенности рассматриваемых систем.
1.2 Формулировка задачи
· Определить оценки показателей надежности (коэффициент готовности) для элементов системы, показанной на схеме замещения, по данным статистки отказов и восстановления за период эксплуатации N лет, с учетом паспортных данных, приведенных в Приложении 1 и 2.
· Составить модель структуры сети для анализа надежности логико-вероятностным методом и определить значения ее показателей. Рассчитать и построить графики зависимости коэффициента готовности системы и вероятности отказа питания от каждого источника генерации на L последующих лет эксплуатации, с разбивкой по кварталам.
· Сделать выводы о необходимости технического обслуживания по критерию минимально допустимого уровня надежности.
Условия расчета: пренебречь ненадежностью источников питания и шин 110 и 10 кв. Законы распределения отказов и восстановления принять экспоненциальными, отказы элементов - независимы. Для двухцепных ЛЭП учитывать только отказ 2-х цепей. Для трансформаторов учитывать только восстановление аварийным ремонтом.
Принять в данной задаче, что пропускная способность всех устройств сети выше максимальной нагрузки.
1.3 Теоретические сведения
В поставленной задаче необходимо по статистике отказов устройств конкретной подстанции уточнить показатели надежности, соответствующие “априорным данным”, взятым из приложений 1 и 2, и представляющим собой средние значения, рассчитанные по ансамблю ретроспективных данных. По условиям задачи, следует выбрать данные для заданного номинального напряжения, видов отказов и ремонтов, и типов устройств. Для линий следует пересчитать табличные данные частоты отказов (откл/100 км в год) на фактическую длину ЛЭП.
Одним из распространенных методов учета новых данных является скользящее среднее:
|
|
|
хt = (1-g) · хt-1 + g · yt, (1.1)
где:
хt-1 – предыдущее (априорное) значение некоторого параметра х к моменту t,
хt - новое значение (оценка) того же параметра, полученная уточнением априорных данных по результатам прямых или косвенных измерений yt,
g - вес измерений yt..
В условиях данной задачи коэффициент g представляет собой отношение времени эксплуатации к суммарному времени накопления данных (временем восстановления в этой формуле пренебрегаем).
Примечания:
1) Элементы, ни разу не отказавшие, учитываются “априорными данными” из приложений 1 и 2.
2) Предполагается, что “возраст” априорных данных, приведенных в таблицах приложения – 15 лет.
3) Следует обратить внимание на размерность параметров: время t – [год], частота отказов (оценка интенсивности) l - [отключений / год], время наработки или восстановления - [10-3лет].
Так как известно, что распределение отказов и восстановления подчиняются экспоненциальному закону, то коэффициент готовности элементов равен [1]:
kг = t0/(t0+ tв ), (1.2)
где
t0 = 1/ λ, - наработка до отказа (при экспоненциальном законе распределения),
tв - время восстановления,
После простых преобразований получим:
kг =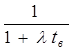 
(1.3)
До расчетов по формулам (1.2) или (1.3), следует предварительно оценить показатели надежности элементов схемы замещения, отказавших и восстановленных за период эксплуатации объекта. Для этого воспользуемся формулой (1.1):
g = N \ L;
λi* = (1-g) · λi + g ·(ni\N);
tвi* = (1-g) · tвi + g ·( );
| 
| (1.4) |
где: i – номер элемента, ni – число отказов i-го элемента за период эксплуатации, j- индекс,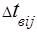 
- время восстановления i-го элемента при j-м отказе. Верхним индексом * отмечены оценки параметров – эти значения должны быть использованы в формуле (1.3).
Для построения модели структуры сети с целью анализа надежности и определения значений ее показателей следует применить логико- вероятностный метод [2]. Метод основан на приложении алгебры логики к описанию состояний работоспособности и восстановления системы.
Вероятность нахождения восстанавливаемой системы, представленной ЛФР, в работоспособном состоянии в момент времени t, определится выражением:
kГ (t) = P(Z = 1), (1.7)
при этом для каждого i-го элемента справедливо аналогичное выражение:
kГi (t) = P(xi = 1). (1.8)
При последовательном соединении n элементов:
P(Z = 1) = P(x1=1) P(x2=1)… P(xn=1) = 
. (1.9)
Тогда для восстанавливаемой системы, состоящей из n последовательных элементов:
kГ(t) = 
; λ(t) =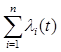 
; p(t) = 
. (1.10)
При параллельном соединении составим логическую функцию неработоспособности:
|
|
|
Q(t) = P(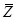
=1)= P(
=1)·P(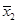
=1)… P(
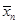=1) = 
= 
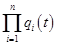, (1.11)
где qi(t) = 1- pi(t).
Приведенные формулы (1.5) – (1.11) позволяют построить ЛФР по заданной схеме электропитания, см. п. 1.4.
Зная зависимость kГ(t) и заданное значение минимально допустимого уровня надежности: минимально-допустимого коэффициента готовности kГдоп , можно оценить максимальный срок эксплуатации без технического обслуживания [5] по критерию:
kГ(t) > kГдоп (1.12)
Если существует момент времени tдоп, при котором нарушается неравенство (1.12), то, с точки зрения обеспечения заданного уровня надежности, следует назначить техническое обслуживание (планово-профилактическое) до момента tдоп. Если же tдоп = 0, то в выводах следует указать, что профилактическое техническое обслуживание необходимо провести до расчетного периода эксплуатации.
1.4 Расчет задания
Схема замещения подстанции показана на рис 1.1
Описание схемы и параметры расчета:
· Длина линий: Л1 = 31км; Л2 = 131 км. Линия Л2 – двухцепная.
· Выключатели: В1 и В3 – масляные, В2 и и В4 – воздушные.
· Период эксплуатации N = 6 лет; период прогнозирования L = 2 года.
· Минимально допустимый уровень надежности kГдоп = 0,84
Таблица 1.1 данные по элементам схемы
| Элемент | λ – частота отказов, откл/год | tв- ср. время восстановления, 10-3лет/отказ | Число отказов | Время восстановления 10-3лет/отказ |
| Паспортные данные | Статистика отказов | |||
| В1 | 0,01 | 2,5 | 2 | 12,7; 11,8 |
| В2 | 0,07 | 2,5 | 0 | - |
| В3 | 0,01 | 2,5 | 2 | 16,7; 17,8 |
| В4 | 0,07 | 2,5 | 1 | 29,6 |
| Л1 | 0,423 | 0,5 | 0 | - |
| Л2 | 0,572 | 3 | 0 | - |
| От1 | 0,013 | 0,4 | 0 | - |
| От2 | 0,013 | 0,4 | 0 | - |
| От3 | 0,013 | 0,4 | 0 | - |
| Т1 | 0,01 | 60,0 | 0 | - |
| Т2 | 0,01 | 60,0 | 3 | 85,2; 85,1; 59,1 |
| Т3 | 0,01 | 60,0 | 0 | - |
| Л1: | 1.41·(31км/100 км) = 0,437 откл/год; |
| Л2: | 0.44·(131 км/100 км) = 0,576 откл/год. |
Далее, по данным статистики отказов, следует рассчитать оценки частоты отказов и среднего времени их восстановления.
Приведем пример расчета для одного из отказавших элементов (трансформатор Т1):
· вес измерений определим как «коэффициент старения информации»:
g =6 /(6+15) = 0,286; (1- g) = 0,714;
· оценки параметров найдем по формулам (1.4) и (1.3):
λ*(В1) = (1- g) · λ(В1) + g · (2/6) =
= 0,714*0,01 + 0,286∙0,333 = 0,1025 откл/год;
t*в(В1) = (1- g) · tв(В1) + g ·[1/2*(12,7+11,8)] =
= 0,714*2,5 + 0,286 ∙12,25 = 5,29·10-3лет/отказ.
kг (В1) = 1 / (1+ 0,1025*5,29∙10-3) = 0,9995
Результаты расчета показателей по статистике отказов
| Элемент | Переменная xi | λ* – частота отказов, откл/год | t*в- ср. время восстановления 10-3лет/отказ | Кг -коэфф. готовности |
| В1 | x1 | 0,1025 | 5,29 | 0,99950 |
| В2 | x5 | 0,07 | 2,5 | 0,99983 |
| В3 | x23 | 0,102 | 6,72 | 0,99931 |
| В4 | x34 | 0,098 | 10,25 | 0,99900 |
| Л1 | x12 | 0,423 | 0,5 | 0,99979 |
| Л2 | x45 | 0,572 | 3 | 0,99829 |
| От1 | x26 | 0,013 | 0,4 | 0,99999 |
| От2 | x37 | 0,013 | 0,4 | 0,99999 |
| От3 | x48 | 0,013 | 0,4 | 0,99999 |
| Т1 | x6 | 0,01 | 60 | 0.99940 |
| Т2 | x7 | 0,15 | 64,71 | 0.99038 |
| Т3 | x8 | 0,01 | 60 | 0,99940 |
Исходя из заданной схемы замещения, составим ЛФР для 3-го узла, учитывая все возможные пути от источника к потребителю. Для этого преобразуем исходную схему к структурной для анализа надежности, введя дополнительные узлы и переменные состояния xi.
Переменные структурной схемы описаны в таблице соответствия 1.3.
Таблица 1.3. Соответствие параметров состояния структурной схемы элементам схемы замещения.
| x1: состояние выключателя В1 | x45: состояние линии Л2 |
| x12: состояние линии Л1 | x5: состояние выключателя В2 |
| x2: состояние шин 110 кв | x26: состояние отделителя От1 |
| x23: состояние выключателя ШСВ В3 | x6: состояние трансформатора Т1 |
| x3: состояние шин 110 кв | x37: состояние отделителя От2 |
| x34 : состояние выключателя ШСВ В4
| x7: состояние трансформатора Т2 |
| x48: состояние отделителя От3 | |
| x8: состояние трансформатора Т3 |
Рис 1.2. Структурная схема анализа надежности.
Рис 1.3. Схема представления ЛФР
Из схемы на рис 1.2. видно, что ЛФР системы представляет дизъюнкцию ЛФР шести путей электропитания (в индексе пути использованы только номера узлов структурной схемы):
Z = Z1-2-6 + Z1-2-3-7 + Z1-2-3-4-8 + Z5-4-8 + Z5-4-3-7 + Z5-4-3-2-6 (1.13)
Раскрывая ЛФР правой части (1.13), получим:
Z = (x1 x12 x2 x26 x6)+(x1 x12 x2 x23 x3 x37 x7)+(x1 x12 x2 x23 x3 x34 x4 x48 x8)+ +(x5 x45 x4 x48 x8)+(x5 x45 x4 x34 x3 x37 x7)+(x5 x45 x4 x34 x3 x23 x2 x26 x6).
Упростим данное выражение, учитывая, что x2 =1, x3 =1, x4 =1
Z = (x1 x12 x26 x6)+(x1 x12 x23 x37 x7)+(x1 x12 x23 x34 x48 x8)+(x5 x45 x48 x8)+
+(x5 x45 x34 x37 x7)+(x5 x45 x34 x23 x26 x6)= Z1-2· (Z2-6 + Z2-7+ Z2-8) + Z5-4 ·(Z4-8 + +Z4-7 + Z4-6) (1.14)
Структурная схема представления ЛФР в форме (1.14) показана на рисунке 1.3.
Раскроем выражения составляющих ЛФР в формуле (1.7) P(Z = 1), для ее конкретного представления (1.13) - (1.14) и заданного экспоненциального закона распределения:
· Для блоков последовательных элементов на рис. 1.3:
P(Z1-2 =1) = P(x1=1)·P(x12=1) = p1-2 =e-(λ1+λ12)t,
P(Z5-4 =1) = P(x5=1)·P(x45=1) = p5-4 = e-(λ5+λ45)t
· Для блоков параллельных элементов на рис. 1.3:
P(Z2-6 =1)= P(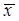
26 =1)·P( 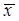6 =1) = q2-6 = 1- e-(λ6+λ26)t
P(Z2-7 =1)= P(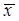 23 =1)·P( 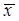37 =1) P( 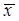7 =1) = q2-7 =1- e-(λ23+λ37+λ7)t
P(Z2-8=1)=P(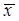 23 =1)·P( 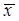34 =1)P( 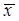48 =1) P( 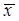8 =1)=q2-8=1- e-(λ23+λ34+λ48+λ8)t
P(Z4-8 =1)= P(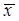 48 =1)·P( 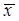8=1) = q4-8 = 1 - e-(λ8+λ48)t
P(Z4-7 =1)= P(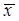 34 =1)·P( 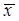37 =1) P( 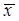7 =1) = q4-7 = 1- e-(λ34+λ37+λ7)t
P(Z4-6=1)= P(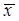 34=1)·P( 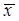23=1)P( 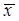26=1)P( 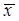6=1)=q4-6=1-e-(λ23+λ34+λ26+λ6)t
Введем промежуточные обозначения:
p2-6-7-8 = 1-q2-6-7-8 = 1- q2-6∙ q2-7 q2-8 - ВБР блока параллельных элементов Z2-6 + Z2-7 + Z2-8 ,
p4-8-7-6 = 1-q4-8-7-6 = 1- q4-8∙ q4-7 q4-6 - ВБР блока параллельных элементов Z4-8 + Z4-7 + Z4-6
q1* = 1 - p1-2∙ p2-6-7-8 - ВО питания на пути от узла №1 на схеме замещения,
q4* = 1 – p4-5∙ p4-8-7-6 - ВО питания на пути от узла №2 на схеме замещения и запишем окончательно:
Q = q1*∙ q4* ; kГ(t) = P(Z = 1) = 1 – Q. (1.15)
Расчеты, выполненные по полученным формулам, приведены в таблице 1.4. Данные таблицы характеризуют изменение составляющих ЛФР на заданном периоде предстоящей эксплуатации (L = 2 года) с поквартальной разбивкой. На рисунке 1.4. показаны графики изменения трех основных показателей надежности данной системы: q1*∙(t), q4*(t), kГ(t), построенные по данным табл.1.4. Такой вид изменения показателей во времени типичен для экспоненциального закона распределения.
Таблица 1.4 Расчет показателей надежности на двухлетний период эксплуатации (прогноз)
| Формула Z(*) | ∑ λ | 1-й год | 2-й год | ||||||
| 0,25 | 0,5 | 0,75 | 1 | 1,25 | 1,5 | 1,75 | 2 | ||
| p1-2 = e-(λ1+λ12)t | 0,5805 | 0,864914 | 0,748077 | 0,647022 | 0,559618 | 0,484022 | 0,418637 | 0,362085 | 0,313173 |
| p5-4 = e-(λ5+λ45)t | 0,642 | 0,851718 | 0,725423 | 0,617856 | 0,526239 | 0,448207 | 0,381746 | 0,32514 | 0,276927 |
| q2-6 = 1- e-(λ6+λ26)t | 0,023 | 0,005734 | 0,011434 | 0,017102 | 0,022738 | 0,028341 | 0,033912 | 0,039451 | 0,044958 |
| q2-7=1- e-(λ23+λ37+λ7)t | 0,265 | 0,064103 | 0,124097 | 0,180245 | 0,232794 | 0,281974 | 0,328002 | 0,371079 | 0,411395 |
| q2-8 = 1- e-(λ23+λ34+λ48+λ8)t | 0,223 | 0,054224 | 0,105509 | 0,154012 | 0,199885 | 0,243271 | 0,284304 | 0,323112 | 0,359816 |
| q4-8 = 1- e-(λ8+λ48)t | 0,023 | 0,005734 | 0,011434 | 0,017102 | 0,022738 | 0,028341 | 0,033912 | 0,039451 | 0,044958 |
| q4-7 = 1- e-(λ34+λ37+λ7)t | 0,261 | 0,063167 | 0,122344 | 0,177782 | 0,229719 | 0,278375 | 0,323958 | 0,366661 | 0,406667 |
| q4-6 = 1- e-(λ23+λ34+λ48+λ6) | 0,223 | 0,054224 | 0,105509 | 0,154012 | 0,199885 | 0,243271 | 0,284304 | 0,323112 | 0,359816 |
| p2-6-7-8 = 1- q2-6 ∙ q2-7∙ q2-8 | 0,99998 | 0,99985 | 0,999525 | 0,998942 | 0,998056 | 0,996838 | 0,99527 | 0,993345 | |
| p4-8-7-6 =1- q4-8 ∙ q4-7∙ q4-6 | 0,99998 | 0,999852 | 0,999532 | 0,998956 | 0,998081 | 0,996877 | 0,995326 | 0,993421 | |
| q1* = 1 - p1-2 ∙ p2-6-7-8 | 0,135103 | 0,252035 | 0,353285 | 0,440974 | 0,516919 | 0,582686 | 0,639627 | 0,688911 | |
| q4* = 1 – p4-5 ∙ p4-8-7-6 | 0,148299 | 0,274684 | 0,382433 | 0,474311 | 0,552653 | 0,619446 | 0,67638 | 0,724894 | |
| kГ (t)= 1 – q1* ∙ q4* | 0,979964 | 0,93077 | 0,864892 | 0,790842 | 0,714323 | 0,639057 | 0,567369 | 0,500612 | |
Изменение ВО питания и kг системы
Из таблицы и графиков видно, что критерий (1.12) нарушается уже в четвертом квартале 1-го года последующей эксплуатации:
kГ(0,75) > kГдоп > kГ(1), или: 0.8649 > 0,92 > 0,7908
поэтому tдоп = 0,5 и техническое обслуживание (профилактическое) следует назначить либо в конце второго квартала, либо в начале третьего квартала.
Структурная схема ЛФР в данном случае была несколько загрублена, более точное её представление, возможно, несколько уточнит ситуацию.
Рис 1.6. Схема представления ЛФР
Теперь представим ВБР согласно этой схемы:
· Для блоков последовательных элементов на рис. 1.4:
P(Z1-2 =1) = P(x1=1)·P(x12=1) = p1-2 =e-(λ1+λ12)t,
P(Z5-4 =1) = P(x5=1)·P(x45=1) = p5-4 = e-(λ5+λ45)t
P(Z2-3 =1) = P(x23=1)= p2-3 = e-λ23 t
P(Z3-4 =1) = P(x34=1) = p3-4 = e- λ34 t
· Для блоков параллельных элементов на рис. 1.4:
P(Z2-6 =1)= P(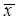
26 =1)·P( 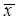6 =1) = q2-6 = 1- e-(λ6+λ26)t
P(Z2-7 =1)= P(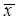 37 =1)·P( 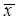7 =1) = q3-7 =1- e-(λ37+λ7)t
P(Z3-8=1)= P(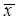 34 =1)·P( 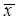48 =1)·P( 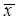8 =1) = q3-8 = 1- e-(λ34+λ48+λ8)t
P(Z4-8 =1)= P(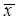 48 =1)·P( 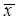8=1) = q4-8 = 1 - e-(λ8+λ48)t
P(Z3-6=1)= P(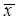 23=1)P( 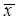26=1)P( 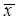6=1) = q4-6 =1-e-(λ23 +λ26+λ6)t
Введем промежуточные обозначения:
p3-7-8 = 1- q3-7-8 = 1- q3-7 ∙q3-8 - ВБР блока параллельных элементов Z3-7 + Z3-8
q2-7-8 = 1- p2-7-8 = 1- p2-3 ∙p3-7-8 - ВБР блока последовательных элементов Z2-3 и группы элементов Z3-7 + Z3-8
p3-6-7 = 1- q3-6-7 = 1- q3-6 ∙q3-7 - ВБР блока параллельных элементов Z3-7 + Z3-6
q4-6-7 = 1- p3-6-7 = 1- p4-3 ∙p3-6-7 - ВБР блока последовательных элементов Z4-3 и группы элементов Z3-7 + Z3-6
p2-6-7-8 = 1- q2-6-7-8 = 1- q2-6∙ q2-7-8 - ВБР блока параллельных элементов Z2-6 и группы элементов Z2-3 + Z3-7 + Z3-8
p4-8-7-6 = 1- q4-8-7-6 = 1- q4-8∙ q4-6-7 - ВБР блока параллельных элементов Z4-8 и группы элементов Z4-3 + Z3-7 + Z3-6
q1* = 1 - p1-2∙ p2-6-7-8 - ВО питания на пути от узла №1 на схеме замещения,
q4* = 1 – p4-5∙ p4-8-7-6 - ВО питания на пути от узла №2 на схеме замещения
и запишем окончательно:
Q = q1*∙ q4* ; kГ(t) = P(Z = 1) = 1 – Q. (1.15)
Таблица 1.5 Расчет показателей надежности на двухлетний период эксплуатации (прогноз)
Из таблицы и графиков видно, что критерий (1.12) нарушается уже в четвертом квартале 1-го года последующей эксплуатации:
kГ(0,75) > kГдоп > kГ(1), или: 0.875 > 0,84 > 0,805
поэтому tдоп = 0,5 и техническое обслуживание (профилактическое) следует назначить либо в конце второго квартала, либо в начале третьего квартала. В данном случае данные с загрублённой схемы и с развёрнутой схемы совпали.
Часть 2. Анализ надежности и резервирование технической системы.
2.1 Введение
В сложных технических устройствах без резервирования никогда не удается достичь высокой надежности, даже используя элементы с высокими показателями безотказности.
Система со структурным резервированием – это система с избыточностью элементов, т. е. с резервными составляющими, избыточными по отношению к минимально необходимой (основной) структуре и выполняющими те же функции, что и основные элементы. В системах с резервированием работоспособность обеспечивается до тех пор, пока для замены отказавших основных элементов имеются в наличии резервные.
По способу включения резервных элементов резервирование подразделяют на два вида:
· активное (ненагруженное) – резервные элементы вводятся в работу только после отказа основных элементов
· пассивное (нагруженное) – резервные элементы функционируют наравне с основными (постоянно включены в работу). Этот вид резервирования достаточно широко распространен, т.к. обеспечивает самый высокий коэффициент оперативной готовности.
Кратко остановимся на расчете надежности систем с ограничением по нагрузке.
Если условия функционирования таковы, что для работоспособности системы необходимо, чтобы по меньшей мере r элементов из n были работоспособны, то число необходимых рабочих элементов равно r, резервных – (n - r). Отказ системы наступает при условии отказа (n – r + 1) элементов. Число r, в общем случае, зависит от многих факторов, но в большинстве расчетов надежности требуется обеспечить пропускную (или нагрузочную) способность системы в заданном режиме эксплуатации. При этом, отказы можно считать независимыми только тогда, когда при изменении числа находящихся в работе элементов не наблюдается перегрузки, влияющей на возможность возникновения отказа. ВБР такой системы определяется с помощью биномиального распределения.
2.2 Формулировка задания
Для заданной основной схемы электротехнического объекта следует:
· Определить вероятность работоспособного состояния объекта для расчетного уровня нагрузки и построить зависимость данного показателя надежности от нагрузки.
· Обеспечить заданный уровень надежности объекта резервированием его слабых звеньев с учетом требований минимальной избыточности и стоимости резервирования.
2.3 Теоретические сведения
Для повышения надежности способом структурного резервирования (повышением избыточности) предлагается использовать элементы нескольких типов, отличающихся степенью надежности, пропускной способностью и стоимостью. При этом избыточными могут быть или уровни надежности, или уровни пропускной способности, или количество элементов. Допускается также обоснованный ввод дополнительных связей.
Предлагаемый способ оценки надежности сложной установки (объекта) относится к аналитическим методам. Он основывается на общей теореме о повторении опытов теории вероятностей, подчиняющейся теоремам сложения и умножения вероятностей, формуле полной вероятности и др. [3].
Предположим сначала, что установка состоит из n одинаковых бинарных элементов, состояния которых являются независимыми, совместными событиями. В качестве производящей функции при этом используется бином Ньютона:
(p[Z]+q[0])n =
p n[nZ] +Cn1p n-1 q[(n-1)Z] +Cn2p n--2 q[(n-2)Z]…+Cnmp n-m q m[(n-m)Z] +…qn[0]= = 
= 
= 1. (2.1)
Здесь р - вероятность работоспособного состояния каждого из элементов, образующих объект (установку). Производительность элемента обозначается буквой Z; q = 1-p - вероятность неработоспособного состояния элемента (производительность элемента при этом равна нулю). Слагаемые
(2.2)
представляют собой вероятности нахождения любых (п-т) элементов объекта в работоспособном состоянии, а т - в неработоспособном из-за их отказа; при этом (п-т)Z - суммарная производительность всех элементов в m-ом состоянии.
Всего состояний объекта в таком случае получается (n + 1), что намного меньше, чем 2n, если рассматривать состояния n элементов без группировки их по критерию мощности. Состояния (n + 1) составляют полную группу событий (соответствующих состояний) и поэтому сумма их вероятностей (см. формулу (2.1)) равна 1.
Для вычисления слагаемых в (2.2) можно воспользоваться рекуррентной формулой:
,
которая следует из отношения:
Pт+1 / Pт = 
/ 
,
и дает возможность использовать удобный алгоритм расчета вероятности следующего состояния по уже известной вероятности Pт предыдущего расчетного состояния.
Развитием этого метода является применение производящей функции вида:
S(Z) = 
, (2.3)
позволяющей рассчитывать надежность объекта, который состоит из разных по надежности элементов, отличающихся производительностью. Выражение (2.3) является более универсальным, чем (2.1), но расчеты состояний усложняются, так как должны быть перемножены между собой все двучлены и сгруппированы по одинаковой производительности (пропускной способности). Оценка работоспособности объекта в том или ином расчетном состоянии должна производиться в рамках рассматриваемого метода на основе составления и анализа так называемых структурных функций. Структурная функция - выражение, отображающее взаимосвязь групп элементов, соединенных последовательно или параллельно в смысле надежности. Последовательные и параллельные соединения элементов считаются простейшими структурами, легко заменяемыми одним эквивалентным элементом с соответствующей функцией распределения состояний элементов в групп
|
|
|
