 |
Тогда средняя ошибка аппроксимации равна
|
|
|
|
Таблица 3.1 – Исходные данные
| Область | Средний размер назначенных ежемесячных пенсий, у.д.е., у | Прожиточный минимум в среднем на одного пенсионера в месяц, у.д.е., х |
| Орловская | ||
| Рязанская | ||
| Смоленская | ||
| Тверская | ||
| Тульская | ||
| Ярославская |
Эмпирические коэффициенты регрессии b0, b1 будем определять с помощью инструмента «Регрессия» надстройки «Анализ данных» табличного процессораMS Excel.
Алгоритм определения коэффициентов состоит в следующем.
1. Вводимисходные данные в табличный процессор MS Excel.
2. Вызываемнадстройку Анализ данных(рисунок 2).
3.Выбираем инструмент анализа Регрессия(рисунок 3).
4. Заполняем соответствующие позиции окна Регрессия (рисунок 4).
5. Нажимаем кнопку ОК окна Регрессия и получаем протокол решения задачи (рисунок 5)
 |
Рисунок 2 – Активизация надстройки Анализ данных
 |
Рисунок 3 – Выбор инструмента Регрессия
 |
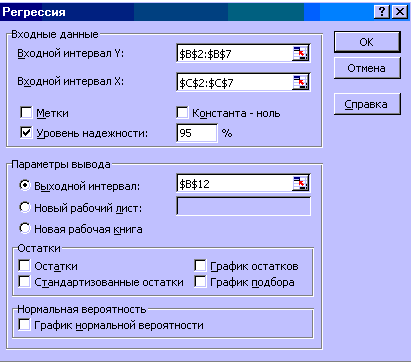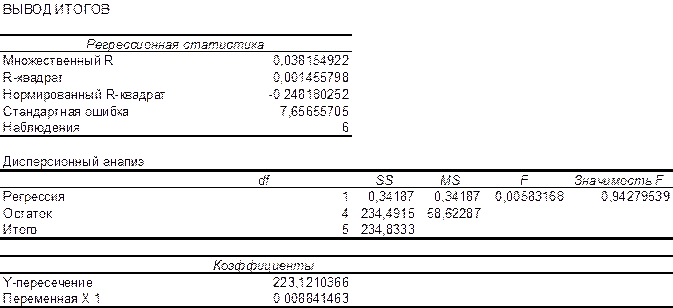
Рисунок 4 – Окно Регрессия
Рисунок 5 – Протокол решения задачи
Из рисунка 5 видно, что эмпирические коэффициенты регрессии соответственно равны
b0= 223,
b1 = 0, 0088.
Тогда уравнение парной линейной регрессии, связывающая величину ежемесячной пенсии у с величиной прожиточного минимумахимеет вид
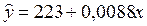.(3.2)
Далее, в соответствии с заданием необходимо оценить тесноту статистической связи между величиной прожиточного минимума х и величиной ежемесячной пенсии у. Эту оценку можно сделать с помощью коэффициента корреляции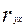 
. Величина этого коэффициента на рисунке 5 обозначена как множественный R и соответственно равна 0,038. Поскольку теоретически величина данного коэффициента находится в пределахот –1 до +1, то можно сделать вывод о не существенности статистической связимежду величиной прожиточного минимума х и величиной ежемесячной пенсии у.
|
|
|
Параметр «R – квадрат», представленныйна рисунке 5 представляет собой квадрат коэффициента корреляции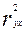 
и называется коэффициентом детерминации. Величина данного коэффициента характеризует долю дисперсии зависимой переменной у, объясненную регрессией (объясняющей переменной х). Соответственно величина 1- 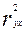характеризует долю дисперсии переменной у, вызванную влиянием всех остальных, неучтенных в эконометрической модели объясняющих переменных. Из рисунка 5 видно, что доля всех неучтенных в полученной эконометрической модели объясняющих переменных приблизительно составляет 1- 0,00145 = 0,998 или 99,8%.
На следующем этапе, в соответствии с заданием необходимо определить степень связи объясняющей переменной х с зависимой переменной у, используя коэффициент эластичности. Коэффициент эластичности для модели парной линейной регрессии определяется в виде:
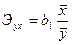. (3.3)
Тогда
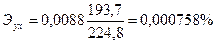
Следовательно, при изменении прожиточного минимума на 1% величина ежемесячной пенсии изменяется на 0,000758%.
Далее определяем среднюю ошибку аппроксимации по зависимости
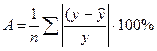. (3.4)
Для этого исходную таблицу 1 дополняем двумя колонками, в которых определяем значения,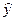 
рассчитанные с использованием зависимости (3.2) и значения разности 
.
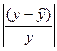Таблица 3.2. Расчет средней ошибки аппроксимации.
| Область | Средний размер назначенных ежемесячных пенсий, у.д.е., у | Прожиточный минимум в среднем на одного пенсионера в месяц, у.д.е., х |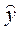 
| 
|
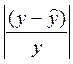
| Орловская | 0,032 | |||
| Рязанская | 0,045 | |||
| Смоленская | 0,021 | |||
| Тверская | 0,012 | |||
| Тульская | 0,028 | |||
| Ярославская | 0,017 | |||
| S=0,155 |
|
|
|
Тогда средняя ошибка аппроксимации равна
.
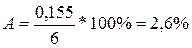Из практики известно, что значение средней ошибки аппроксимации не должно превышать (12…15)%
На последнем этапе выполним оценкустатистической надежности моделирования спомощью F – критерия Фишера. Для этого выполним проверку нулевой гипотезы Н0 о статистической не значимости полученного уравнения регрессиипо условию:
если при заданном уровне значимости a = 0,05 теоретическое (расчетное) значение F-критерия больше его критического значения Fкрит (табличного), то нулевая гипотеза отвергается, и полученное уравнение регрессии принимается значимым.
Из рисунка 5 следует, что Fрасч = 0,0058. Критическое значение F-критерия определяем с помощью использования статистической функции FРАСПОБР (рисунок 6). Входными параметрами функции является уровень значимости (вероятность) и число степеней свободы 1 и 2. Для модели парной регрессии число степеней свободы соответственно равно 1 (одна объясняющая переменная) и n-2 = 6-2=4.
 |
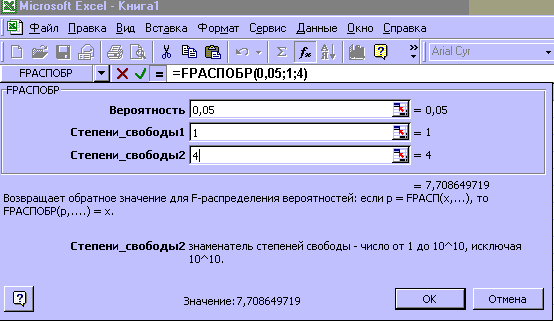Рисунок 6 – Окно статистической функции FРАСПОБР
Из рисунка 6 видно, что критическое значение F-критерия равно 7,71.
Так как Fрасч < Fкрит, то нулевая гипотеза не отвергается и полученное регрессионное уравнение статистически незначимо.
13. Построение модели множественной регрессии с использованием EXCEL.
В соответствии с вариантом задания, используя статистический материал, необходимо.
1. Построить линейное уравнение множественной регрессии пояснить экономический смысл его параметров.
2. Дать сравнительную оценку тесноты связи факторов с результативным признаком с помощью средних (общих) коэффициентов эластичности.
3. Оценить статистическую значимость коэффициентов регрессии с помощью t-критерия Стьюдента и нулевую гипотезу о значимости уравнения с помощью F-критерия.
4. Оценить качество уравнения посредством определения средней ошибки аппроксимации.
Исходные данные для построения модели парной регрессии приведены в таблице 3.3.
Таблица 3.3. Исходные данные.
| Чистый доход, млн. долларов США у | Оборот капитала, мл. долл. США, х1 | Использованный капитал, мл. долл. США, х2 |
| 6,6 | 6,9 | 83,6 |
| 2,7 | 93,6 | 25,4 |
| 1,6 | 10,0 | 6,4 |
| 2,4 | 31,5 | 12,5 |
| 3,3 | 36,7 | 14,3 |
| 1,8 | 13,8 | 6,5 |
| 2,4 | 64,8 | 22,7 |
| 1,6 | 30,4 | 15,8 |
| 1,4 | 12,1 | 9,3 |
| 0,9 | 31,3 | 18,9 |
|
|
|
Технология построения уравнения регрессии аналогична алгоритму, изложенному в пункте 3.1. Протокол построения уравнения регрессии показан на рисунке 7.
| ВЫВОД ИТОГОВ | |||
| Регрессионная статистика | |||
| Множественный R | 0,901759207 | ||
| R-квадрат | 0,813169667 | ||
| Нормированный R-квадрат | 0,759789572 | ||
| Стандартная ошибка | 0,789962026 | ||
| Наблюдения | |||
| Дисперсионный анализ | |||
| df | MS | F | |
| Регрессия | 9,50635999 | 15,23357468 | |
| Остаток | 0,624040003 | ||
| Итого | |||
| Коэффициенты | t-статистика | ||
| Y-пересечение | 1,113140304 | 2,270238114 | |
| Переменная X1 | -0,000592199 | -0,061275574 | |
| Переменная X2 | 0,063902851 | 5,496523193 |
Рисунок 7. Вывод итогов.
|
|
|
