| №п/п
| Задания
| Ответы
|
| Раздел: ЛИНЕЙНАЯ АЛГЕБРА.
|
| Тема 1.1: Определители-1.Определители второго, третьего и четвёртого порядков, миноры и алгебраические дополнения элементов.
|
| 1.
| Определитель  равен… Записать ответ. равен… Записать ответ.
| -5
|
| 2.
| Дан определитель  . Тогда минор . Тогда минор 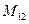 элемента элемента  равен…
Записать ответ. равен…
Записать ответ.
| -3
|
| 3.
| Дан определитель  . Тогда алгебраическое дополнение . Тогда алгебраическое дополнение  элемента элемента  равно… Записать ответ. равно… Записать ответ.
| -17
|
| 4.
| Определитель  равен:
1) равен:
1)  2) 2)  3) 3)  4) 4)  5) 5) 
| 2)
|
| 5.
| Определитель  равен… равен…
|
|
| 6.
| Дан определитель  . Указать все пары, соответствующих друг другу элементов . Указать все пары, соответствующих друг другу элементов  определителя и их алгебраических дополнений определителя и их алгебраических дополнений  : :
   
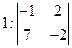   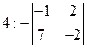 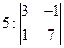 
| 1-2
2-4
3-6
4-3
|
|
| Если определитель  равен равен  , то определитель , то определитель  равен… равен…
|
|
| Тема 1.2: Определители-2.Вычисление определителей четвёртого порядка. Ранг матрицы и его вычисление.
|
| 1.
| Определитель  равен… равен…
|
|
| 2.
| Определитель 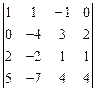 равен…
1) равен…
1)  2) 2)  3) 3)  4) 4)  5) 5) 
| 2) 
|
| 3.
| Ранг матрицы 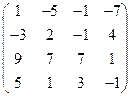 равен равен  1)
1)  2) 2)  3) 3)  4) 4)  5) 5) 
| 3) 
|
| Тема 1.3: Матрицы-1.Операции над матрицами (сложение, вычитание, умножение на число, умножение на матрицу, транспонирование). Вычисление определителя матрицы 2-го порядка.
|
| 1.
| Матрица С=АВ+2АТ, где  , ,  , имеет вид , имеет вид 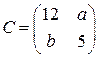 , где , где  , ,  . Ответ записать в виде: . Ответ записать в виде: 
| 
|
| 2.
| Если  , ,  , то матрица , то матрица  равна……
1) равна……
1)   2) 2)  3) 3)  4) 4)  5) 5) 
| 2)
|
| 3.
| Пусть  , где , где  , ,  . Тогда определитель . Тогда определитель  матрицы С равен… матрицы С равен…
| 
|
| Тема 1.4: Матрицы-2.Операции над матрицами (сложение, вычитание, умножение на число, умножение на матрицу, транспонирование). Нахождение обратной к матрице 3-го порядка.
|
| 1.
| Матрица  имеет вид имеет вид  , где , где  , , 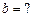 , , 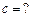 Ответ записать в виде: Ответ записать в виде: 
|

|
| 2.
| Матрица 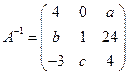 , является обратной к матрице , является обратной к матрице  . Тогда . Тогда  , , 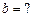 , , 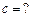 Ответ записать в виде: Ответ записать в виде: 
| -5,-18,0
|
| Тема 1.5: СЛАУ-1.Системы линейных алгебраических уравнений, методы их решения (методы Крамера и Гаусса).
|
| 1.
| Пусть  - решение системы линейных уравнений - решение системы линейных уравнений  , найденное по формулам Крамера. Тогда , найденное по формулам Крамера. Тогда   , где , где  ( ( целое число).
Ответ записать в виде: целое число).
Ответ записать в виде: 
|
|
| 2.
| Набор  значений неизвестных значений неизвестных  является решением невырожденной системы уравнений является решением невырожденной системы уравнений  ,если ,если  , , 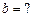 , , 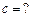 Ответ записать в виде:
Ответ записать в виде: 
| 
|
| Тема 1.6: СЛАУ-2.Координаты вектора в произвольном базисе, их вычисление. Матричные уравнения, их решение методом обратной матрицы.
|
| 1.
| Решением матричного уравнения  является матрица является матрица  , где , где  , ,  , ,  .
Ответ записать в виде: .
Ответ записать в виде: 
| 3,0,-2
|
| 2.
| Решением матричного уравнения  является матрица является матрица  , где , где  , ,  .
Ответ записать в виде: .
Ответ записать в виде: 
| 20,-8
|
| 3.
| Вектор 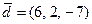 в произвольном базисе в произвольном базисе  , где , где  , , 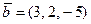 , ,  , имеет координаты , имеет координаты  , где , где  , ,  , ,  Ответ записать в виде
Ответ записать в виде  . .
| 1,1,1
|
| Тема 1.7: Алгебра (теория-1). Простейшие задачи и теоретические вопросы (в объёме вопросов к экзамену), в том числе: определители и их свойства; правило треугольников для определителя 3-его порядка; обратная матрица, условие её существования и нахождение; условие согласованности матриц для умножения; размерность произведения матриц; системы линейных уравнений, условия их совместности и несовместности, определенности и неопределённости; расширенная матрица системы.
|
| Тема 1.8: Алгебра (теория-2). Простейшие задачи и теоретические вопросы (в объёме вопросов к экзамену), в том числе: определители и их свойства; обратная матрица, условие её существования и нахождение; системы линейных уравнений, условия их совместности и несовместности (по теореме Кронекера-Капелли), определенности и неопределённости; линейно зависимые, линейно независимые, ортогональные системы векторов, их свойства; зависимость и независимость ортогональных систем векторов; ранг матрицы и его свойства; собственные числа и векторы матрицы, характеристическое уравнение, матрица квадратичной формы.
|
| Тема 1.9: Алгебра-3 (задачи).Координаты вектора в ортогональном базисе. Ортогональная составляющая. Собственные числа. Действия над линейными операторами. Квадратичные формы.
|
|
| Вектор  в ортогональном базисе в ортогональном базисе  , где , где   , ,  , имеет координаты , имеет координаты  , где , где 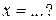 , , 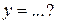 , ,  Ответ записать в виде: Ответ записать в виде: 
| 1/3,-1/2,-17/6
|
|
| Ортогональной составляющей вектора  относительно ортогональной системы векторов относительно ортогональной системы векторов 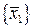 , где , где  является вектор является вектор  , где , где  , ,  , ,  Ответ записать в виде:
Ответ записать в виде: 
| -2/3,-2/3,-1/3
|
|
| Матрица линейного оператора  , где , где  , ,  , ,  , имеет вид , имеет вид  , где , где  , ,  Ответ записать в виде: Ответ записать в виде: 
| 0,-3
|
|
| Собственными числами матрицы  являются числа:
1) являются числа:
1)  2) 2)  3) 3) 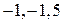 4) 4)  5) 5) 
| 3)
|
|
| Невырожденная квадратичная форма  будет (по критерию Сильвестра) положительно определённой при значениях параметра будет (по критерию Сильвестра) положительно определённой при значениях параметра  , принадлежащих промежутку , принадлежащих промежутку  , где , где  Ответ записать в виде:
Ответ записать в виде: 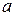
| 14/19
|
| Раздел: ВЕКТОРНАЯ АЛГЕБРА.
|
| Тема 2.1: Векторы-1.Координаты вектора, его длина. Деление отрезка пополам. Расстояние между точками. Проекция вектора на вектор. Скалярное произведение. Угол между векторами (косинус). Векторное произведение. Площадь треугольника и параллелограмма, объём пирамиды (с выбором ответа).
|
|
| Для векторов  , ,  модуль векторного произведения модуль векторного произведения  равен равен  , где , где  ( (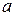 - целое число).
Ответ введите в виде: - целое число).
Ответ введите в виде: 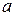
|
|
|
| Площадь треугольника, построенного на векторах  и и  равна… равна…
|
|
|
| Объём треугольной пирамиды  , построенной на векторах , построенной на векторах  , ,  и и  как на рёбрах, равен… как на рёбрах, равен…
|
|
| Тема 2.2: Векторы-2.Длина вектора. Угол между векторами (синус). Векторное произведение, его модуль. Принадлежность четырёх точек одной плоскости. Площадь треугольника и параллелограмма, объём тетраэдра.
|
| 1.
| Четыре точки  , ,  , ,  , ,  будут лежать в одной плоскости при значении параметра будут лежать в одной плоскости при значении параметра  равном…Записать ответ. равном…Записать ответ.
|
|
|
| Если  , ,  , ,  , то площадь треугольника, построенного на векторах , то площадь треугольника, построенного на векторах  и и 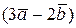 как на сторонах, равна…
Записать ответ. как на сторонах, равна…
Записать ответ.
|
|
|
| Площадь параллелограмма  с вершинами в точках с вершинами в точках  , ,  , ,  , ,  равна равна  , где , где  ( (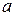 - целое число).
Ответ введите в виде: - целое число).
Ответ введите в виде: 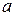
|
|
| Тема 2.3: Векторы (теория-1). Простейшие задачи.Условия компланарности, коллинеарности, ортогональности (перпендикулярности) векторов, равенство векторов. Скалярное произведение, его вычисление.
|
| 1.
| Векторы  , ,  и и  будут компланарными, если параметр будут компланарными, если параметр  равен… равен…
| 
|
| 2.
| Ортогональными из векторов  , ,  и и  являются:
1) являются:
1)  2) 2)  3) 3)  4) все 5) ортогональных нет 4) все 5) ортогональных нет
| 1)
|
| 3.
| Равными из векторов  , ,  и и  , где , где  , , 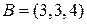 являются:
1) являются:
1)  2) 2)  3) 3)  4) все 5) равных нет 4) все 5) равных нет
| 5)
|
| 4.
| Среди векторов  , ,  и и  коллинеарны:
1) коллинеарны:
1)  2) 2)  3) 3)  4) все 5) нет коллинеарных 4) все 5) нет коллинеарных
| 4)
|
| 5.
| Из векторов  и и 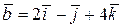 коллинеарны вектору коллинеарны вектору  , где , где  , ,  :
1) :
1)  2) 2)  3) 3)  4) 4) 
| 1)
|
| 6.
| Векторы  и и  будут параллельными друг другу при значениях параметров будут параллельными друг другу при значениях параметров  , ,  ( ( - целые числа).
Ответ введите в виде: - целые числа).
Ответ введите в виде: 
| 6,3
|
|
| Векторы  и и  взаимно перпендикулярны. Тогда параметр взаимно перпендикулярны. Тогда параметр  равен… равен…
|
|
|
| Векторным произведением векторов 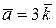 и и  является вектор является вектор  , где , где  , ,  ( (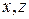 - целые числа). Ответ введите в виде: - целые числа). Ответ введите в виде: 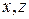
| 3,0
|
| Тема 2.4: Векторы (теория-2). Простейшие задачи векторной алгебры:координаты точки, делящей отрезок пополам; длина вектора, через координаты концов; вычисление расстояния между двумя точками; действия над векторами в координатной форме, в графическом виде; вычисление скалярного произведения; вычисление векторного произведения в координатной форме; нахождение орта вектора; условие коллинеарности векторов в координатной форме.
|
|
| В пространстве имеется отрезок, соединяющий две точки с аппликатами одинаковых знаков. Тогда этот отрезок не может пересекать:
1) плоскость  2)ось аппликат 2)ось аппликат  3)ось ординат 3)ось ординат  4)плоскость 4)плоскость 
| 1) 3)
|
| Тема 2.5: Векторы-3 (задачи).Нахождение координат вектора по заданным условиям (коллинеарности, ортогональности). Скалярное, векторное, смешанное произведения и их приложения.
|
| Раздел: АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ.
|
Тема 3.1. Прямая-1.Прямая на плоскости (различные формы записи уравнения прямой на плоскости: проходящей через точку перпендикулярно вектору, параллельно вектору, параллельно оси координат, через две точки, с угловым коэффициентом, в отрезках; угол между прямыми; точка пересечения прямых; расстояние от точки до прямой на плоскости; условия  и и  прямых, условие совпадения прямых, угловой коэффициент прямой, расстояние между двумя параллельными прямыми). прямых, условие совпадения прямых, угловой коэффициент прямой, расстояние между двумя параллельными прямыми).
|
|
| Расстояние между параллельными прямыми  и и  равно:
1) равно:
1) 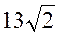 2) 2)  3) 3)  4) 4)  5) 5) 
| 5)
|
Тема 3.2. Прямая-2.Прямая на плоскости (различные формы записи уравнения прямой на плоскости: проходящей через точку перпендикулярно вектору, параллельно вектору, параллельно оси координат, через две точки, с угловым коэффициентом, в отрезках; угол между прямыми; точка пересечения прямых; расстояние от точки до прямой на плоскости; условия  и и  прямых, условие совпадения прямых, угловой коэффициент прямой, расстояние между двумя параллельными прямыми). прямых, условие совпадения прямых, угловой коэффициент прямой, расстояние между двумя параллельными прямыми).
|
| 1.
| Даны вершины треугольника  : : 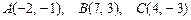 . Тогда уравнение медианы . Тогда уравнение медианы 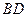 , проведённой из вершины , проведённой из вершины  , имеет вид: , имеет вид:  , где , где  , ,  ( ( -целые числа). Ответ записать в виде: -целые числа). Ответ записать в виде: 
|  , , 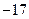
|
Тема 3.3. Плоскость-1. Плоскость (различные формы записи уравнения плоскости: проходящей через точку перпендикулярно вектору, через три точки, в отрезках; угол между плоскостями; расстояние от точки до плоскости; условия  и и  плоскостей). плоскостей).
|
| 1.
| Уравнение плоскости, проходящей через точку  параллельно плоскости параллельно плоскости  , имеет вид , имеет вид  , где , где  , ,  Ответ записать в виде: Ответ записать в виде: 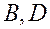
| 1,3
|
|
| Уравнение плоскости, проходящей через три точки:  , ,  , ,  имеет вид имеет вид  , где , где  , ,  , ( , ( - целые числа). Ответ введите в виде: - целые числа). Ответ введите в виде: 
| 1,0
|
Тема 3.4. Плоскость-2.Плоскость и прямая в пространстве (различные формы записи уравнения плоскости: проходящей через точку перпендикулярно вектору, через три точки, в отрезках; угол между плоскостями; расстояние от точки до плоскости; условия  и и  плоскостей; различные формы записи уравнения прямой в пространстве: проходящей через две точки, параметрическое; угол между прямыми, прямой и плоскостью; условия плоскостей; различные формы записи уравнения прямой в пространстве: проходящей через две точки, параметрическое; угол между прямыми, прямой и плоскостью; условия  и и  прямой и плоскости; точка пересечения прямой и плоскости). прямой и плоскости; точка пересечения прямой и плоскости).
|
| 1.
| Плоскость  будет перпендикулярна прямой будет перпендикулярна прямой   при значении параметра при значении параметра  Записать ответ. Записать ответ.
| 
|
| 2.
| Даны вершины пирамиды  : :  . Тогда расстояние от вершины . Тогда расстояние от вершины  до плоскости до плоскости 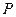 , проходящей через точку , проходящей через точку  перпендикулярно вектору перпендикулярно вектору  , равно , равно  , где , где  ( ( - целое число).
Ответ записать в виде: - целое число).
Ответ записать в виде: 
| 
|
| Тема 3.5. Кривая-1. Классификация кривых второго порядка. Нахождение вершины параболы, центра и радиуса окружности, центров эллипса и гиперболы.
|
| 1.
| Уравнение  определяет…..
1)окружность 2)эллипс 3)гиперболу5)параболу определяет…..
1)окружность 2)эллипс 3)гиперболу5)параболу
| 1)
|
| 2.
| Уравнение  определяет:
1)эллипс 2) гиперболу 3) параболу определяет:
1)эллипс 2) гиперболу 3) параболу
| 3)
|
| 3.
| Точка  является вершиной параболы является вершиной параболы  . Тогда координаты . Тогда координаты  точки точки  равны…
Ответ записать в виде: равны…
Ответ записать в виде: 
| 1,3
|
|
| Уравнение окружности с центром в точке  , которая проходит через начало координат, имеет вид , которая проходит через начало координат, имеет вид  , где радиус , где радиус  окружности равен… окружности равен…
|
|
| 5.
| Точка  является центром эллипса является центром эллипса  . Тогда координаты . Тогда координаты  точки точки  равны… Ответ записать в виде: равны… Ответ записать в виде: 
| 3,-1
|
| Тема 3.6. Кривая-2.Расстояние между центрами окружностей. Нормальное уравнение окружности. Канонические уравнения эллипсов и гиперболы, нахождение их фокусов и эксцентриситетов.
|
| Тема 3.7. Геометрия (теория-1). Простейшие задачи и теоретические вопросы (в объёме вопросов к экзамену), в том числе: различные формы записи уравнений прямой на плоскости и плоскости; взаимное расположение прямых на плоскости и плоскостей (параллельность, перпендикулярность, пересечение, совпадение); угловой коэффициент прямой; расстояние от точки до прямой на плоскости; расстояние от точки до плоскости.
|
|
| Даны графики прямых  : :
 Угловой коэффициент прямой
Угловой коэффициент прямой 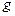 равен:
1) равен:
1)  2) 2)  3) 3)  4) 4)  5) 5) 
| 5)
|
| Тема 3.8. Геометрия (теория-2). Простейшие задачи и теоретические вопросы (в объёме вопросов к экзамену), в том числе: различные формы записи уравнений плоскости, прямой на плоскости и в пространстве; взаимное расположение прямых и плоскостей (параллельность, перпендикулярность, пересечение, совпадение); нормальные уравнения сферы и окружности; расстояние от точки до прямой на плоскости; расстояние от точки до плоскости; соответствие между кривыми второго порядка и их уравнениями; канонические уравнения эллипса, гиперболы, параболы; полуоси эллипса и гиперболы; радиус и центр окружности; определения эллипса, гиперболы и параболы, как геометрических мест точек на плоскости.
|
| Раздел: КОМПЛЕКСНЫЕ ЧИСЛА.
|
| Тема 4.1 Комплексные числа.Сложение, вычитание, умножение, деление, возведение в целую степень комплексных чисел. Комплексно-сопряжённое число. Действительная и мнимая части комплексного числа или выражения.
|
|
| Комплексное число  записано в виде записано в виде  . Тогда его действительная часть . Тогда его действительная часть  равна равна  , где , где 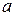 - целое число, равное…
Записать ответ. - целое число, равное…
Записать ответ.
|
|
|
| Комплексное число  записано в виде записано в виде  . Тогда его мнимая часть . Тогда его мнимая часть  равна равна  , где , где 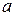 - целое число, равное… Записать ответ. - целое число, равное… Записать ответ.
|
|
|
| Корни квадратного уравнения  на множестве комплексных чисел имеют вид на множестве комплексных чисел имеют вид  , где , где 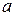 - целое число, равное… Записать ответ. - целое число, равное… Записать ответ.
| -1
|

 равен… Записать ответ.
равен… Записать ответ.
 . Тогда минор
. Тогда минор 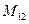 элемента
элемента  равен…
Записать ответ.
равен…
Записать ответ.
 . Тогда алгебраическое дополнение
. Тогда алгебраическое дополнение  элемента
элемента  равно… Записать ответ.
равно… Записать ответ.
 равен:
1)
равен:
1)  2)
2)  3)
3)  4)
4)  5)
5) 
 равен…
равен…
 . Указать все пары, соответствующих друг другу элементов
. Указать все пары, соответствующих друг другу элементов  определителя и их алгебраических дополнений
определителя и их алгебраических дополнений  :
:




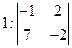


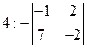
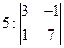

 равен
равен  , то определитель
, то определитель  равен…
равен…
 равен…
равен…
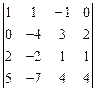 равен…
1)
равен…
1)  2)
2)  3)
3)  4)
4)  5)
5) 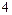

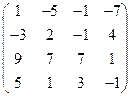 равен
равен  1)
1)  2)
2)  3)
3) 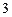 4)
4)  5)
5) 
 ,
,  , имеет вид
, имеет вид 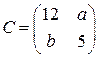 , где
, где  ,
,  . Ответ записать в виде:
. Ответ записать в виде: 

 ,
,  , то матрица
, то матрица  равна……
1)
равна……
1) 
 2)
2)  3)
3)  4)
4)  5)
5) 
 , где
, где  ,
,  . Тогда определитель
. Тогда определитель  матрицы С равен…
матрицы С равен…

 имеет вид
имеет вид  , где
, где  ,
, 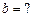 ,
, 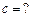 Ответ записать в виде:
Ответ записать в виде: 

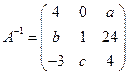 , является обратной к матрице
, является обратной к матрице  . Тогда
. Тогда  ,
, 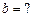 ,
, 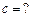 Ответ записать в виде:
Ответ записать в виде: 
 - решение системы линейных уравнений
- решение системы линейных уравнений  , найденное по формулам Крамера. Тогда
, найденное по формулам Крамера. Тогда 
 , где
, где  (
( целое число).
Ответ записать в виде:
целое число).
Ответ записать в виде: 
 значений неизвестных
значений неизвестных  является решением невырожденной системы уравнений
является решением невырожденной системы уравнений  ,если
,если  ,
, 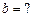 ,
, 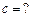 Ответ записать в виде:
Ответ записать в виде: 

 является матрица
является матрица  , где
, где  ,
,  ,
,  .
Ответ записать в виде:
.
Ответ записать в виде: 
 является матрица
является матрица  , где
, где  ,
,  .
Ответ записать в виде:
.
Ответ записать в виде: 
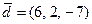 в произвольном базисе
в произвольном базисе  , где
, где  ,
, 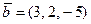 ,
,  , имеет координаты
, имеет координаты  , где
, где  ,
,  ,
,  Ответ записать в виде
Ответ записать в виде  .
.
 в ортогональном базисе
в ортогональном базисе  , где
, где 
 ,
,  , имеет координаты
, имеет координаты  , где
, где 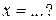 ,
, 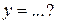 ,
,  Ответ записать в виде:
Ответ записать в виде: 
 относительно ортогональной системы векторов
относительно ортогональной системы векторов 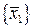 , где
, где  является вектор
является вектор  , где
, где  ,
,  ,
,  Ответ записать в виде:
Ответ записать в виде: 
 , где
, где  ,
,  ,
,  , имеет вид
, имеет вид  , где
, где  ,
,  Ответ записать в виде:
Ответ записать в виде: 
 являются числа:
1)
являются числа:
1)  2)
2)  3)
3) 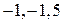 4)
4)  5)
5) 
 будет (по критерию Сильвестра) положительно определённой при значениях параметра
будет (по критерию Сильвестра) положительно определённой при значениях параметра  , принадлежащих промежутку
, принадлежащих промежутку  , где
, где  Ответ записать в виде:
Ответ записать в виде: 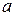
 ,
,  модуль векторного произведения
модуль векторного произведения  равен
равен  , где
, где  (
(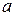 - целое число).
Ответ введите в виде:
- целое число).
Ответ введите в виде: 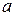
 и
и  равна…
равна…
 , построенной на векторах
, построенной на векторах  ,
,  и
и  как на рёбрах, равен…
как на рёбрах, равен…
 ,
,  ,
,  ,
,  будут лежать в одной плоскости при значении параметра
будут лежать в одной плоскости при значении параметра  равном…Записать ответ.
равном…Записать ответ.
 ,
,  ,
,  , то площадь треугольника, построенного на векторах
, то площадь треугольника, построенного на векторах  и
и 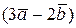 как на сторонах, равна…
Записать ответ.
как на сторонах, равна…
Записать ответ.
 с вершинами в точках
с вершинами в точках  ,
,  ,
,  ,
,  равна
равна  , где
, где  (
(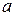 - целое число).
Ответ введите в виде:
- целое число).
Ответ введите в виде: 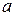
 ,
,  и
и  будут компланарными, если параметр
будут компланарными, если параметр  равен…
равен…

 ,
,  и
и  являются:
1)
являются:
1)  2)
2)  3)
3)  4) все 5) ортогональных нет
4) все 5) ортогональных нет
 ,
,  и
и  , где
, где  ,
, 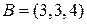 являются:
1)
являются:
1)  2)
2)  3)
3)  4) все 5) равных нет
4) все 5) равных нет
 ,
,  и
и  коллинеарны:
1)
коллинеарны:
1)  2)
2)  3)
3)  4) все 5) нет коллинеарных
4) все 5) нет коллинеарных
 и
и 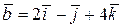 коллинеарны вектору
коллинеарны вектору  , где
, где  ,
,  :
1)
:
1)  2)
2)  3)
3)  4)
4) 
 и
и  будут параллельными друг другу при значениях параметров
будут параллельными друг другу при значениях параметров  ,
,  (
( - целые числа).
Ответ введите в виде:
- целые числа).
Ответ введите в виде: 
 и
и  взаимно перпендикулярны. Тогда параметр
взаимно перпендикулярны. Тогда параметр  равен…
равен…
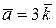 и
и  является вектор
является вектор  , где
, где  ,
,  (
(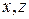 - целые числа). Ответ введите в виде:
- целые числа). Ответ введите в виде: 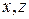
 2)ось аппликат
2)ось аппликат  3)ось ординат
3)ось ординат  4)плоскость
4)плоскость 
 и
и  прямых, условие совпадения прямых, угловой коэффициент прямой, расстояние между двумя параллельными прямыми).
прямых, условие совпадения прямых, угловой коэффициент прямой, расстояние между двумя параллельными прямыми).
 и
и  равно:
1)
равно:
1) 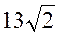 2)
2)  3)
3)  4)
4)  5)
5) 
 и
и  прямых, условие совпадения прямых, угловой коэффициент прямой, расстояние между двумя параллельными прямыми).
прямых, условие совпадения прямых, угловой коэффициент прямой, расстояние между двумя параллельными прямыми).
 :
: 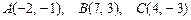 . Тогда уравнение медианы
. Тогда уравнение медианы 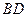 , проведённой из вершины
, проведённой из вершины  , имеет вид:
, имеет вид:  , где
, где  ,
,  (
( -целые числа). Ответ записать в виде:
-целые числа). Ответ записать в виде: 
 ,
, 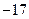
 и
и  плоскостей).
плоскостей).
 параллельно плоскости
параллельно плоскости  , имеет вид
, имеет вид  , где
, где  ,
,  Ответ записать в виде:
Ответ записать в виде: 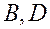
 ,
,  ,
,  имеет вид
имеет вид  , где
, где  ,
,  , (
, ( - целые числа). Ответ введите в виде:
- целые числа). Ответ введите в виде: 
 и
и  плоскостей; различные формы записи уравнения прямой в пространстве: проходящей через две точки, параметрическое; угол между прямыми, прямой и плоскостью; условия
плоскостей; различные формы записи уравнения прямой в пространстве: проходящей через две точки, параметрическое; угол между прямыми, прямой и плоскостью; условия  и
и  прямой и плоскости; точка пересечения прямой и плоскости).
прямой и плоскости; точка пересечения прямой и плоскости).
 будет перпендикулярна прямой
будет перпендикулярна прямой 
 при значении параметра
при значении параметра  Записать ответ.
Записать ответ.

 :
:  . Тогда расстояние от вершины
. Тогда расстояние от вершины  до плоскости
до плоскости 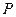 , проходящей через точку
, проходящей через точку  перпендикулярно вектору
перпендикулярно вектору  , равно
, равно  , где
, где  (
( - целое число).
Ответ записать в виде:
- целое число).
Ответ записать в виде: 

 определяет…..
1)окружность 2)эллипс 3)гиперболу5)параболу
определяет…..
1)окружность 2)эллипс 3)гиперболу5)параболу
 определяет:
1)эллипс 2) гиперболу 3) параболу
определяет:
1)эллипс 2) гиперболу 3) параболу
 является вершиной параболы
является вершиной параболы  . Тогда координаты
. Тогда координаты  точки
точки  равны…
Ответ записать в виде:
равны…
Ответ записать в виде: 
 , которая проходит через начало координат, имеет вид
, которая проходит через начало координат, имеет вид  , где радиус
, где радиус  окружности равен…
окружности равен…
 является центром эллипса
является центром эллипса  . Тогда координаты
. Тогда координаты  точки
точки  равны… Ответ записать в виде:
равны… Ответ записать в виде: 
 :
:
 Угловой коэффициент прямой
Угловой коэффициент прямой 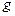 равен:
1)
равен:
1)  2)
2)  3)
3)  4)
4)  5)
5) 
 записано в виде
записано в виде  . Тогда его действительная часть
. Тогда его действительная часть  равна
равна  , где
, где 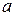 - целое число, равное…
Записать ответ.
- целое число, равное…
Записать ответ.
 записано в виде
записано в виде  . Тогда его мнимая часть
. Тогда его мнимая часть  равна
равна  , где
, где 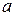 - целое число, равное… Записать ответ.
- целое число, равное… Записать ответ.
 на множестве комплексных чисел имеют вид
на множестве комплексных чисел имеют вид  , где
, где 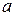 - целое число, равное… Записать ответ.
- целое число, равное… Записать ответ.


