 |
Динамика поступательного движения
|
|
|
|
КИНЕМАТИКА
Материальная точка движется по окружности радиуса r. Движение точки можно описывать либо как поступательное по криволинейной траектории, либо как поворот соответствующего радиуса-вектора. Поэтому дана либо временная зависимость координаты точки S (t) (варианты 1–12, 26), либо зависимость угла поворота радиуса-вектора от времени φ(t) (варианты 13–25). Точка начинает двигаться при t = 0. Требуется проанализировать ее движение на заданном интервале времени (0 ≤ t ≤ 6 с в вариантах 1 – 12, 26 и 0 ≤ t ≤ 1 с в вариантах 13–25).
Кроме того, следует определить в указанный момент времени t 1:
1) линейную 
и угловую 
скорости (т. е. направление и величины);
2) путь S 1, пройденный точкой с момента начала движения;
3) нормальное 
, тангенциальное 
и полное 
ускорения, а также угловое ускорение 
точки.
Исходные данные приведены в табл. 1.1.
Рассмотрим в качестве примера 26-й вариант.
Для краткости опустим словесную формулировку задачи.
Решение
Чтобы понять, как движется точка при 0 ≤ t ≤ 6 с, построим графики зависимостей S (t) и υ (t) = 
(t) на этом временном интервале:
υ (t) = 2 t – 4.
Выберем в качестве начала отсчета на окружности точку А (рис. 1.1). Положительные значения S и φ будем откладывать против, отрицательные – по ходу часовой стрелки. При t = 0 имеем S = 3 м, что соответствует, скажем, точке В. В течение 
первой секунды движения величина S уменьшается до нуля, т. е. точка попадает из В в А, двигаясь по ходу часовой стрелки. Скорость при этом отрицательна. В течение второй секунды точка продолжает двигаться в том же направлении и при t = 2 с попадает в С, где S = – 1 м. Скорость в этот момент равна нулю. В течение третьей секунды точка движется из С против хода часовой стрелки (υ (t) > 0 при 2 с < t ≤ 3 с) и при t = 3 с попадает в А (S = 0). При t > 3 с, как видно из графиков, S (t) > 0 и υ (t) > 0. Следовательно, точка будет далее двигаться против хода часовой стрелки. Отметим, что а (t) =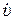 
(t) = 2 м/с2, т. е. движение точки равноускоренное.
|
|
|
Определение величин пути, скоростей и ускорений производится по стандартным формулам и здесь не приводится. Зная направление движения точки (против хода часовой стрелки), также легко определить направление линейной и угловой скоростей при t 1 = 4 с.
Таблица 1.1
| № вар. | Уравнение движения | t 1, с | r, м | |
| S (t), м | φ(t), рад | |||
| S = – t 2 + 5 t – 4 | ||||
| S = t 3 – 3 t 2 + 2 t | ||||
| S = t 2 – 6 t + 8 | ||||
| S = – 10 + 7 t – t 2 | ||||
| S = – t 3 + 4 t 2 – 3 t | ||||
| S = t 2 – 3 t + 2 | ||||
| S = – 12 t + 7 t 2 – t 3 | ||||
| S = t 3 – 6 t 2 + 8 t | ||||
| S = 6 – 5 t + t 2 | ||||
| S = – t 2 + 6 t – 5 | ||||
| S = – 6 t + 5 t 2 – t 3 | ||||
| S = – 7 t + 12 + t 2 |
Окончание табл. 1.1
| № вар. | Уравнение движения | t 1, с | r, м | |
| S (t), м | φ(t), рад | |||
| φ = t 2 – 0,8 t + 0,15 | 0,4 | |||
| φ = 0,02 t – 0,3 t 2 + t 3 | 0,5 | |||
| φ = t 2 – 0,4 t + 0,03 | 0,2 | |||
| φ = 0,06 t – 0,5 t 2 + t 3 | 0,4 | |||
| φ = –0,04 + 0,5 t – t 2 | 0,6 | |||
| φ = –0,7 t + t 2 + 0,12 | 0,8 | |||
| φ = t 2 – 0,6 t + 0,08 | 0,3 | |||
| φ = t 3 + 0,12 t – 0,7 t 2 | 0,7 | |||
| φ = t 2 + 5 t – 6 | 0,9 | |||
| φ = t 3 – 0,7 t 2 + 0,1 t | 0,4 | |||
| φ = – t 3 + 0,4 t 2 – 0,03 t | 0,2 | |||
| φ = 0,02 – 0,3 t + t 2 | 0,6 | |||
| φ = – t 2 + 0,6 t – 0,05 | 0,4 | |||
| S = t 2 – 4 t + 3 |
ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ
Варианты 1–6, 26.
К грузу массой m 1 подвешен на веревке груз массой m 3. Масса веревки m 2. Вся система поднимается вертикально вверх под действием силы 
. Сила натяжения веревки со стороны груза m 1 равна 
, а со стороны груза m 3 равна 
.
|
|
|
Варианты 7–12.
Три тела, связанных невесомыми нитями, лежат на гладкой горизонтальной поверхности. К телу массой m 1 приложена сила , направленная вдоль поверхности, а к телу массой m 3 – сила 
, направленная в противоположную сторону. Ввиду невесомости нитей силы натяжения между телами m 1 и m 2 и между телами m 2 и m 3 можно считать постоянными по всей длине соответствующей нити. Трением пренебречь.
|
|
|
|
|
|
|
 |  |  |  | ||||||
 |
Варианты 13–19.
Маляр, масса которого m 1, работает в подвесном кресле. При подъеме вверх он тянет веревку с такой силой , что его сила давления на кресло уменьшается до . Масса кресла равна m 2 (рис. 2.1).
 | |||
 | |||
Варианты 20–25.
Невесомый блок укреплен в вершине наклонной плоскости, составляющей с горизонтом угол α. Гири с массами m 1 и m 2 соединены невесомой нитью и перекинуты через блок. Сила натяжения нити 
. Коэффициент трения гири с массой m 2 о наклонную плоскость равен k. Трением в блоке можно пренебречь (рис. 2.2).
Исходные данные для всех вариантов приведены в табл. 2.1.
Таблица 2.1
| № вар. | m 1, кг | m 2, кг | m 3, кг | F 1, H | F 2, H | Fнат 1, H | Fнат 2, H | а, м/с2 |
| 5 · 10-3 | ? | 3 · 10-3 | ? | - | 8 · 10-2 | 6 · 10-2 | ? | |
| 5 · 10-4 | ? | ? | ? | - | 3 · 10-2 | 25 · 10-3 | 6,7 | |
| ? | 10-3 | 5 · 10-3 | 12 · 10-2 | - | ? | 10 · 10-2 | ? | |
| 10-3 | ? | 15 · 10-4 | 5 · 10-2 | - | ? | ? | 6,7 | |
| 4 · 10-3 | 10-3 | ? | 13,5 · 10-2 | - | ? | ? | ||
| 3 · 10-2 | ? | 44 · 10-2 | - | ? | 11 · 10-2 | ? | ||
| 10-3 | 5 · 10-4 | 15 · 10-4 | 5 · 10-2 | - | ? | ? | ? |
Продолжение табл. 2.1
| № вар. | m 1, кг | m 2, кг | m 3, кг | F 1, H | F 2, H | Fнат 1, H | Fнат 2, H | а, м/с2 |
| 10-1 | 2 · 10-1 | 3 · 10-1 | ? | ? | ? | |||
| ? | ? | ? | 0,5 | 86 · 10-2 | 58 · 10-2 | 2,8 | ||
| 2 · 10-2 | 8 · 10-2 | ? | 1,8 | ? | ? | |||
| 5 · 10-1 | 10-1 | 8 · 10-1 | ? | ? | 2,29 | 2,14 | ? | |
| 10-1 | ? | 3 · 10-1 | ? | ? | 13,3 | |||
| ? | 10-1 | 3 · 10-2 | 0,5 | ? | 58 · 10-2 | ? | ||
| - | - | ? | - | ? | ||||
| - | ? | - | ? | - | ||||
| ? | ? | - | - | - | ||||
| - | ? | - | - | ? | ||||
| ? | - | - | ? | - | ||||
| ? | - | - | ? | - | ||||
| ? | - | - | - | ? |
Окончание табл. 2.1
| № вар. | m 1, кг | m 2, кг | Fнат, H | α, град | k | а, м/с2 |
| ? | 0,1 | ? | ||||
| ? | ? | 2,45 | ||||
| ? | ? | ? | 0,2 | |||
| ? | ? | |||||
| ? | ? | |||||
| ? | ? | 0,1 | 4,4 |
|
|
|
Здесь а – ускорение системы.
Рассмотрим, например, 26-й вариант задачи.
К грузу массой m 1 = 10-3 кг подвешен на веревке груз массой m 3 = 15 · 10-4 кг. Масса веревки m 2 = 5 · 10-4 кг. Вся система поднимается вертикально вверх с силой F 1 = 5 · 10-2 Н. Определить силы натяжения веревки и ускорение системы.
Решение
На груз m 1 действуют три силы: со стороны Земли – сила тяжести 
; со стороны растянутых нитей – сила натяжения и сила тяги . На груз m 3 действуют две силы: со стороны Земли – сила тяжести 
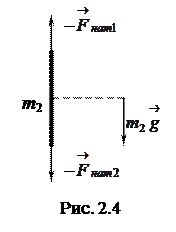
и со стороны нити – сила натяжения . На рис. 2.3 точки приложения сил выведены вправо от грузов. На веревку массой m 2 действуют три силы (рис. 2.4): со стороны Земли – сила тяжести 
; со стороны верхнего груза – сила, равная по величине и противоположная по направлению силе, с которой веревка действует на этот груз, т. е. (– ); со стороны нижнего груза – сила, равная (– ).
Проведенный анализ позволяет написать уравнение движения (второй закон Ньютона) в векторном виде для каждого из трех рассматриваемых тел в отдельности. Спроектировав эти уравнения на ось у (вдоль этой оси совершается движение тел), получим систему из трех алгебраических уравнений с постоянными коэффициентами, решение которой дает следующие результаты:
м/с2;
Н;
Н.
Анализ ответа. Если m 2 = 0, т. е. нить «невесома», то натяжение вдоль всей нити одинаково:
.
Примечание: в вариантах 7–12 ось удобно выбирать по горизонтали, а в вариантах 20–25 одну из осей – вдоль наклонной плоскости.
Сила трения (варианты 20–25) в данном случае определяется как произведение коэффициента трения на силу нормального давления (т. е. составляющую веса тела, перпендикулярную наклонной плоскости).
В вариантах 1–6 необходимо получить расчетные формулы для а, Fнат 1, Fнат 2.
Проверка правильности размерности результатов здесь достаточно проста, и для краткости ее опускаем.
РАБОТА
|
|
|
Варианты 1–8, 26.
Под действием постоянной силы тяги F вагонетка массой m прошла путь S за время t и приобрела скорость υ. Ускорение вагонетки а. Коэффициент трения k. Работа силы F по движению вагонетки равна А.
Варианты 9–16.
Груз массой m под действием постоянной силы F за время t поднимается на высоту h. Ускорение груза а. Скорость в конце подъема υ. Работа силы F по подъему груза равна А.
Варианты 17–25.
Груз массой m под действием постоянной силы тяги F поднимается по наклонной плоскости длиной l за время t. Ускорение груза а, скорость в конце подъема υ. Коэффициент трения k. Угол наклона плоскости φ. Работа силы F по подъему груза равна А.
Исходные данные для всех вариантов приведены в табл. 3.1–3.3.
Таблица 3.1
| № вар. | m, кг | υ, м/с | S, м | а, м/с2 | k | t, с | А, Дж | F, Н |
| 4 · 102 | ? | ? | 2 · 10-2 | ? | 103 | ? | ||
| 4,5 · 102 | ? | ? | ? | 10-2 | ? | 2 · 102 | ||
| ? | ? | 0,5 | 10-2 | ? | 103 | ? | ||
| ? | ? | ? | 0,4 | 2 · 10-2 | ? | 2,2 · 102 | ||
| 3 · 102 | ? | ? | ? | 9 · 102 | ? | |||
| 4 · 102 | ? | ? | 10-2 | ? | ? | |||
| 5 · 102 | ? | ? | 0,4 | ? | ? | 2,5 · 102 | ||
| 6 · 102 | ? | 0,2 | 3 · 10-2 | ? | ? | ? | ||
| 4 · 102 | ? | 10-2 | ? | ? | ? |
Таблица 3.2
| № вар. | m, кг | υ, м/с | h, м | t, с | F, Н | А, Дж | а, м/с2 |
| 102 | ? | ? | ? | ? | |||
| ? | ? | ? | 5 · 103 | ? | |||
| 1,5 · 102 | ? | ? | ? | ? | |||
| ? | ? | ? | ? | 2 · 103 | 4,8 · 103 | 2,1 | |
| 102 | ? | ? | 1,2 · 103 | ? | ? | ||
| ? | ? | ? | 6 · 103 | ? | |||
| 2 · 102 | ? | ? | 3 · 103 | ? | ? | ||
| 102 | ? | ? | ? | 1,5 · 103 | 5,5 · 103 | ? |
Таблица 3.3
| № вар. | m, кг | υ, м/с | l, м | t, с | а, м/с2 | φ, град | k | F, Н | А, Дж |
| 102 | ? | ? | 0,1 | ? | ? | ||||
| ? | ? | ? | 1,2 | 0,1 | 7 · 102 | ? | |||
| 1,2 · 102 | ? | ? | 2,1 | 0,9 | ? | ? | 2 · 103 | ||
| 0,9 · 102 | ? | 1,9 | ? | 0,1 | ? | ? | |||
| ? | 2,1 | ? | ? | 0,1 | ? | 1,4 · 103 | |||
| 102 | 1,9 | ? | ? | 1,1 | ? | 8 · 102 | ? | ||
| 2 · 102 | ? | 2,5 | ? | 0,1 | ? | ? | |||
| 0,8 · 102 | 1,8 | ? | ? | ? | 0,1 | 7 · 102 | ? | ||
| 102 | ? | ? | ? | 0,1 | ? | 1,4 · 103 |
Рассмотрим в качестве примера 26-й вариант.
Под действием постоянной силы F вагонетка массой 400 кг прошла путь 5 м и приобрела скорость 2 м/с. Коэффициент трения равен 0,01. Определить время t движения и ускорение а вагонетки, а также силу, действующую на вагонетку, и работу А этой силы.
Решение
Работа постоянной силы F по перемещению вагонетки равна
. (3.1)
Для определения силы F запишем уравнение движения (2-й закон Ньютона) для вагонетки (рис. 3.1)
+ 
= 
(3.2)
Сила трения Fтр равна по величине произведению коэффициента трения на силу нормального давления и в данном случае
. (3.3)
Равноускоренное движение вагонетки описывается соотношениями
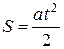; υ = аt. (3.4)
Решение системы уравнений (3.1)–(3.4) дает следующие результаты:
|
|
|
t = 5 c; a = 0,4 м/с2;
Н;
Дж.
Примечание. В результате воздействия внешней силы вагонетка преодолевает сопротивление силы трения и приобретает кинетическую энергию. Поэтому работу А можно определить также из следующего соотношения:
Дж.
Проверка размерностей результатов здесь достаточно проста, и для краткости ее опускаем.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Трофимова Т. И. Курс физики / Т. И. Трофимова. – М.: Высш. шк., 2000. – 542 с.
2. Савельев И. В. Курс общей физики: в 3 т. / И. В. Савельев. – М.: Наука, 1982. – Т. 1. – 432 с.
3. Чертов А. Г. Задачник по физике / А. Г. Чертов, А. А. Воробьев. – М.: Высш. шк., 1988. – 527 с.
|
|
|
