Порядок выполнения работы.

Шаг 0. Подготовительная работа.

Занесем статистические данные в электронную таблицу по столбцам (см. рис. 1.1).

Рис. 1.1. Таблица исходных данных

 

Шаг 1. Построить уравнение регрессии, описывающее зависимость между независимым и результативным фактором. Оценить качество уравнения регрессии, статистическую значимость его параметров и всего уравнения в целом.

Вызываем команду СЕРВИС – АНАЛИЗ ДАННЫХ – РЕГРЕССИЯ (см. рис. 1.2).

Рис. 1.2. Меню команды РЕГРЕССИЯ

 

В меню команды РЕГРЕССИЯ заполняем окошки. Входной интервал Y: вводим адреса ячеек, соответствующих значениям фактора y. Входной интервал X: адреса тех ячеек, которые соответствуют фактору x. Если адреса ячеек введены вместе с заглавием, то ставится птичка рядом со словом Метки. В этом случае верхние ячейки распознаются компьютером как названия и не участвуют в расчетах. Параметры вывода: необходимо указать, где именно компьютер должен вывести информацию. Выходной интервал: информация будет выведена на том же листе, в этом случае задается адрес левой верхней ячейки, с которой будет происходить вывод (см. рис. 1.2). Новый рабочий лист: нужно указать название листа. Новая рабочая книга: результаты будут выведены в новой рабочей книге. Также необходимо установить птички, в зависимости от того, какая дополнительная информация вам нужна. Далее нажимаем кнопку ОК. На экране появится протокол регрессионного анализа: три таблицы с расчетами (см. рис. 1.3). Если же была запрошена дополнительная информация, то количество таблиц увеличится. Например, следует также дополнительно изучить Остатки и График остатков. Описание содержащихся в протоколе данных см. в приложении 1.

Рис. 1.3. Протокол выполнения регрессионного анализа

 

Согласно результатам расчетов получено следующее уравнение регрессии:

Для оценки статистической значимости параметров и уравнения в целом рассчитаем t_кр и F_кр (см. приложение 2) и сравним их с расчетными значениями.

 

Шаг 2. Проверить остатки уравнения регрессии на гетероскедастичность.

Проверим выполнение одной из предпосылок метода наименьших квадратов – постоянство дисперсий остатков уравнения регрессии. График остатков (см. рис. 1.4) показывает, что остатки регрессии являются гомоскедастичными.

Рис. 1.4. График случайных составляющих регрессии

 

Проверим это предположение при помощи критерия Голдфелда – Квандта. Сначала упорядочим таблицу исходных данных по переменной x. Выделим курсором область B2:C14 (см. рис. 1.1). Вызовем меню ДАННЫЕ – СОРТИРОВКА – СОРТИРОВАТЬ ПО x – ОК. Исключим из рассмотрения d средних наблюдений (d должно быть примерно равно трети общего количества наблюдений). При помощи АНАЛИЗ ДАННЫХ – РЕГРЕССИЯ построим по первой и по третьей группе наблюдений регрессию (см. рис. 1.5). В ячейке С28 рассчитана сумма квадратов остатков регрессии по первой группе наблюдений , в ячейке I28 – по третьей группе наблюдений . Вычислим отношение большей остаточной суммы квадратов к меньшей. В нашем случае . Полученное отношение имеет F -распределение со степенями свободы и , где и – количество наблюдений в первой и третьей группе соответственно. Найдем F_кр для уровня значимости 0,05 и степеней свободы и при помощи функции FРАСПОБР (см. приложение 2). Для рассматриваемого примера . Т.к. в нашем случае , то остатки регрессии являются гомоскедастичными.

Рис. 1.5. Проведение теста на гетероскедастичность

остатков уравнения регрессии

 

Шаг 3. Рассчитать прогноз с помощью построенного уравнения.

Сделаем общий вывод о возможности использования построенной регрессионной модели для прогнозирования. Выполним точечный прогноз результативного показателя по полученному уравнению регрессии.

Уравнение регрессии, построенное на основе данных примера 1, имеет хорошее качество, является адекватным, его можно использовать для прогнозирования. Согласно условию планируется увеличить объем инвестиций до 19,5 тыс. д.е. Тогда объем производства должен составить: тыс. ед.

Расчет интервального прогноза с помощью построенного уравнения.

Рассчитаем ошибку прогноза по формуле

где s =В22 (рис. 1.3) – стандартная ошибка (прил. 1); n=12 – количество наблюдений; =СРЗНАЧ(С3:С14) – среднее значение фактора х; =ДИСПР(С3:С14) – дисперсия фактора х (рис. 1.1).

в этом случае предельная ошибка прогноза , а доверительный интервал .

Таким образом, прогнозное значение объема производства с вероятностью 95% должно находиться в пределах между 45,1 и 65,5 тыс. ед.

Шаг 4. Оформить отчет о проделанной работе.

План отчета.

1. Укажите фамилию, имя, название группы, номер варианта.

2. Запишите линейное уравнение регрессии в формате:

3. Дайте экономическую интерпретацию параметров уравнения.

4. Оцените тесноту линейной зависимости факторов.

5. Охарактеризуйте качество модели.

6. Сделайте вывод о статистической значимости параметров и уравнения в целом.

7. Являются ли остатки регрессии гомоскедастичными?

8. Сделайте общий вывод о качестве уравнения и возможности его использования для прогноза.

9. Рассчитайте прогнозное значение результативного фактора по известному значению независимого фактора.

Приложение 1

Протокол регрессионного анализа.

Регрессионная статистика

Наименование показателя	Принятые наименования	Формула
Множественный R	Коэффициент множественной корреляции
R-квадрат	Коэффициент детерминации R2
Нормированный R-квадрат	Скорректированный R2
Стандартная ошибка	Среднеквадратическое отклонение от модели
Наблюдения	Количество наблюдений n	n

Дисперсионный анализ

	df	SS – сумма квадратов	MS – среднее значение	F-критерий Фишера	Значимость F
Регрессия
Остаток
Итого

 

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение
Y-пересечение	b 0
x1	b 1
x2	b 2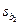
…	…	…	…	…

Приложение 2

Расчет критических значений t и F.

Значение t_кр можно получить при помощи статистической функции, которая имеет формат СТЬЮДРАСПОБР(< >; < n – m – 1>), где α – уровень значимости, по умолчанию α = 0,05; n – число наблюдений; m – количество независимых переменных в модели. Устанавливаем курсор в пустой ячейке. Вызываем команду ВСТАВКА – ФУНКЦИЯ – СТАТИСТИЧЕСКИЕ (рис. 5.1). Выбираем функцию СТЬЮДРАСПОБР и вводим значения вероятности и количества степеней свободы (рис. 5.2).

 

Рис. 5.1. Мастер функций

Рис. 5.2. Функция СТЬЮДРАСПОБР

Рис. 5.3. Функция FРАСПОБР

 

Значение F_кр можно получить при помощи статистической функции, которая имеет формат FРАСПОБР(< >; < m >; < n – m – 1>), где α – уровень значимости, по умолчанию α = 0,05; n – число наблюдений; m – количество независимых переменных в модели. Вызываем команду ВСТАВКА – ФУНКЦИЯ – СТАТИСТИЧЕСКИЕ – FРАСПОБР (рис. 5.3).

 

Поделиться:

Воспользуйтесь поиском по сайту: