 |
Проблемное и программированное обучение
|
|
|
|
Методы обучения математике
План лекции
Общая характеристика методов обучения
Методы научного познания в обучении математике
Специальые методы обучения математике
Проблемное и программированное обучение
1-вопрос.
В дидактике под методом обучения понимают «упорядоченный способ взаимосвязанной деятельности учителя и ученика, направленный на достижение целей обучения»..Процесс обучения математике представляет собой взаимодействие преподавания, учения, математического содержания
В дидактике существуют различные классификации методов обучения. Ведущими являются классификации, в основу которых положены признаки:
- Источники получения знаний (словесные, наглядные, практические методы).
- Способ усвоения изучаемого материала (объяснительно- иллюстративный,,репродуктивный, проблемное изложение, частично поисковый, исследовательский)
- Дидактические задачи (методы обучения новому материалу, формирования умений и навыков, контроля).
- Элементы любой деятельности (методы стимулирования и мотивации, организации и осуществления учебно-познавательной деятельности, контроля и самоконтроля и др.)
Систему методов обучения математике условно можно разделить на общие и специальные. Общие также можно разделить на методы научного познания, и общедидактические, адаптированные к содержанию обучения математике.
3-вопрос
В методике к специальным методам обучения математике относят метод математического моделирования и аксиоматический метод. Рассмотрим их более подробно.
Одним из наиболее плодотворных методов познания действительности является методпостроения математических моделей изучаемых объектов и процессов.
|
|
|
Математическая модель –это приближенное описание какого-либо класса явлений,
на языке определенной математической теории с помощью уравнений, неравенств и их систем, функций, системы геометрических предложений или других математических объектов.
В процессе математического моделирования выделяют три этапа:
- Формализация - перевод исходной задачи на язык математики, то есть построение математической модели.
- Внутримодельное решение - решение задачи в рамках математической теории
- Интерпретация – перевод результата решения математической задачи на язык исходной ситуации.
Иногда говорят и о четвертом этапе метода математического моделирования – исследование полученных результатов и совершенствование модели.
Пример. В детский сад привезли всего 120 столов и стульев. Известно, что что стульев на 72 больше, чем столов. Сколько стульев и столов привезли?
1. Формализация. . Составляем арифметическую модель задачи:
1)120- 72; 2) (120 -72):2; 3)) (120 -72):2 + 72.
Алгебраическая модель
Пусть Х - количество столов; У- количество стульев. Получим систему:
Х+У = 120
У –Х = 72 
Внутримодельное решение 


Решив систему, получим:Х = 24, У= 96
Интерпретация
Ответ: Привезли 24 стола, 96 стульев.
Улучшить алгебраическую модель можно, обозначив количество стульев через Х+72.
Примерами проявления метода математического моделирования при решении задач является использование
· координатного метода, когда свойства геометрических фигур выражаются на аналитическом языке в виде уравнений, неравенств, функций или других математических объектов, а затем переводятся на геометрический язык;
· векторного метода;
· метода геометрических преобразований;
· метода дифференциального исчисления, когда поведение функции можно исследовать с помощью производной
Одним из основных целей обучения математике в школе является показ возможностей использования математики для решения практических задач, достижение которого невозможно без формирования учащихся строить и исследовать математические модели.
|
|
|
Так, отталкиваясь от физических процессов (например, свободное падение, центробежная сила, электрическое напряжение), появляется математическая модель ситуации – квадратичная функция У= ах2 + вх +с. Исследование модели сводится к исследованию квадратичной функции. После этого появляется возможность использования новых теоретических знаний (свойства квадратичной функции) для изучения реальных явлений и процессов.
Аксиоматический метод – способ построения научной теории, когда в ее основу кладутся некоторые исходные положения (аксиомы, постулаты), из которых все остальные утверждения этой науки (теоремы) должны выводиться чисто логическим путем посредством доказательств (БСЭ -3е изд.,1969,т.1,с.345). Иногда аксиоматический метод называют дедуктивным методом, подчеркивая тем самым, что доказательства проводятся с использованием правил логического вывода.
Общая схема и пример обучения аксиоматизации.
Общая схема Пусть при описании реальной ситуации получено множество М, состоящее из: предложений р1, р2, р3, …рк.,где к>1 Возникает проблема: каковы логические связи между предложениями из М, то есть из какого подмножества А множества М предложений можно вывести все остальные с использованием уже
имеющихся знаний Г. Исследование этой проблемы имеет в качестве результата построение маленькой теории, то есть нахождение такой системы А, для которой имеет место Г.А  Рi, 1
Рi, 1 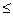 I
I 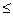 k
k 
Пример. На рисунке 
изображена ситуация, которую можно описать следующим образом: -
1) Р1: О  [AB]; 2) P2:
[AB]; 2) P2: 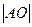 =
=  ; 3) P3: Z0(A)=B; 4)/ P4: Z9([A]})= [BA]
; 3) P3: Z0(A)=B; 4)/ P4: Z9([A]})= [BA]
Встает вопрос: нужно ли приводить все 3 описания,, чтобы знать о ситуации?
Очевидно, что Р2 не следует из Р1:, так как из того, что точка О принадлежит отрезку АВ не следует, что эта точка является его серединой. Р1 также не следует из P2 в силу того, точка О может не принадлежать отрезку АВ...Здесь возможны 4 ситуации: а)из Р1 и P2 следует P3:, а из P3: - P4; б)из P3 следуют и Р1, и P2; в)из P4 следуют и Р1, и P2.,и P3.
Аксиоматический метод, как метод построения теорий, может быть адаптирован и как метод обучения математике. Здесь речь может идти о построении «маленькой» теории в рамках небольшой темы.
|
|
|
Обучение аксиоматизации имеет два аспекта:
· умение выделять из множества предложений исходные и доказывать на их базе остальныхе;
· отвлечение от конкретной природы объектов и переход на более высокую степень абстрагирования (на факультативных занятиях, в старших классах) на хорошо подобранных примерах.
Проблемное обучение - это обучение, протекающее в виде разрешения последовательно создаваемых проблемных ситуаций. Организация проблемного обучения предполагает качественно новое взаимодействие учителя и учащихся, организацию учителем самостоятельного овладения учащимися знаний, специфическое построение учебного материала: с выделение ведущих идей курса, их развития, содержательное обобщение. При этом познание учащихся происходит как исследование в процессе интеллектуальной учебной деятельности
Пример. В 8-м классе после ознакомления с понятием «параллелограмм», его свойствами и признаками, учащиеся выполняют перегибание различных моделей параллелограмма, приходят к выводу, что некоторые из них имеют ось симметрии.. Далее исследуются свойства параллелограмма, имеющего ось симметрии., учащиеся замечают, что частные случаи параллелограмма (прямоугольник, ромб, квадрат) отличаются друг от друга расположением и числом осей симметрии. Затем изучаются эти виды параллелограмма, выделяются их общие свойства, различия, рассматриваются практические приложения полученных результатов.
Проблемное обучение на уровне средней школы обеспечивается эвристическим исследовательскими методами, на уровне высшей школы- методом проблемного изложения знаний исследовательским методом.
Проблемное изложение – метод, при котором учитель излагает путь исследования, поиска и открытия новых знаний.
Эвристический метод сочетает изложение учителем учебного материала и творческий поиск учащихся.
Исследовательский метод позволяет строить процесс обучения подобно процессу научного исследования: выявляются неясные и неизвестные факты, подлежащие исследованию; уточняется и формулируется проблема; выдвигается гипотеза; составляется план исследования; осуществляется план с последующей проверкой выдвинутой гипотезы..
|
|
|
Проблемная ситуация - это осознанное затруднение, возникшее в результате несоответствия между имеющимися знаниями учащихся и теми, которые необходимы для решения поставленной задачи 
Задача, создающая проблемную ситуацию, называется проблемной задачей Требования к проблеме:
· доступность для пониманию учащихся;
· вызывает интерес;
· естественность постановки;
· проблемную ситуацию следует готовить, она должна создаваться всем ходом урока и быть его органической частью.
Пути создания проблемной ситуации:
· предварительная постановка практической.проблемы;
· разбор возможностей использования изученного материала;
· поиск средств выполнения задания;
· решение нешаблонных задач (например, логические задачи, задачи на исследование).
Приемы создания проблемной ситуации: постановка эксперимента; поиск метода решения задачи; использование средств наглядности; проведение лабораторных и практических работ; использование занимательных сюжетов; составление задач по теме.
Проблемное обучение позволяет эффективно сочетать индивидуальную и групповую работу учащихся. При этом необходимо предусмотреть строгий контроль и учет поисковой деятельности учащихся, их творческую активность в течение всего урока; особое внимание уделить постановке домашнего задания.
Постановка уроков проблемного типа требуют больших затрат учебного времени, и поэтому не могут осуществляться каждый день. Также существуют темы, изучать которые целесообразно традиционными методами В то же время бессистемное, эпизодическое построение проблемных уроков не дают эффекта.
Программированное обучение осуществляется с помощью обучающей программы, материал подается в форме строгой последовательности «кадров»
Каждый кадр содержит порцию нового материала, контрольный вопрос или задание. Программированное обучение предусматривает:
1. Правильный отбор учебного материала;
2. Рациональную дозировку его подачи;
3. Активную самостоятельную деятельность учащегося по усвоению материала;
4. Обеспечение возможности каждому ученику работать со свойственным ему скоростью усвоения;
5. Постоянный контроль за деятельностью обучаемого.
Существуют две системы программированного учебного материала – линейная и разветвленная программы. В линейной программе учебный материал подается небольшими порциями (кадрами), включающими простой вопрос по изучаемому материалу. Прочтя вопрос, ученик должен на него правильно ответить, а затем перейти к следующему кадру.
|
|
|
При разветвленном программировании учебный материал дается в виде кадров, несущих более обширную информацию, чем при линейном. Вопрос по проверке усвоения не предполагает однозначного ответа: в конце кадра помещена серия ответов, среди которых только один правильный. Ошибочные ответы даются с учетом наиболее вероятных ошибок учащихся. Против каждого ответа указывается страница, к которой должен обратиться ученик.
Достоинством линейного программировании является то, что ученик самостоятельно формулирует свои ответы, и только потом проверяет себя.. При разветвленном программировании учитываются индивидуальные особенности ученика (он продвигается со свойственной ему скоростью), но при этом он пользуется готовыми ответами
Приведем примеры линейной и разветвленной программ.
Линейная программа.
Известно, что при вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель оставляют тот же.. Например,  -
-  =
= 
 1. Вычисли:
1. Вычисли: 

 (
( )
)
2. Известно, что  -
-  =
=  (7)
(7)
3. Реши уравнение: 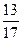 - х -
- х - 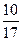 (
( )
)
4. Вычисли значение выражения: в-  , если в =
, если в = 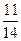 (
( )
)
5. Вычисли: ( -
-  ) -
) - 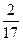 (
( ).
).
Разветвленная программа.
Стр.1.
Результат умножения чисел называется произведением этих чисел. Важным является случай, когда сомножителями являются равные числа. Так, в примере 3 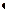 3 = 9 число 3 появляется в качестве сомножителя два раза. Использовать одно и тоже число в качестве сомножителей можно более чем два раза.
3 = 9 число 3 появляется в качестве сомножителя два раза. Использовать одно и тоже число в качестве сомножителей можно более чем два раза.
Чему равно произведение, если число 2 используется сомножителем три раза.?
Ответ См. стр.
6 2
8 4
9 3
Предположим, что ученик выбрал ответ: число 6.
Стр. 2.
«Ваш ответ: «Если 2 берется сомножителем 3.раза, то произведение равно 6». Вы просто использовали 2 и 3 как сомножители: 2  3=6. Это неверно..
3=6. Это неверно..
Мы хотим узнать, какой результат вы получите, если возьмете число 2 сомножителем 3 раза. Другими словами, мы хотим узнать результат умножения 2  2
2  2 =?. Теперь вернитесь к предыдущей странице и выберите правильный ответ».
2 =?. Теперь вернитесь к предыдущей странице и выберите правильный ответ».
Предположим, что ученик выбрал правильный ответ. В этом случае он должен открыть стр. 4.
Стр.4.
«Ваш ответ: 8. Он верен. Тот факт, что число 2 берется сомножителем 3 раза, записывается следующим образом: 23, где 2 –основание степени, 3- показатель степени. Что означает запись 34?
Ответ См. стр.
12 7
64 15
81 6»..
Идеи программированного обучения.не нашли в школе широкого применения. Это связано с тем,
· Программированный учебник по сравнению с обычным учебником в меньшей степени готовит к самостоятельному приобретению знаний;
· Выпускнику школы придется работать преимущественно с непрограммированными пособиями;
· Издание программированных учебников требует больших материальных затрат;
· Применение программированных учебников значительно снижает роль учителя, ведет к недооценке его живого слова.
Но в последнее время в связи с компъютеризацией учебного процесса возможно оживление идеи программированного обучения,
|
|
|


