 |
Глава II. Свойства метризуемых пространств
|
|
|
|
Метризуемость топологических пространств
Выполнила
студентка 5 курса
математического факультета
Побединская Татьяна Викторовна
_______________________________
(подпись)
Научный руководитель
к.ф.-м.н., доцент кафедры математического анализа и МПМ Варанкина Вера Ивановна
_______________________________
(подпись)
Рецензент
_______________________________
(подпись)
Допущена к защите в ГАК
Зав. кафедрой______________________________к.п.н., доцент Крутихина М.В.
(подпись)
«_____» _______________2004 г.
Декан факультета_________________________к.ф.-м.н., доцент Варанкина В.И.
(подпись)
«_____» _______________2004 г.
КИРОВ
2004
Содержание
Введение. 3
Глава I. Основные понятия и теоремы.. 4
Глава II. Свойства метризуемых пространств. 10
Глава III. Примеры метризуемых и неметризуемых пространств. 21
Библиографический список. 24
Введение
Тема дипломной работы – «Метризуемость топологических пространств».
В первой главе работы вводятся основные определения, связанные с понятиями метрического и топологического пространств.
Во второй главе рассматриваются и доказываются следующие свойства метризуемых пространств:
1. Метризуемое пространство хаусдорфово.
2. Метризуемое пространство нормально.
3. В метризуемом пространстве  выполняется первая аксиома счетности.
выполняется первая аксиома счетности.
|
|
|
4. Метризуемое пространство совершенно нормально.
5. Для метризуемого пространства  следующие условия эквивалентны:
следующие условия эквивалентны:
1)  сепарабельно,
сепарабельно,
2)  имеет счетную базу,
имеет счетную базу,
3)  финально компактно.
финально компактно.
6. Любое метризуемое топологическое пространство может быть метризовано ограниченной метрикой.
7. Произведение счетного числа метризуемых пространств метризуемо.
В третьей главе рассматриваются примеры метризуемых и неметризуемых пространств.
Глава I. Основные понятия и теоремы
Определение. Метрическим пространством называется пара 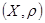 , состоящая из некоторого множества (пространства)
, состоящая из некоторого множества (пространства)  элементов (точек) и расстояния, то есть однозначной неотрицательной действительной функции
элементов (точек) и расстояния, то есть однозначной неотрицательной действительной функции  , определенной для любых
, определенной для любых 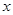 и
и  из
из  и удовлетворяющей трем условиям:
и удовлетворяющей трем условиям:
1) 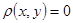
 (аксиома тождества);
(аксиома тождества);
2)  (аксиома симметрии);
(аксиома симметрии);
3)  (аксиома треугольника).
(аксиома треугольника).
Определение. Пусть  – некоторое множество. Топологией в
– некоторое множество. Топологией в  называется любая система
называется любая система  его подмножеств
его подмножеств  , удовлетворяющая двум требованиям:
, удовлетворяющая двум требованиям:
1. Само множество  и пустое множество принадлежат
и пустое множество принадлежат  .
.
2. Объединение  любого (конечного или бесконечного) и пересечение
любого (конечного или бесконечного) и пересечение  любого конечного числа множеств из
любого конечного числа множеств из  принадлежат
принадлежат  .
.
Множество  с заданной в нем топологией
с заданной в нем топологией  , то есть пара
, то есть пара 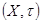 , называется топологическим пространством.
, называется топологическим пространством.
Множества, принадлежащие системе  , называются открытыми.
, называются открытыми.
Множества  , дополнительные к открытым, называются замкнутыми множествами топологического пространства
, дополнительные к открытым, называются замкнутыми множествами топологического пространства  .
.
Определение. Совокупность  открытых множеств топологического пространства называется базой топологического пространства
открытых множеств топологического пространства называется базой топологического пространства  , если всякое открытое множество в
, если всякое открытое множество в  может быть представлено как объединение некоторого числа множеств из
может быть представлено как объединение некоторого числа множеств из 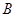 .
.
Теорема 1. Всякая база 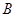 в топологическом пространстве
в топологическом пространстве  обладает следующими двумя свойствами:
обладает следующими двумя свойствами:
1) любая точка  содержится хотя бы в одном
содержится хотя бы в одном 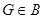 ;
;
2) если 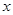 содержится в пересечении двух множеств
содержится в пересечении двух множеств 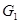 и
и 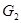 из
из 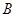 , то существует такое
, то существует такое 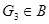 , что
, что  .
.
|
|
|
Определение. Открытым шаром или окрестностью точки 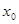 радиуса
радиуса 
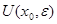 в метрическом пространстве
в метрическом пространстве  называется совокупность точек
называется совокупность точек  , удовлетворяющих условию
, удовлетворяющих условию 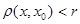 . При этом
. При этом  – центр шара,
– центр шара,  – радиус шара.
– радиус шара.
Утверждение 1. Для любого 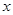 , принадлежащего
, принадлежащего  -окрестности точки
-окрестности точки 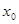 , существует окрестность радиуса
, существует окрестность радиуса 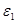 , включенная в
, включенная в  -окрестность точки
-окрестность точки 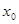 .
.
Доказательство. Выберем в качестве 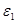 :
: 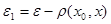 .
.
Достаточно доказать для произвольного  импликацию
импликацию  . Действительно, если
. Действительно, если  , то
, то 
Получаем, что  , что и требовалось доказать.
, что и требовалось доказать.
Теорема 2. Совокупность всех открытых шаров образуют базу некоторой топологии.
Доказательство. Проверим свойства базы (теорема 1).
· Свойство первое очевидно, так как для любого  выполняется
выполняется  для любого
для любого  .
.
· Проверим второе свойство.
Пусть  ,
,  и
и 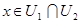 , тогда, воспользовавшись утверждением 1, найдем такое
, тогда, воспользовавшись утверждением 1, найдем такое 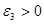 , что
, что  Теорема доказана.
Теорема доказана.
Определение. Топологическое пространство 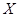 метризуемо, если существует такая метрика
метризуемо, если существует такая метрика  на множестве
на множестве 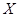 , что порожденная этой метрикой топология совпадает с исходной топологией пространства
, что порожденная этой метрикой топология совпадает с исходной топологией пространства 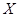 .
.
Аксиомы отделимости
Аксиома  . Для любых двух различных точек топологического пространства окрестность хотя бы одной из них не содержит другую.
. Для любых двух различных точек топологического пространства окрестность хотя бы одной из них не содержит другую.
Аксиома  . Каждая из двух произвольных точек пространства имеет окрестность, не содержащую вторую точку.
. Каждая из двух произвольных точек пространства имеет окрестность, не содержащую вторую точку.
Предложение. 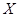 является
является  - пространством тогда и только тогда, когда для любого
- пространством тогда и только тогда, когда для любого  множество
множество  замкнуто.
замкнуто.
Доказательство.
Необходимость. Пусть  . Так как
. Так как 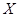 является
является  -пространством, то существует окрестность
-пространством, то существует окрестность  , не содержащая
, не содержащая 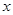 .
.
Рассмотрим 
Докажем, что  . Применим метод двойного включения:
. Применим метод двойного включения:
· Очевидно, что 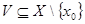 по построению множества
по построению множества  .
.
· 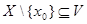 .
.
Пусть 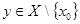 отсюда для любого
отсюда для любого  отличного от
отличного от  существует окрестность
существует окрестность 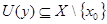 , значит
, значит 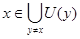 , тогда
, тогда 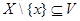 .
.
Множество  - открыто, как объединение открытых множеств.
- открыто, как объединение открытых множеств.
Тогда множество  - замкнуто, как дополнение открытого множества.
- замкнуто, как дополнение открытого множества.
Достаточность. Рассмотрим  . По условию
. По условию 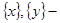 замкнутые множества. Так как
замкнутые множества. Так как  , то
, то  . Множество
. Множество 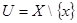 -открыто как дополнение замкнутого и не содержит
-открыто как дополнение замкнутого и не содержит  . Аналогично доказывается существование окрестности точки
. Аналогично доказывается существование окрестности точки  , не содержащей точку
, не содержащей точку 
Что и требовалось доказать.
Аксиома 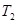 (аксиома Хаусдорфа). Любые две точки пространства имеют непересекающиеся окрестности.
(аксиома Хаусдорфа). Любые две точки пространства имеют непересекающиеся окрестности.
|
|
|
Аксиома  . Любая точка и не содержащее ее замкнутое множество имеют непересекающиеся окрестности.
. Любая точка и не содержащее ее замкнутое множество имеют непересекающиеся окрестности.
Определение. Пространства, удовлетворяющие аксиомам  (
(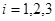 ) называются
) называются  -пространствами (
-пространствами (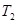 -пространства называют также хаусдорфовыми пространствами).
-пространства называют также хаусдорфовыми пространствами).
Определение. Пространство называется нормальным или  -пространством, если оно удовлетворяет аксиоме
-пространством, если оно удовлетворяет аксиоме  , и всякие его два непустые непересекающиеся замкнутые множества имеют непересекающиеся окрестности.
, и всякие его два непустые непересекающиеся замкнутые множества имеют непересекающиеся окрестности.
Определение. Система окрестностей называется определяющей системой окрестностей точки 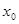 , если для любой окрестности
, если для любой окрестности  точки
точки  найдется окрестность из этой системы, содержащаяся в
найдется окрестность из этой системы, содержащаяся в 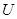 .
.
Определение. Если точка 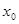 топологического пространства имеет счетную определяющую систему окрестностей, то говорят, что в этой точке выполняется первая аксиома счетности. Если это верно для каждой точки пространства, то пространство называется пространством с первой аксиомой счетности.
топологического пространства имеет счетную определяющую систему окрестностей, то говорят, что в этой точке выполняется первая аксиома счетности. Если это верно для каждой точки пространства, то пространство называется пространством с первой аксиомой счетности.
Определение. Две метрики  и
и 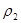 на множестве
на множестве 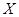 называются эквивалентными, если они порождают на нем одну и ту же топологию.
называются эквивалентными, если они порождают на нем одну и ту же топологию.
Пример. На плоскости  для точек
для точек  и
и 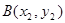 определим расстояние тремя различными способами:
определим расстояние тремя различными способами:
1.  ,
,
2.  ,
,
3.  .
.
· Введенные расстояния являются метриками. Проверим выполнимость аксиом метрики для введенных расстояний.
1. 1) 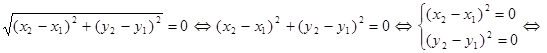
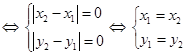
2) так как  и
и  , то вторая аксиома очевидна:
, то вторая аксиома очевидна: 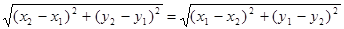
3) рассмотрим точки  ,
, 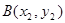 ,
, 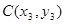 и докажем следующее неравенство:
и докажем следующее неравенство:

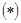
Возведем это неравенство в квадрат:



 .
.
Так как 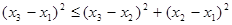 и
и  (поскольку
(поскольку 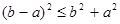 ) и выражение
) и выражение 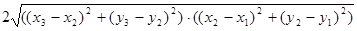 есть величина неотрицательная, то неравенство
есть величина неотрицательная, то неравенство 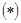 является верным.
является верным.
2. 1) 
2) так как  и
и 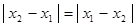 , то вторая аксиома очевидна:
, то вторая аксиома очевидна: 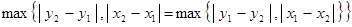 .
.
3) рассмотрим точки  ,
, 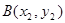 ,
, 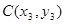 и докажем следующее неравенство:
и докажем следующее неравенство:  .
.
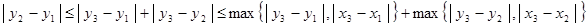

Тогда и 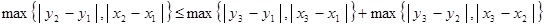 .
.
3. 1) 
2) так как 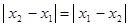 и
и  , то вторая аксиома очевидна:
, то вторая аксиома очевидна:
 .
.
3) рассмотрим точки  ,
, 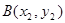 ,
, 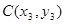 .
.
Неравенство: 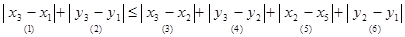 - очевидно.
- очевидно.
· Введенные метрики 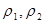 и
и  эквивалентны, то есть задают одну и ту же топологию.
эквивалентны, то есть задают одну и ту же топологию.
Пусть метрика  порождает топологию
порождает топологию 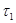 ,
, 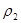 - топологию
- топологию  и
и  - топологию
- топологию 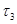 . Достаточно показать два равенства.
. Достаточно показать два равенства.
|
|
|
Покажем, что 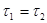 .
.
Рассмотрим множество, 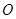 открытое в
открытое в  и покажем, что
и покажем, что  открыто в
открыто в  . Возьмем некоторую точку и изобразим шар с центром в этой точке, который целиком лежит в
. Возьмем некоторую точку и изобразим шар с центром в этой точке, который целиком лежит в 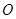 . Шар в
. Шар в  - квадрат, шар в
- квадрат, шар в  - круг. А квадрат всегда можно заключить в круг. Тогда
- круг. А квадрат всегда можно заключить в круг. Тогда 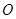 открыто и в
открыто и в  .
.
Аналогично доказывается, что  . А тогда и
. А тогда и  .
.
Глава II. Свойства метризуемых пространств
Свойство 1. Метризуемое пространство хаусдорфово.
Доказательство. Пусть 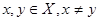 . Возьмем
. Возьмем  . Докажем, что
. Докажем, что  .
.
Предположим, что  , тогда существует
, тогда существует 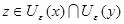 , т.е.
, т.е. 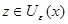 и
и  . Тогда,
. Тогда, 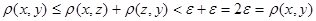 . Получили противоречие. Следовательно,
. Получили противоречие. Следовательно,  .
.
Следствие. Метризуемое пространство является 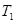 - пространством.
- пространством.
Определение. Расстоянием от точки  до множества
до множества 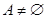 в метрическом пространстве называется
в метрическом пространстве называется 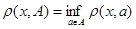 .
.
Утверждение 2. Пусть множество 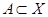 фиксировано; тогда функция
фиксировано; тогда функция  , сопоставляющая каждой точке
, сопоставляющая каждой точке  расстояние
расстояние  , непрерывна на пространстве
, непрерывна на пространстве  .
.
Доказательство. Воспользуемся определением непрерывности: функция 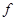 называется непрерывной в точке
называется непрерывной в точке  , если
, если  .
.
Из неравенства  , где
, где  , получаем
, получаем  . Аналогично
. Аналогично 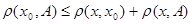 . Из полученных неравенств следует
. Из полученных неравенств следует 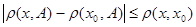 .
.
Для произвольного  возьмем
возьмем  . Тогда из неравенства
. Тогда из неравенства  следует
следует  . Непрерывность
. Непрерывность 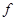 доказана.
доказана.
Лемма.  – замкнутое множество в метрическом пространстве
– замкнутое множество в метрическом пространстве 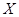 . Для любого
. Для любого  расстояние от
расстояние от  до множества
до множества  положительно.
положительно.
Доказательство.
Множество  замкнуто, отсюда следует, что множество
замкнуто, отсюда следует, что множество  - открыто. Так как точка
- открыто. Так как точка 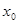 принадлежит открытому множеству
принадлежит открытому множеству  , то существует такое
, то существует такое 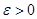 , что
, что  . Так как
. Так как  , то
, то  для некоторого
для некоторого 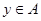 . Поэтому
. Поэтому 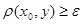 для любого
для любого 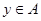 . Следовательно,
. Следовательно, 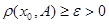 , что и требовалось доказать.
, что и требовалось доказать.
Свойство 2. Метризуемое пространство нормально.
Доказательство. По доказанному метризуемое пространство является
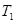 -пространством. Остается доказать, что любые непустые непересекающиеся замкнутые множества
-пространством. Остается доказать, что любые непустые непересекающиеся замкнутые множества  и
и 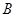 имеют непересекающиеся окрестности.
имеют непересекающиеся окрестности.
Так как 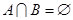 и множество
и множество 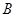 замкнуто по условию, то для любого
замкнуто по условию, то для любого 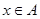 по лемме
по лемме  .
.
Обозначим 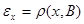 и
и 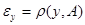 для произвольных
для произвольных 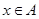 и
и 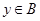 .
.
Множества  и
и  открыты как объединения открытых шаров в
открыты как объединения открытых шаров в  и содержат соответственно множества
и содержат соответственно множества  и
и 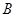 .
.
Следовательно,  - окрестность множества
- окрестность множества  ,
, 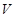 - окрестность множества
- окрестность множества  .
.
Докажем, что  .
.
Предположим, что 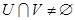 , то есть
, то есть  . Тогда из условия
. Тогда из условия 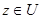 следует, что
следует, что 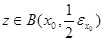 для некоторого
для некоторого  . Отсюда
. Отсюда  .
.
Аналогично получаем  для некоторого
для некоторого 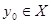 . Для определенности пусть
. Для определенности пусть  . Тогда
. Тогда 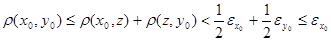 .
.
Получаем  , для некоторой точки
, для некоторой точки  , что невозможно в силу определения расстояния от точки до множества.
, что невозможно в силу определения расстояния от точки до множества.
Следовательно  . Таким образом,
. Таким образом,  является
является  -пространством, а, значит, нормальным пространством. Теорема доказана.
-пространством, а, значит, нормальным пространством. Теорема доказана.
Свойство 3. В метризуемом пространстве  выполняется первая аксиома счетности.
выполняется первая аксиома счетности.
|
|
|
Доказательство. Пусть 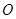 - произвольное открытое множество, содержащее точку
- произвольное открытое множество, содержащее точку  . Так как открытые шары образуют базу топологии метрического пространства, то
. Так как открытые шары образуют базу топологии метрического пространства, то  содержится в
содержится в 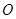 вместе с некоторым открытым шаром, то есть
вместе с некоторым открытым шаром, то есть 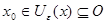 для некоторых
для некоторых  и
и 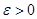 . По утверждению 1 найдется такое
. По утверждению 1 найдется такое  , что
, что 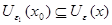 .
.
Возьмем  , для которого
, для которого 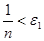 . Тогда
. Тогда 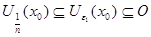 . Таким образом открытые шары
. Таким образом открытые шары  ,
,  образуют определяющую систему окрестностей точки
образуют определяющую систему окрестностей точки  . Очевидно, что множество этих окрестностей счетно. Что и требовалось доказать.
. Очевидно, что множество этих окрестностей счетно. Что и требовалось доказать.
Определение. Множеством типа  или просто
или просто  - множеством пространства
- множеством пространства 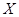 называется всякое множество
называется всякое множество  , являющееся объединением счетного числа замкнутых (в
, являющееся объединением счетного числа замкнутых (в  ) множеств.
) множеств.
Определение. Множеством типа 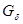 или просто
или просто 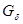 - множеством пространства
- множеством пространства 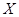 называется всякое множество
называется всякое множество  , являющееся пересечением счетного числа открытых (в
, являющееся пересечением счетного числа открытых (в  ) множеств.
) множеств.
Очевидно, что множества типа  и
и 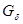 являются взаимно дополнительными друг для друга.
являются взаимно дополнительными друг для друга.
Определение. Нормальное пространство, в котором всякое замкнутое множество является множеством типа 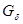 , называется совершенно нормальным.
, называется совершенно нормальным.
Утверждение 3. Нормальное пространство является совершенно нормальным тогда и только тогда, когда всякое открытое множество, принадлежащее этому пространству, является множеством типа  .
.
Свойство 4. Метризуемое пространство совершенно нормально.
Доказательство. Пусть  - непустое замкнутое множество в
- непустое замкнутое множество в 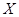 . Тогда
. Тогда  для непрерывной функции
для непрерывной функции 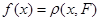 (непрерывность ее установлена в утверждении 2). Обозначим
(непрерывность ее установлена в утверждении 2). Обозначим  , множества
, множества  открыты в
открыты в 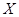 как прообразы открытых множеств при непрерывном отображении. Докажем, что
как прообразы открытых множеств при непрерывном отображении. Докажем, что 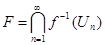 .
.
Пусть 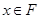 , тогда
, тогда  . Так как
. Так как 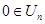 для любого
для любого  , то
, то  для любого
для любого  . Отсюда
. Отсюда  .
.
Обратно. Пусть  , тогда
, тогда  для любого
для любого 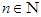 . Отсюда
. Отсюда 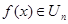 для любого
для любого  , поэтому
, поэтому  для любого
для любого  , тогда
, тогда 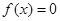 , значит
, значит 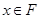 . Таким образом множество
. Таким образом множество  является множеством типа
является множеством типа  .
.
Определение. Множество 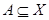 всюду плотно в
всюду плотно в  , если любое непустое открытое в
, если любое непустое открытое в  множество содержит точки из
множество содержит точки из  .
.
Определение. Топологическое пространство  называется сепарабельным, если оно имеет счетное всюду плотное подмножество.
называется сепарабельным, если оно имеет счетное всюду плотное подмножество.
Определение. Семейство γ открытых в  множеств образуют покрытие пространства
множеств образуют покрытие пространства  , если
, если  содержится в объединении множеств этого семейства.
содержится в объединении множеств этого семейства.
Определение. Топологическое пространство  называется финально компактным, если из любого его открытого покрытия можно выделить счетное подпокрытие.
называется финально компактным, если из любого его открытого покрытия можно выделить счетное подпокрытие.
Свойство 5. Для метризуемого пространства  следующие условия эквивалентны:
следующие условия эквивалентны:
1)  сепарабельно,
сепарабельно,
2)  имеет счетную базу,
имеет счетную базу,
3)  финально компактно.
финально компактно.
Доказательство. 
Пусть 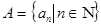 - счетное всюду плотное множество в
- счетное всюду плотное множество в 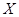 ,
,  - метрика в
- метрика в 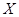 . Множество окрестностей
. Множество окрестностей 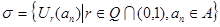 счетно. Докажем, что
счетно. Докажем, что 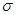 - база топологии в
- база топологии в  . Пусть
. Пусть  - произвольное открытое в
- произвольное открытое в  множество,
множество,  . Тогда
. Тогда  для некоторого
для некоторого  . Рассмотрим рациональное число
. Рассмотрим рациональное число  , для которого
, для которого 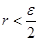 и точку
и точку  , для которой
, для которой  .
.
Докажем, что 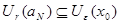 . Пусть
. Пусть  . Так как
. Так как  , то
, то  . Тогда
. Тогда  . Таким образом, для произвольного
. Таким образом, для произвольного 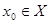 и открытого множества
и открытого множества  нашелся элемент из
нашелся элемент из  , такой, что
, такой, что  . Следовательно
. Следовательно 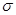 - база топологии.
- база топологии.
 Пусть
Пусть  - счетная база в
- счетная база в  . Рассмотрим произвольное открытое покрытие множества
. Рассмотрим произвольное открытое покрытие множества  ,
, 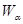 - открыты для любого
- открыты для любого  (
( - индексное множество). Для любого
- индексное множество). Для любого  существует
существует 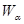 , для которого
, для которого  . Так как
. Так как 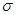 - база, то найдется такое
- база, то найдется такое 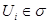 , что
, что  . Тогда
. Тогда  . Поскольку база
. Поскольку база 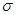 счетна, то
счетна, то  покрывается счетным числом соответствующих множеств
покрывается счетным числом соответствующих множеств  . Таким образом,
. Таким образом,  - финально компактно.
- финально компактно.
 Для каждой точки
Для каждой точки  рассмотрим окрестности
рассмотрим окрестности  , которые образуют покрытие пространства
, которые образуют покрытие пространства  . В силу финальной компактности
. В силу финальной компактности 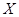 из этого покрытия можно выделить счетное подпокрытие
из этого покрытия можно выделить счетное подпокрытие 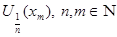 . В каждом из этих множеств выберем точку
. В каждом из этих множеств выберем точку 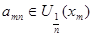 . Множество точек
. Множество точек 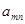 счетно, докажем, что оно плотно в
счетно, докажем, что оно плотно в 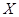 . Пусть
. Пусть  - произвольное открытое множество в
- произвольное открытое множество в  ,
, 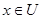 , тогда
, тогда  для некоторого
для некоторого 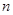 . Существует элемент подпокрытия
. Существует элемент подпокрытия 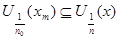 . Тогда
. Тогда  , то есть любое непустое открытое множество в
, то есть любое непустое открытое множество в  содержит точ
содержит точ
|
|
|


