 |
Полуавтоматическая подгонка/сглаживание
|
|
|
|
FastShip имеет функцию fit-surface для автоматической подгонки контрольной сетки под ординаты. Проектировщик сперва создаёт поверхность, близкую по форме к ординатам, с необходимыми топологическими особенностями (сломы и т.д.). Эта функция корректно работает в той области поверхности, которая не содержит сломов и может давать непредсказуемые результаты у края поверхности, так что проектировщик вынужден вручную управлять краями поверхности и её сломами. Эти области можно исключить из работы функции fit-surface путём выполнения функции freeze-net, перед тем, как продолжать выполнение функции fit-surface. Функция fit-surface ни добавляет, ни удаляет ряды или столбцы поверхности; она только двигает существующие вершины. Она сохраняет плотность поверхности, т.е. не создаёт слишком загромождённой поверхности. Функция fit-surface может выборочно применяться к одному участку поверхности, не затрагивая остальной поверхности.
Команду fit-surface особенно эффективно применять при итерационных процессах, чередуя сглаживания проектировщика с подгонкой машины. Поэтому гладкость всё-таки остаётся делом проектировщика с обычными инструментами для её измерения. Если результат работы команды fit-surface точно удовлетворяет ординатам, но по мнению проектировщика поверхность не гладка, операцию можно отменить командой undo. Лучший метод заключается в следующем: вручную создаётся поверхность с нужной гладкостью, а затем снова запускается команда fit-surface (команда fit-surface может занять от 3 до 20 секунд, в зависимости от вашего компьютера, плотности ординат и сложности поверхности). Этот процесс может продолжаться настолько долго, пока не будет найдено оптимального соотношения между гладкостью поверхности и её схожести ординатам.
|
|
|
Итоги
Создание поверхности по ординатам – сложная задача, имеющая множество различных аспектов. Она состоит из нескольких промежуточных задач, каждая из которых имеет свои сложности. Очень редко решение этих задач автоматически даёт удовлетворительные результаты.
Решение задачи с помощью сплайнов имеет тенденцию загромождать модели, которые могут содержать осцилляции, трудно удаляемые даже вручную. К тому же они могут сглаживать или терять отличительные особенности поверхности. По этой причине сплайны не находят применения при решении задач подобного рода. NURBS поверхности также страдают при автоматическом методе и теряют топологические особенности поверхности. Лучшим решением данной задачи является применение полуавтоматического метода с использованием NURBS поверхностей, когда проектировщик сам создаёт поверхность с нужной ему топологией, которую затем обрабатывает компьтер для получения более точного соответствия поверхности ординатам. Важно, чтобы проектировщик понимал качество снятых ординат и знал, нужно и возмоно ли точно подогнать поверхность по ординатам. Если поверхность нужна лишь для промежуточных расчётов или для расчёта гидростатики, то гладкости можно не уделять большого внимания, а точность не слишком важна, пока не будут точно установлены водоизмещение, центр величины и т.д. В любом случае гладкость стоит на первом месте перед точностью, т.е. ординаты могут быть и не подогнаны точно. В этом случае ручной и полуавтоматические методы более продуктивны и обеспечивают лёгкость и надёжность метода.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ NURBS
Что такое NURBS
Сперва определимся, что же действительно значит термин NURBS. NURBS-нестандартный рациональный В-сплайн. Попытаемся расшифровать каждую часть этого многогранного понятия. Корневым словом NURBS является слово В-сплайн. Что это такое В-сплайн? Здесь важно понять‚ что говоря NURBS имеется в виду поверхность NURBS или кривая NURBS. Для простоты суждения первоначально рассмотрим кривые NURBS‚ а потом осуществим переход к поверхностям NURBS. Говоря вкратце‚ В-сплайн-это кривая‚ созданная с использованием вершин определяющего многоугольника‚ интерполирующая определённым образом для установления взаимосвязи между кривой и определяющего многоугольника. Этому свойству удовлетворяет не одна кривая‚ созданная определяющим многоугольником. Отличительной чертой В-сплайна является взаимосвязь между кривой и определяющим многоугольником‚ представленная в виде последовательности функций многочленов‚ называемых базисными функциями В-сплайна. Прежде чем понять‚ что это значит‚ немного отвлекёмся для описания ключевых терминов NURBS.
|
|
|
Терминология NURBS
Сперва поговорим о кривых‚ заданных параметрически и не параметрически. Возвращаясь к урокам математики в школе‚ вспомним‚ что кривую в пространстве можно определить параметрически и не параметрически. В простейшем случае прямой линии на плоскости можно определить её двумя способами:
Непараметрически: y=ax+b
Параметрически: x=g(u); y=h(u)
Явное непараметрическое задание функции‚ указанное выше‚ кажется простым и удобным в использовании и иногда так оно и есть. Имея значение x‚ можно вычислить значение функции f‚ а вместе с тем и значение y. Однако‚ что получится‚ если мы имеем не прямую‚ а какую-то кривую‚ для которой по данному значению х можно несколько разных значений у‚ как показано на рис.1.1? Теперь становится понятным как подобное явное задание функции легко может сбить с толку компьютерную программу‚ для которой не допускается многозначимость. Чтобы избежать этой проблемы FastShip использует параметрическое задание функции‚ для которого х и у (а также и z для случая в пространстве) являются независимыми функциями некоторого параметра u. В данном случае ограничением для u является его монотоное возрастание или убывание при движении по участку кривой. Параметр u это просто математическое “изобретение” и в действительности не имеет физических свойств по отношению к кривой.
|
|
|
Хотя выгода от использования параметрического задания налицо‚ оно имеет и свои недостатки. Возвращаясь к приведённому выше примеру‚ первый недостаток заключается в следующем: чтобы оценить местоположение точки‚ лежащей на линии ‚в пространстве нужно использовать два уравнения‚ а не одно‚ как в случае явного задания прямой. Поэтому в вычислительном отношении параметрическое задание сложнее. Второе‚ мы часто хотим вычислить у по данному х или х по данному у и ничего не знать про параметр u. При параметрическом задании сперва вычисляется u по заданному х‚ а потом уже у. Это не всегда является кратчайшим путём.

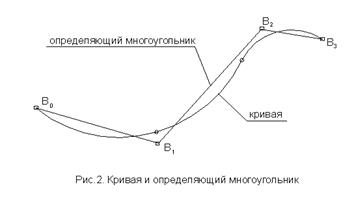
Продолжим рассмотрение других ключевых концепций. Рассмотрим кривую В-сплайн, показанную на рис.3.2.Сплошная линия представляет кривую, а пунктирная линия представляет определяющий многоугольник.
Определяющий многоугольник состоит из ряда вершин, обозначенных на рисунке B0 до B3, связанных отрезками прямых линий. Это и есть те вершины, по которым определяется действительная форма кривой. Как уже отмечалось ранее, кривая и определяющий многоугольник связаны набором функций полиномов, называемых базисными функциями В-сплайна.
Обратите внимание на сходство форм определяющего многоугольника и кривой. В некотором отношении определяющий многоугольник можно рассматривать как карикатуру или увеличенное изображение кривой, которую он определяет. Обретя небольшой опыт, вы сможете легко отличать В-сплайн от определяющего многоугольника. Кроме того, вершины - это ручки, которые позволяют пользователю управлять формой кривой. Управляя положениями вершин можно управлять формой кривой. Хотя это не совсем строго, иногда для начинающих пользователей полезно думать о кривой, как о присоединённой к вершинам магнитами.
Следующая концепция, которой нужно уделить внимание для полного рассмотрения математики NURBS, касается узлового вектора. Проще говоря, узловой вектор – это перечень значений параметра u, который служит для определения положения вершин определяющего многоугольника в параметрическом пространстве. Для кривой в примере 3.2 значения узлов обозначены кружочками на кривой. Имеется множество способов, которыми можно рассматривать значимость узлового вектора. Значения узлового вектора определяют границы интервалов кривой, то есть те места кривой, где заканчивается интервал одного многочлена и начинается интервал другого. Для В-сплайна четвертого порядка (кубического) на рис.3.2, часть кривой с левого края до первого внутреннего узла - кубическая кривая, в то время как часть от этого узла до следующего - совсем другая кубическая функция. И напоследок отметим ещё одну деталь. Зачастую вызывают затруднения термины порядок и степень кривой. В контексте нашего рассуждения, степень кривой - это самая высокая целая степень многочлена, задающего кривую. Порядок – это степень плюс один и происходит из того, что в простейшей функции многочлена типа f (x) = ax3 + bx2 + сх + d число неизвестных коэффициентов на одно больше, чем самая высокая степень многочлена, из-за того что постоянная d имеет нулевую степень. Следовательно, кубический В-сплайн имеет третью степень, но - четвертый порядок.
|
|
|
|
|
|


