 |
Лекция 5.Многокритериальные методы принятия управленческих решений.
|
|
|
|
1. Принятие управленческих решений в условиях полной определенности.
2. Принятие управленческих решений в условиях неопределенности и риска.
1. Принятие управленческих решений в условиях полной определенности.
Проблема управления деятельностью предприятия заключается в определении различных альтернатив действий и выборе оптимальной альтернативы, т. е. такой, которая позволяет получить наилучший результат в достижении поставленной цели.
В качестве альтернатив могут выступать новые целевые области (товарные рынки), виды выпускаемой продукции, инвестиции в различные сферы деятельности предприятия и т. д. Как правило, они не могут быть реализованы одновременно.
Целенаправленный выбор среди подобных альтернатив представляет собой принятие управленческого решения.
Реализация (осуществление) любой возможной альтернативы ведет к одному или нескольким последствиям (результатам). Ожидаемыми результатами могут быть выручка от реализации товаров, издержки производства, доля удовлетворения спроса, прибыль, затраты на продвижение товара, доля рынка и др.
На значение результата обычно оказывают влияние разнообразные факторы. Возможное положение дел, не зависящее напрямую от воздействия руководства предприятия, называется ситуацией внешней или окружающей среды. Состояние внешней среды складывается, как правило, в результате имеющейся политической обстановки (стабильная, нестабильная), поведения конкурирующих фирм (реактивное. нереактивное поведение), социально-экономических условий (платежеспособного спроса, правительственного регулирования экономики и т. д.). Состояния внешней среды в теории принятия решений называют обычно гипотезами.
|
|
|
Каждой реализуемой альтернативе 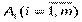 соответствуют некоторые состояния окружающей среды
соответствуют некоторые состояния окружающей среды 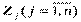 . Ожидаемый результат eij при выборе альтернативы Ai и принятии гипотезы Zj получается, если применить функцию предпочтения, или, как чаще всего говорят, функцию полезности f, т.е.:
. Ожидаемый результат eij при выборе альтернативы Ai и принятии гипотезы Zj получается, если применить функцию предпочтения, или, как чаще всего говорят, функцию полезности f, т.е.:
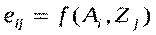
Значения функции f наглядно представляются в виде так называемой матрицы ожидаемых результатов. При этом могут задаваться вероятности появления ситуаций внешней среды (гипотез) 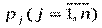 , которые при принятии решений считаются рисками.
, которые при принятии решений считаются рисками.
Таким образом, проблема принятия решения может быть сведена к получению необходимой информации, размещению ее в виде таблиц, например в виде табл. 1. представляющих собой по существу основные модели задач теории принятия решений, и выбору оптимальной альтернативы.
Таблица 1
Матрица описания задач принятия решений
| Альтернативы, Аi | Состояния внешней среды, Zj (гипотезы) | |||
| Z1 | Z2 | …. | Zn | |
| А1 | e11 | e12 | …. | e1n |
| А2 | e21 | e22 | …. | e1n |
| …. | …. | |||
| Аm | em1 | em2 | …. | e mn |
| Вероятности гипотез, pj | p1 | p2 | …. | Pn |
Здесь eij означает ожидаемый результат от применения альтернативы Ai при наступлении состояния внешней среды Zj.
Если в матрице решений имеется доминирующая альтернатива, то она и выбирается в качестве оптимального решения.
Однако, как правило, доминирующие альтернативы отсутствуют и, кроме того, решение приходится принимать в условиях риска и неопределенности. Здесь нужны специальные принципы принятия решений, или решающие правила, или критерии принятия решений, которые используются иногда как синонимы.
Ниже рассмотрим методы принятия решений:
а) в условиях полной определенности, когда известны все составляющие и характеристики проблемы управления;
б) в условиях вероятностной определенности (риска);
в) в условиях неопределенности.
|
|
|
Необходимо различать однокритериальные и многокритериальные методы выбора управленческих решений.
1. Однокритериальные методы выбора управленческих решений.
Считается известным:
• исходное множество альтернатив 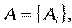
• оценки результатов выбираемых альтернатив f (Ai);
· критерий выбора 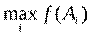 или
или 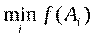 .
.
Следовательно, выбор характеризуется однозначной связью между принятым решением Ai и его результатом f (Ai). В процессе решения задачи определяется альтернатива A*, для которой f (A*)=max f (Ai) или f (A*)=min f (Ai).
2. Многокритериальные методы выбора управленческих решений.
В достаточно большом количестве практических случаев принятия решений при планировании действий приходится учитывать не один, а несколько критериев. Можно считать, что все критерии стремятся к максимуму, так как если некоторые критерии минимизируются, то путем умножения их на (-1) они будут стремиться к максимуму, причем решение при этом не изменяется.
Матрица исходных данных принятия решений имеет вид (табл. 2).
Таблица 2
Матрица исходных данных для многокритериальных методов выбора
| Альтернативы, Аi | Критерии (цели) | |||
| Z1 | Z2 | …. | Zn | |
| А1 | e11 | e12 | …. | e1n |
| А2 | e21 | e22 | …. | e1n |
| …. | …. | |||
| Аm | em1 | em2 | …. | e mn |
| Значимость критерия, αj | α1 | α2 | …. | αn |
В случае многокритериальной оптимизации возникают три проблемы.
Первая проблема связана с выбором принципа оптимальности. В математическом отношении эта проблема эквивалентна задаче упорядочения векторных множеств, а выбор принципа оптимальности - выбору отношений порядка.
Вторая проблема связана с нормализацией векторного критерия F(х). Дело в том, что частные критерии имеют различные единицы измерения, поэтому их необходимо привести к единому масштабу измерения, т. е. нормализовать(обычно приводят к безразличным величинам).
Третья проблема связана с учетом приоритета (степени важности) частных критериев. Часто для учета приоритета вводится вектор распределения важности или значимости критериев 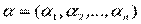 .
.
Рассмотрим методы многокритериальной оптимизации:
1. Метод равномерной оптимизации:
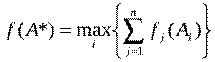 (1)
(1)
Он применяется, если глобальное качество альтернативы представляет собой сумму локальных (частных) качеств и, кроме того, все критерии имеют одну и ту же единицу измерения, например денежное выражение либо безразмерные величины. Главный недостаток метода -это возможность компенсации малых значений некоторых критериев достаточно большими значениями других.
|
|
|
2. Метод справедливого компромисса:
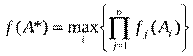 (2)
(2)
3. Метод свертывания критериев:
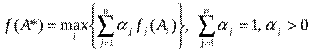 (3)
(3)
Здесь каждому из критериев приписываются весовые коэффициенты αj
4. Метод главного критерия:
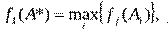 (4)
(4)
Здесь f 1(х) - главный (наиболее важный из всех) критерий.
5. Метод идеальной точки. Ищется план, удовлетворяющий условию:
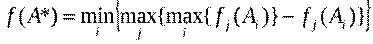 (5)
(5)
На первом этапе применяется м етод нормализации критериев (получение безразмерной формы критериев).
Так как критерии могут иметь различные масштабы и шкалы измерения, то прежде, чем приступить к решению многокритериальной задачи, их необходимо привести к одной единице измерения (обычно к безразмерному виду). Этот процесс называется нормализацией. Существуют различные методы нормализации, Предлагается следующий способ получения безразмерной формы критериев:
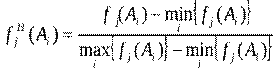 (6)
(6)
где 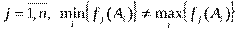
Рассмотрим пример многокритериальной задачи управления. Пусть фирма имеет возможность реализовывать свои товары на 4-х различных рынках (альтернативы А1, А2, А3, А4). При этом ставятся одновременно следующие цели: минимизация затрат на рекламу, завоевание максимальной доли рынка и максимальный объем продаж в течение планируемого периода. Исходные данные приведены в табл. 3.
Таблица 3
|
|
|


