 |
В8: Производная по графику
|
|
|
|
Задача В8
Производная по графику
На задаче В8 легко потерять балл… из-за невнимательности (например, график производной принимают за график функции) и незнания связи функции с касательной и производной. Незнание сейчас будем ликвидировать! А невнимательность оставлю на вашу совесть…
Прочитав и разобрав до конца урок по В8, ты узнаешь:
1) связь графика функции с касательной,
2) уравнение касательной к графику,
3) как схематично нарисовать график производной по графику функции,
4) как найти экстремумы на графике производной и на графике функции,
5) свойство параллельности и перпендикулярности двух прямых,
6) связь пути и скорости через производную.
Если всё это тебе известно, то ВСЁ РАВНО прочти урок и убедись, что знаешь!
Любой график имеет касательную (не одну!). Давайте вспомним их связь на небольшой схеме ниже:
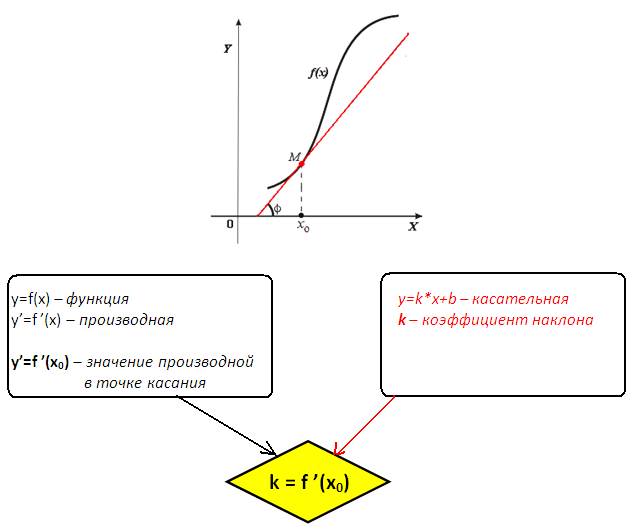
Из последней связи вытекает, что:
k = 0, если угол φ = 0. Значит на графике такие касательные будут в точках:
Пример задачи на вышесказанное:
Задача: На рисунке изображен график функции y = f(x), определенной на интервале (-1; 11). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = -20.
Решение:
По условию, касательная || (параллельна) к графику функции y = -20. А y = -20 – это прямая || оси Х, следовательно касательная к графику имеет нулевой угол наклона, т.е. k = 0/
Чтобы составить уравнение касательной, зная толь0ко функциюЗ y=f (x) и точку касания x0, существует алгоритм:
1) y’=f ’(x) – найти производную функции;
2) y’=f ’(x0) – вычислить значение производной в точке касания;
3) y=f (x0) – вычислить значение функции в этой точке;
4) y=f ’(x0)*(х – x0) + f (x0) – уравнение касательной.
Про касательную вспомнили. Она нам понадобится при решении задач.
|
|
|
Функция y возрастает, если производная y’>0
Функция y убывает, если производная y’<0
Покажем соответствие на графиках:
Таким образом, зная один из графиков, всегда можно представить другой. Т.е. по графику производной можно найти промежутки возрастания и убывания функции.
Экстремумы можно найти на любом графике… и на гр.функции и на гр.производной.
т. max – точка в которой производная меняет знак с «+» на «−»,
т. min – точка в которой производная меняет знак с «−» на «+».
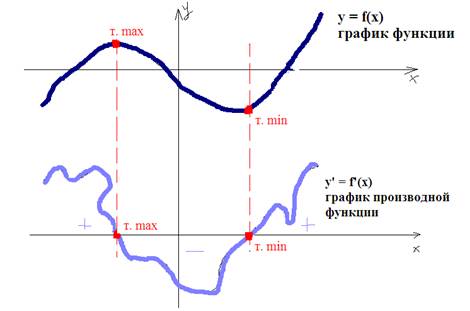
Заметили? Что на графике функции экстремумы лежат на «вершинках» и в «ямочках». На «вершинках» - т.max, в «ямочках» – т.min.
А на графике производной экстремумы лежат на оси Х, в точках пересечения графика с осью Х (в точках смены знака производной).
S’(t) = v(t). Т.е. производная пути = скорости. И Путь и Скорость – это функции, зависящие от времени.
В задачах, вместо S часто пишут Х.
Например,
Материальная точка движется прямолинейно по закону 
, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 1 с.
Решение:
V(t) = X’(t) = t – нашли зависимость скорости от времени
V(1) = 1 – нашли скорость в момент времени t=1.
Ответ: 1
Ещё одна важность: свойства параллельности и перпендикулярности прямых:
Две прямые y = k1*x + b1 и y = k2*x + b2 параллельны, если k1 = k2.
Две прямые y = k1*x + b1 и y = k2*x + b2 перпендикулярны, если k1*k2 = -1
Задача:
На рисунке изображен график y=f’(x) — производной функции f(x), определенной на интервале (–6; 7). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = –x –20 или совпадает с ней.
Решение:
Мы знаем, что f ‘(xo) = k.
По условию касательная y = f ‘(xo)·x + b должна быть параллельна прямой y = –x –20. Значит f ‘(xo) = –1
На рисунке изображен график производной. А нам нужны те точки, в которых производная равна –1. Такие точки отмечены красным:
|
|
|
Ответ: 3
Если остались недопонимания – запишись на бесплатную консультацию.. ЧТО, КАК и ГДЕ это будет – читай ЗДЕСЬ.
yandex_partner_id = 89284; yandex_site_bg_color = 'FFFFFF'; yandex_site_charset = 'utf-8'; yandex_ad_format = 'direct'; yandex_direct_type = '600x60'; yandex_direct_header_position = 'bottom'; yandex_direct_title_color = '993300'; yandex_direct_url_color = '993300'; yandex_direct_all_color = '666666'; yandex_direct_text_color = '000000'; yandex_direct_hover_color = 'FF6600'; yandex_direct_favicon = false; document.write('');
_
yandex_partner_id = 89284; yandex_site_bg_color = 'FFFFFF'; yandex_site_charset = 'utf-8'; yandex_ad_format = 'direct'; yandex_direct_type = '728x90'; yandex_direct_header_position = 'bottom'; yandex_direct_title_color = '993300'; yandex_direct_url_color = '993300'; yandex_direct_all_color = '000000'; yandex_direct_text_color = '000000'; yandex_direct_hover_color = 'FF6600'; yandex_direct_favicon = false; document.write(''); Нажмите, чтобы отменить ответ.
Добавить рекламную строку
|
|
|
