Примеры решения задач по теме 3

«Электростатика и постоянный ток»

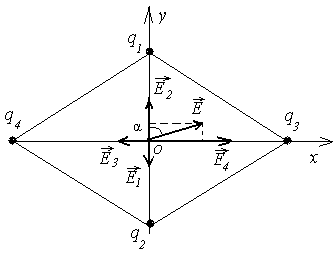
Задача 1 Диагонали ромба имеют длину d₁ = 2 см, d₂ = 3 см. На концах короткой диагонали расположены заряды q₁ = 2 нКл, q₂ = 6 нКл; на концах длинной - заряды q₃ = 3 нКл, q₄ = 12 нКл. Определить модуль вектора напряженности электрического поля в центре ромба и угол между вектором напряженности и короткой диагональю.

Дано:

d1 = 2 см d2 = 3 см q1 = 2 нКл q2 = 6 нКл q3 = 3 нКл q4 = 12 нКл	Решение
E, a -?

 

Так как электрическое поле создано несколькими зарядами, то для нахождения его напряженности надо применить принцип суперпозиции. Напряженность результирующего поля равна векторной сумме напряженностей полей, созданных каждым зарядом в отдельности:

.

Направления векторов показаны на рисунке. Модули составляющих векторов можно найти по формуле напряженности поля точечного заряда:

 

 

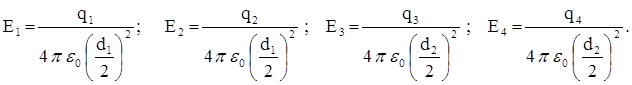
Чтобы сложить вектора, выберем координатные оси х и у, как показано на рисунке, и найдем проекции результирующего вектора E_x и E_y как суммы проекций всех составляющих векторов на эти оси координат:

 

 

Здесь Е_1х = - Е₁, Е_2х = Е₂, Е_3х = 0, Е_4х = 0,

 

Е_1у = 0, Е_2у = 0, Е_3у = - Е₃, Е_4у = Е₄.

 

Тогда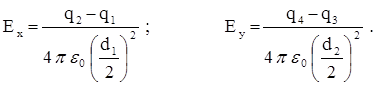

Вычислим проекции вектора :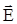

 

 

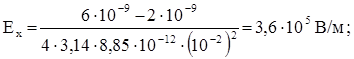
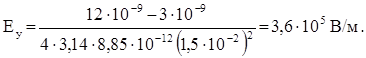
Модуль результирующего вектора Е найдем через его проекции на оси координат:

 

Найдем теперь угол, который вектор 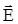образует с короткой диагональю ромба. Из рисунка видно, что 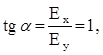значит a = 45^о.

 

Ответ: Е = 5,09×10⁵ В/м, a = 45^о.

 

 

Задача 2 Тонкий стержень длиной l = 10 см заряжен с линейной плотностью t = 400 нКл/м. Найти напряженность электрического поля в точке, расположенной на перпендикуляре к стержню, проведенном через один из его концов, на расстоянии r₀ = 8 см от его конца.

 

Дано:

l = 10 см t = 400 нКл/м r0 = 8 см	Рис.1.6 Решение   Применим принцип суперпозиции для поля непрерывно распределенных зарядов: .
Е -?

 

 

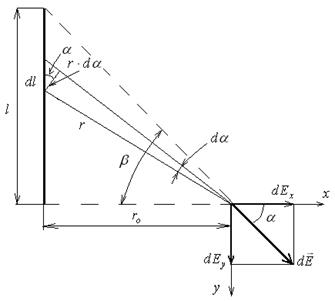
Выделим на стержне бесконечно малый участок длиной d l (рис.1.6) Находящийся на нем заряд 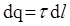можно считать точечным, и напряженность поля, созданного им, рассчитывать как

.

 

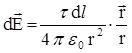Из приведенного рисунка видно, что

Следует иметь в виду, что 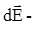вектор, поэтому прежде чем интегрировать, выберем оси координат х и y и найдем проекции вектора на эти оси:

 

,

 

или, учитывая сделанные подстановки,

 

Интегрируя эти выражения в пределах от 0 до b (рис. 1.6.), получим:

 

где Е_х и Е_у – проекции результирующего вектора на оси х и у.

Подставим числовые значения заданных величин в системе СИ и произведем вычисления:

 

 

 

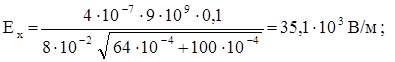
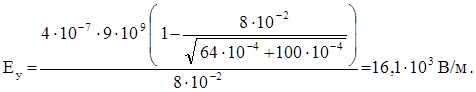
Вектор напряженности определится через проекции Е_х и Е_у:

 

 

где – орты координатных осей х и у.

Модуль вектора напряженности найдем через его проекции на оси координат:

 

.

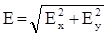Вычислим:

 

Ответ: Е = 39,3×10³ В/м.

 

 

Задача 3 Эбонитовый сплошной шар (диэлектрическая проницаемость e = 3) радиуса R = 5 см несет заряд, равномерно распределенный с объемной плотностью r = 10 нКл/м³. Определить напряженность электрического поля в точках: 1) на расстоянии r₁ = 3 см от центра шара; 2) на поверхности шара; 3) на расстоянии r₃ = 10 см от центра шара. Построить график зависимости Е(r).

 

Дано:

e = 3 r = 10 нКл/м3 r1 = 3 см r2 = R r3 = 10см	Решение   Применим метод Гаусса. Теорему Гаусса надо применять для вектора электрического смещения 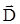, так как в этом случае достаточно учесть только дополнительные (свободные) заряды, сообщенные диэлектрику извне и не надо рассматривать связанные поляризационные заряды диэлектрика.
Еr1, ЕR, Er2 -?

Ввиду сферически симметричного распределения свободного заряда есть основание утверждать, что линии вектора 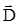в любой точке направлены вдоль радиусов, проведенных из центра шара, и модуль D имеет одинаковое значение на равных расстояниях от центра шара. Следовательно, в качестве гауссовых поверхностей следует выбирать сферы радиуса r с центром, совпадающим с центром шара (см. рисунок).

Рассмотрим две области пространства:

1. 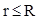. Поток вектора электрического смещения через гауссову сферу равен

 

.

Свободный заряд, попавший внутрь этой сферы, равен .

По теореме Гаусса 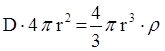, отсюда

.

 

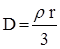Так как диэлектрик заполняет пространство между двумя эквипотенциальными поверхностями, то связь между 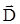и 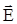имеет вид

.

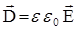Тогда модуль напряженности электрического поля равен .

2. . Поток вектора электрического смещения через сферу радиуса r, как и в предыдущем случае, равен .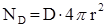

 

Свободный заряд, попавший внутрь этой сферы с r > R – это весь заряд шара:

.

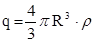По теореме Гаусса 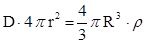, отсюда

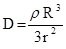, а напряженность поля в этой области , так как e = 1.

Получим .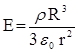

 

Теперь можно построить график зависимости E(r).

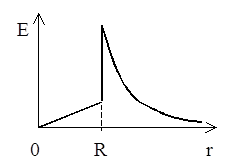
Отметим, что на границе перехода поля из эбонита в воздух происходит скачок напряженности в e раз.

Вычислим значения напряженности в нужных точках:

1) r₁ = 3 см. .

2) r₂ = R. Напряженность имеет два значения:

 

а) внутри шара ;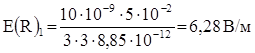

 

б) вне шара .

3) r₃ = 10 см. .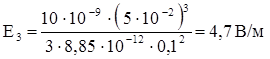

 

Ответ: Е₁ = 3,37 В/м; Е(R)₁ = 6,28 В/м, Е(R)₂ = 18,8 В/м; Е₃ = 4,7 В/м.

 

Задача 4 Пространство между пластинами плоского конденсатора заполнено диэлектриком. Расстояние между пластинами d = 2 мм. На пластины подана разность потенциалов U₁ = 600 В. Если, отключив источник напряжения, вынуть диэлектрик из конденсатора, то разность потенциалов на пластинах возрастет до U₂ = 1800 В. Найти поверхностную плотность связанных зарядов на диэлектрике σ_св и диэлектрическую восприимчивость κ диэлектрика.

 

Дано:

d = 2 мм U1 = 600 В U2 = 1800 В	Решение   Так как конденсатор после зарядки отключили от источника напряжения, то величина заряда на его обкладках остается постоянной. Заряд конденсатора связан с его емкостью и разностью потенциалов соотношением q = CU, поэтому можно записать, что С1U1 = C2U2.
σсв, κ -?

 

Здесь - емкость конденсатора с диэлектриком,

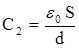- емкость конденсатора без диэлектрика.

Тогда получается, что диэлектрическая проницаемость диэлектрика ε равна

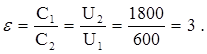
Но диэлектрическая восприимчивость связана с диэлектрической проницаемостью соотношением κ = ε – 1, то есть κ = 2.

Известно, что поверхностная плотность связанных зарядов на диэлектрике равна проекции вектора поляризации на внешнюю нормаль к поверхности диэлектрика. В плоском конденсаторе вектор поляризации перпендикулярен поверхности диэлектрика, поэтому σ_св = Р.

В однородных изотропных диэлектриках вектор поляризации пропорционален напряженности поля P = κ ε₀ E.

Напряженность электрического поля в диэлектрике легко найти, так как поле плоского конденсатора является однородным: 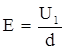. Тогда выражение для поверхностной плотности связанных зарядов диэлектрика примет вид

.

Вычислим

 

Ответ: κ = 2, σ_св = 5,3·10^-6 Кл/м².

 

Задача 5 Электрон влетает в поле плоского конденсатора со скоростью v₀ = 1 Мм/с под углом α = 30^о к его пластинам. Длина пластин l = 5 см. Найти напряженность поля, при которой скорость электрона при вылете из конденсатора будет направлена параллельно его пластинам.

 

Дано:

α = 30о l = 5 см |q| = 1,6·10-19 Кл m = 9,1·10-31 кг v0 = 1 Мм/с	Решение   Поле плоского конденсатора является однородным, поэтому на электрон в этом поле будет действовать постоянная сила, а значит, движение электрона будет равноускоренным. Для описания этого движения выберем начало координат в точке влета электрона, направим ось х вдоль пластин, а ось у – перпендикулярно им.
E -?

Тогда закон движения электрона примет вид 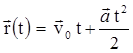. Скорость электрона при этом равна . Запишем эти уравнения в проекциях на выбранные оси координат:

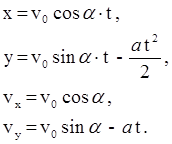
Так как в точке вылета x = l, то , а так как электрон вылетает параллельно пластинам, то в точке вылета v_y = 0, тогда . Отсюда

 

.

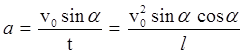По второму закону Ньютона 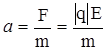, отсюда .

 

 

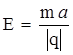Тогда окончательно получаем

.

 

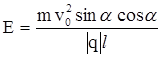Вычислим напряженность поля: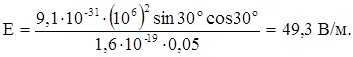

 

Ответ: Е = 49,3 В/м.

 

 

Задача 6 Электрический заряд распределен в вакууме по объему шара радиусом R = 10 см. Объемная плотность заряда внутри шара изменяется по закону ρ = ρ₀·r, где ρ₀ = 1 мКл/м³. Найти энергию электрического поля, заключенную в шаре.

 

Дано:

R = 10 см ρ0 = 1 мКл/м3	Решение Чтобы найти энергию электрического поля в некотором объеме, надо знать объемную плотность энергии, а для этого, в свою очередь, надо знать напряженность электрического поля.
W -?

 

Так как по условию заряд распределен в пространстве сферически симметрично, то для нахождения напряженности поля надо применить теорему Гаусса. Выберем гауссову поверхность в виде сферы радиуса r < R (см. рисунок). Силовые линии электрического поля в любой точке сферы будут перпендикулярны к ней, а модуль напряженности во всех точках сферы будет одинаков. Тогда поток вектора напряженности через поверхность сферы равен

.

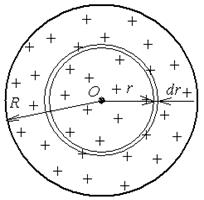
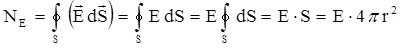Заряд, попавший внутрь этой сферы, надо искать интегрированием: 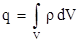, при этом, так как ρ зависит только от r, элемент объема dV – это объем сферического слоя радиусом r и толщиной dr, то есть dV = 4 π r²dr. Тогда заряд q равен .

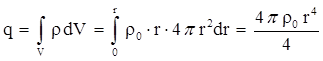Используем теорему Гаусса, приравнивая поток вектора напряженности через поверхность S суммарному заряду внутри этой поверхности, деленному на электрическую постоянную ε₀:

.

Выразим отсюда напряженность электрического поля Е: .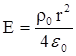

Теперь найдем объемную плотность энергии электрического поля внутри шара:

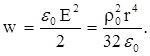
И, наконец, найдем энергию электрического поля, заключенную в шаре:

Вычислим значение энергии:

 

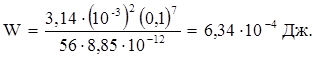
Ответ: W = 6,34·10^-4 Дж.

 

 

Задача 7 Сила тока в проводнике изменяется за время от t₁ = 3 c до t₂ = 7 с по закону I = At² + B, где А = 0,1 А/с², В = 2 А. Определите заряд, прошедший по проводнику.

Дано:

I = At2 + B А = 0,1 А/с2 В = 2 А t1 = 3 c t2 = 7 с	Решение По определению сила тока равна ,
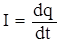q –?

 

отсюда .

Полный заряд, прошедший по проводнику за время от t₁ = 3 c до t₂ = 7 с, равно

 

.

 

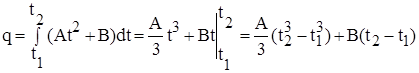Произведем вычисления:

 

Ответ: q = 18,5 Кл.

 

Задача 8 Источник тока с ЭДС замкнут на реостат. При силе тока I₁ = 0,2 А и I₂ = 2,4 А на реостате выделяется одинаковая мощность. Найти:

1. При какой силе тока на реостате выделяется максимальная мощность?

2. Чему равна сила тока короткого замыкания?

 

Дано:

I1 = 0,2 А I2 = 2,4 А P1 = P2	Решение При силе тока I1 на реостате выделяется мощность 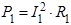, при силе тока I2:
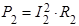
I –? Iкз –?

где R₁ и R₂ – сопротивления реостата в каждом случае. По условию P₁ = P₂, поэтому:

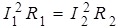. (1)

По закону Ома для полной цепи:

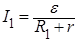, (2)

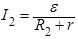. (3)

Из (2) и (3) выражаем R₁ и R₂:

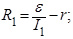
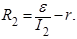
Подставив в (1) получаем:

.

Отсюда находим отношение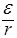

;

.

Максимальная мощность выделяется при условии R = r, при этом ток равен

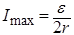. (4)

Ток короткого замыкания:

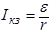. (5)

 

Произведем вычисления:

; .

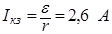Ответ:I = 1,3 А;. I_кз = 2,6 А.

 

 

Поделиться:

Воспользуйтесь поиском по сайту: