 |
III. Одночастевая математическая модель фармакокинетики
|
|
|
|
а) Метод однократного введения препарата в орган

Рис. 1
Терапевтический эффект препарата зависит от его концентрации и времени пребывания в действующей концентрации. Изменение концентрации dL препарата в органе пропорционально его концентрации L и промежутку времени, за который происходит изменение:
dL= – B×L×dt, (1)
где B - коэффициент скорости выведения препарата из органа. Решение этого уравнения имеет вид убывающей экспоненты L(t) = L0×exp(–Bt) (L0 – начальная концентрация), график которой представлен кривой 1 на рис.2.
б) Метод непрерывного введения препарата
Дифференциальное уравнение такой системы (см.рис.1):
dL/dt = QN – B×L, (2)
где QN - скорость введения препарата.
Решение уравнения (2) имеет вид возрастающей экспоненты (кривая 2, рис.2).
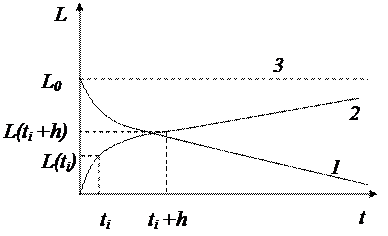 |
Рис. 2
Сочетанием двух методов введения, а) и б) меняя Q, можно достичь постоянной концентрации препарата в органе (кривая 3, рис.2), что часто необходимо на практике. Данные рис. 2 подтверждены экспериментально.
II. Двухчастевая модель непрерывной инфузии в кровь
 |
Рис. 3
В этой структурной схеме:
QN - скорость непрерывного введения препарата в кровь,
К - концентрация препарата в крови,
А - коэффициент скорости выведения препарата из крови в орган,
B - коэффициент скорости выведения препарата из органа в кровь,
G - коэффициент удаления препарата из крови почками.
Скорость изменения концентрации препарата в крови равна:
dK/dt = – AK+BL – GK+QN. (3)
Скорость изменения препарата в органе:
dL/dt = AK – BL. (4)
Система уравнений (3)-(4) решается наиболее просто численным методом Эйлера. Величину скорости изменения концентрации препарата в органе приближенно можно вычислить как отношение приращения L(ti+h)-L(ti) концентрации препарата к промежутку времени h, за который оно произошло (см. рис.2):
|
|
|
dL(ti)/dt» (L(ti+h) – L(ti))/h. (5)
В пределе при h-->0 выражение (5) в точности выполняется. Найдем из уравнения (5):
L(ti+h)» L (ti)+h(dL(ti)/dt). (6)
Подставив уравнение (4) в (6) получим:
L(ti+h)» L(ti)+h[AK(ti)– BL(ti)] (7)
Аналогично выводится формула для вычислений K(ti+h):
K(ti+h)» K(ti)+h[QN+BL(ti)-AK(ti)-GK(ti)] (8)
По формулам (7) и (8) и осуществляется расчет. Как видно из уравнений (7) и (8), для подсчета L(ti+h), K(ti+h) необходимо знать предыдущие значения L(ti), K(ti) и задаться шагом по оси времени h. При различных сочетаниях значений индивидуальных коэффициентов A, B, G решение системы уравнений (7) и (8) приводит к различным вариантам зависимости L(t), K(t) при разных значениях Q0 и QN.
Рассмотренные модели фармакокинетики позволяют рассчитать и подобрать оптимальную схему дозирования лекарственного препарата. Оптимальной является схема, удовлетворяющая следующим условиям:
1. Концентрация препарата в крови или органе больного после первичного приема должна достаточно быстро достигать уровня, не ниже эффективного, терапевтического значения Стер, а между приемами препарата, не стать меньше этой величины.
2. Максимальная концентрация препарата в крови или органе не должна быть больше предельной концентрации Сдоп.
Таким образом, оптимальная концентрация препарата должна быть в пределах:
Стер < Сопт < Сдоп.
Если С< Стер, то препарат мало активен или не активен, если С > Сдоп, то будет высока вероятность возникновения токсических явлений.
Порядок выполнения работы
Для всех способов введения. Введите исходные данные в соответствии с Вашим вариантом задания: индивидуальные коэффициенты больного A, B, G, его массу М (в кг), Kдоп и Kте р – максимально допустимое и минимальное терапевтическое значения концентрации препарата в крови (в мг/л), Т – время наблюдения (в часах).
|
|
|
Примечание1. Значения максимально допустимой и минимальной терапевтической концентрации препарата в органе рассчитываются в программе по формулам для стационарного состояния:  и
и  . Эти значения запишите, когда будете смотреть график L(t).
. Эти значения запишите, когда будете смотреть график L(t).
Примечание2. В программе предполагается, что начальные концентрации препарата в крови и органе равны нулю: К(0) = L(0) =0.
|
|
|


