Главная | Обратная связь | Поможем написать вашу работу!

Турбомолекулярные насосы с подшипниками KYKY (Китай)

Характеристики		FF-100/110E	FF-160/700E	FF-160/700FE	FF-200/1300E	FF-200/1300FE	FF-250/2000E
Быстрота действия, л/с		150	700	700	1300	1300	2000
Степень сжатия	N₂	10⁸	10⁹	10⁹	10⁹	10⁹	10⁹
	H₂	5х10²	6х10⁶	6х10⁶	6х10³	6х10³	6х10³
Предельный вакуум, не хуже, Па	ISO	4.5х10^-⁷	6х10^-⁷	6х10^-⁷	6х10^-⁶	6х10^-⁶	6х10^-⁶
	CF	4.5х10^-⁸	6х10^-⁸	6х10^-⁸	6х10^-⁷	6х10^-⁷	-
Вх. фланец, Ду, мм.		ISO100	ISO160	ISO160	ISO200	ISO200	ISO250
Вых. фланец, Ду, мм.		KF25	KF40	KF40	KF40	KF40	KF50
Положение монтажа		любое
Охлаждение		вода-воздух	вода	вода-воздух	вода	вода-воздух	вода

Криосорбционные вакуумные насосы SICERA ™ Cryopump

При мощности всего 0,9кВт, благодаря запатентованной инверторной технологии, насосы серии SICERA меняют определение «низкое потребление энергии», уменьшая Ваши затраты на электроэнергию на 20-30%. Качественно новая система позволяет одновременно использовать до шести насосов (200 мм) на одном компрессоре без уменьшения производительности.

Насосы серии SICERA доступны с размерами фланцев 200 и 300 мм, обе модели имеют полностью автоматический цикл регенерации, что позволяет максимизировать время продуктивной работы. В результате, экономия электроэнергии и увеличенная производственная эффективность делают насосы данной серии идеальными для таких применений как массовое производство полупроводниковых пластин, плоскопанельных дисплеев и прочих схожих производств.

Технические характеристики

Модель		CP-8	CP-8LP	CP-250LP	CP-12	CP-16	CP-20	SICERA 8»	SICERA 12»
Скорость откачки (л/сек)	Воздух	1500	1800	3060	3600	4800	9700	1500	3300
	Вода	4200	4200	6300	9560	17300	29100	4000	9500
	Аргон	1250	1500	2500	3100	4100	8300	1200	2700
	Водород	2300	3000	5000	7300	12000	14000	2200	6000
Пропускная способность	Аргон (тор-л/сек)	11.0	11.0	11.0	12.6	11.4	11.3	8.9	8.9
	Аргон (см3/ мин)	870	870	870	1000	900	900	700	700
Емкость (стандартные литры)	Аргон при 1x10-6 торp	1200	1600	1600	3100	5500	6000	1000	2000
	Водород при 5x10-6 торp	25	25	25	50	50	33	12	30
Параметр включения в работу (торр-литры)	-	220	220	220	650	500	400	150	150
Время захолаживания (мин)	-	75	110	110	90	135	190	120	150
Входной фланец	ANSI	6»	6»	-	10»	-	20»	-	-
	ISO	200 мм	200 мм	250 мм	320 мм	400 мм	500 мм	-	-
	Conflat	10»	10»	-	-	-	-	253	-
	CVC	-	-	-	10»	10»	-	-	-

Криогенные вакуумные насосы CTI Cryogenics (США)

Крионасос/характеристики	CryoTorr 4F*	CryoTorr 8 и 8F*	CryoTorr 250F*	CryoTorr 10 и 10F*	CryoTorr 400	CryoTorr 20HP
Ду фланца, мм	100	200	250	320	400	500
Скорость откачки, л/сек
По азоту	370	1500	2200	3000	6000	10 000
По парам воды	1100	4000	6500	9000	16000	31500
По водороду	370	2500	3200	5000	5000	15000
По аргону	310	1200	1800	2500	5000	8400
Емкость по Аргону, ст. л.	210	1000	1000	2000	2500	5700
Емкость по Водороду, ст. л.	3	17	16	24	15	46
Время захолаживания, мин. (при 50 Гц)	90	110	120	120	180	150

Криогенные вакуумные насосы Oxford Instrument (Англия)

Модель крионасоса	Cryo-Plex 8LP	Cryo-Plex 8	Cryo-Plex 10	Cryo-Plex 16
Скорость откачки (л/с):
По парам воды	4000	4000	9000	16000
По воздуху	1500	1500	3000	5000
По водороду	2200	2500	5000	5000
По аргону	1200	1200	2500	4200
Производительность при 5x10^-6 Torr (ст. л/мин):
По водороду	12	18	24	15
По аргону	1000	1000	2000	2500
Максимальная газовая нагрузка:
По аргону (ст. л/мин)	700	700	1,500	500
Время охлаждения	90 мин	90 мин	60 мин	150 мин
Габариты:
Высота (мм)	179	526	607	610
Масса (кг)	20	21	39	72
Входной фланец	ANSI/ISO/CF DN200	ANSI/ISO/CF DN200	ANSI/ISO/CF DN320	ISO/CVC DN400

Проницаемость

Проникновение газа сквозь стенки сосуда является следствием растворения и диффузии газа, описываемых уравнениями:

(Коэффициент диффузии газа экспоненциально зависит от температуры материала)

(где u = 1, 1/2, 1/3,… в зависимости от количества атомов в молекуле.)

Количество газа, протекающего через 1 см² поверхности стенки единичной толщины в течение 1 с, т.е. удельный поток I1, зависит от коэффициента диффузии D, коэффициента растворимости r и от давлений по обе стороны стенки. Зависимость потока от давления более сложна, чем в случае течения свободного газа.

При растворении происходит диссоциация газа, зависящая от количества атомов в молекуле. В связи с этим поток газа сквозь стенку пропорционален разности давлений в степени u, т.е. рu₂-pu₁ - причем здесь верны те же критерии, что и при растворении.

Если внутри вакуумной системы давление низкое, а снаружи атмосферное, то диффузия со стороны атмосферы растворяющегося в стенках газа может привести к проникновению некоторых атмосферных газов внутрь вакуумной системы. Это натекание газа может быть количественно определено некоторым потоком натекания.

Установившееся течение. Предположим, что по одну сторону стенки площадью 1 см² и толщиной L имеется давление р1 а по другую - давление p2. Согласно уравнению (3.54), объемные концентрации газа на обеих поверхностях будут соответственно

Показатель степени и может иметь значение 1, 1/2 и т.д. в зависимости от свойств газа и характеристик материала стенки. При p2> p1 диффузия происходит от поверхности 2 к поверхности 1. Поток, соответствующий этой диффузии, находится из закона Фика:

Уравнение (3 59) можно проинтегрировать в соответствующих пределах, принимая D = const, а также I1= const в установившемся потоке:

Подставляя выражения (3.58) для nr1 и nr2 получим

Таким образом, удельный поток I1 возрастает вместе с увеличением перепада давлений по обе стороны стенки и уменьшается при увеличении ее толщины; он пропорционален произведению коэффициентов диффузии и растворимости газа в материале стенки.

Произведение коэффициентов растворимости r и диффузии D называется коэффициентом проникания:

Кривые, представленные на фиг. 3.21, показывают зависимость коэффициента проникания от температуры для некоторых двухатомных газов в металлах (u= 1/2), а также для некоторых одно- и двухатомных газов в стеклах и керамиках (u = 1).

Как видно из кривых, в целом проникновение газов через металлы больше, чем через стекло

Проницаемость органических веществ (пластмасс, эластомеров и т.п.) относительно велика. Для большинства этих материалов коэффициенты проникания различных газов (особенно легко ожижаемых газов типа СО2, NН3) имеют большие значения.

В табл. 3.15 приведены значения коэффициента проникания некоторых газов в различных металлах при комнатной температуре.

Предположим, что масса материала стенки равномерно насыщена газом при давлении р₀, а начальная объемная концентрация этого газа равна nr0. Когда давление над поверхностью стенки снизится до уровня р (р<<р₀), начнется десорбция с поверхности и переход газа в объем сосуда; его место будет занимать газ, диффундирующий из глубины материала к поверхности. Очевидно, что тут же у поверхности (при х = 0) возникнет градиент концентрации. При этом интенсивность газовыделения с поверхности можно описать формулой:

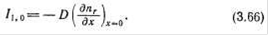
По мере газовыделения с поверхности стенки изменяется пространственное и временное распределения его концентрации в глубине материала. Такое состояние описывается вторым законом Фика:

При условии D = const это уравнение может быть записано в виде

Решение уравнения (3.676) дает поток газовыделения с единицы поверхности очень толстой стенки в момент т (отсчитываемый с момента начала понижения давления):

Таким образом, I1т имеет максимальное значение в момент т = 0 и уменьшается со временем. Теоретически при х = 0 I1т = ∞, что означает мгновенную десорбцию поверхностного слоя газа. Общее количество газа, истекающего с единицы поверхности за время т, определяется интегралом

Уравнения (3.68) и (3.69) справедливы также для случая, когда диффузия газа происходит из окружающей среды внутрь тела, в котором имеется газ с начальной концентрацией nr0, много меньшей концентрации окружающего воздуха. Тогда удельный поток I1 направлен внутрь твердого тела.

⇐ Предыдущая 1 23

Воспользуйтесь поиском по сайту: