 |
Практическое занятие 12. Изгиб пластинки по методу Ритца – Тимошенко.
|
|
|
|
Рассмотрим изгиб прямоугольной пластинки, шарнирно опертой по контуру и нагруженной равномерно распределенной нагрузкой q. Приближенное выражение функции прогибов выбираем в виде ряда
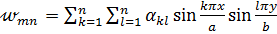(а)
где функции
,
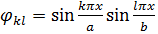как было показано в решении Навье курса ТУ, удовлетворяют всем граничным условиям шарнирного опирания пластинки – и геометрическим, и статическим.
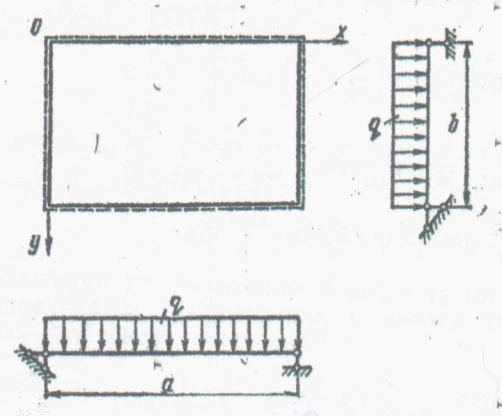
Рис.1
Для определения коэффициентов 
подсчитаем потенциальную энергию системы Э=U – A, ф.(7.2.2) лк. 7.
Потенциальная энергия U, накапливаемая при изгибе прямоугольной шарнирно опертой по контуру пластинки, может быть определена по ф.(7.2.3б) лк.7.
Подсчитаем оператор Лапласа над функцией 
:
,
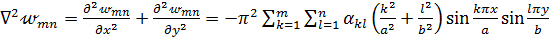и подставим это выражение в ф. (7.2.3б) лк. 7:
U= 
2dxdy,
где D – цилиндрическая жесткость пластинки: D=Eh3/12(1-μ2).
Получим
. (б)
Возведение в квадрат двойного ряда, стоящего под интегралом в квадратных скобках, равносильно перемножению двух многочленов, где каждый член первого ряда умножается на каждый член второго ряда. Чтобы отличить члены одного ряда от членов другого ряда, в одном из них индексы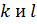 
заменим соответственно на 
. Тогда выражение, стоящее в квадратных скобках под интегралом в формуле (б), сведется к четверному ряду, который подставим в формулу (б); меняя порядок интегрирования и суммирования и вынося постоянные величины за знак интеграла, получаем: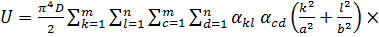 
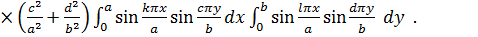(в)
Подсчитаем входящие сюда интегралы. Первый из них равен:
.
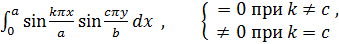Следовательно, рассматриваемый интеграл отличен от нуля только при 
; этот интеграл равен
. (*)
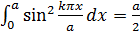Рассматривая второй интеграл в формуле (в), аналогично первому получаем:
. (г)
Подставляя полученные значения интегралов (*) и (г) в формулу (в) и учитывая, что они отличны от нуля только при значениях индексов суммирования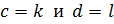 
, находим:
|
|
|
(**)
Работу внешних сил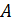 
при изгибе пластинки под действием поперечной нагрузки можно подсчитать по формуле (7.2.4) лк. 7:
.
Подставим в эту формулу функцию прогибов 
(а) и учтем, что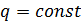 
:
.
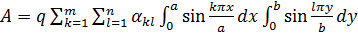Интегрируя, получаем:
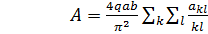
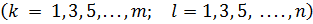. (д)
Подставим соотношения (**) и (д) в ф. (7.2.2) лк. 7, сохраняя в том и другом ряду только члены, содержащие нечетные индексы 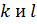(четные индексы дадут значения коэффициентов 
):
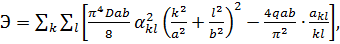
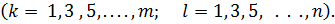
Коэффициенты нужно выбирать так, чтобы потенциальная энергия системы имела минимум, а значит должны выполняться условия (7.2.6) лк. 7. Вычисляя производные полученной функции Э по и приравнивая их к нулю, находим:
,
.
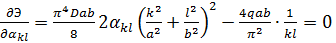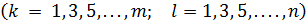После деления на величину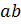 
, получаем следующую систему уравнений для определения постоянных :
,
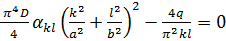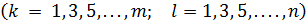
откуда находим значения постоянных коэффициентов ряда (а):
.
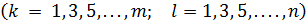
Подставим эти коэффициенты в уравнение погибов (а) и вынесем за знак суммы постоянный множитель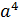 
:
. (е)
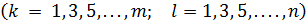
Если в формуле (е) взять бесконечно большое число членов, т. е. положить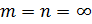 
, то получим решение задачи, совпадающее с точным решением Навье.
Возьмем приближенное решение, ограничиваясь одним членом ряда. Тогда из формулы (е) имеем:
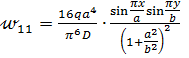. (ж)
Максимальный прогиб возникает в центре пластинки при x=a/2 и y=b/2, где он равен:
.
В случае квадратной пластинки, когда a/b=1, максимальный прогиб равен:
.
Подставляя в это соотношение выражение цилиндрической жесткости D и принимая коэффициент Пуассона μ 
, находим:
.
Это приближение отличается от точного, равного
,
всего на 2,7% в большую сторону.
Погонные изгибающие моменты найдем по формулам теории изгиба пластинок. Подставляя в эти формулы функции прогибов в первом приближении (ж), получаем:
,
.
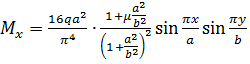Максимальные изгибающие моменты возникают в центре пластинки при 
и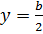 
, где они равны:
,
.
В случае квадратной пластинки, т. е. при отношении сторон 
, находим:
|
|
|
Точное значение максимальных изгибающих моментов для квадратной пластинки, приводимое в справочниках, равно:
Следовательно, максимальный изгибающий момент для квадратной пластинки, подсчитанный в первом приближении, отличается от точного значения на 11,7 %. Поэтому при вычислении изгибающих моментов в рассматриваемой пластинке следует брать еще несколько членов ряда (е). Еще менее точный результат получается при вычислении в первом приближении погонных поперечных сил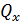 
и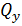 
.
|
|
|
