 |
Найдите параметр С и математическое ожидание.
|
|
|
|
В урне 4 белых и 7 чёрных шаров. Из урны случайным образом вынимают сразу 2 шара. Найти вероятность того, что оба шара белые.
Число N всевозможных исходов – выбор 2 шаров из 4+7=11 шаров – равно числу сочетаний из 11 по 2:

Число n исходов, благоприятствующих наступлению события А – из урны извлечено 2 белых шара, – это число сочетаний из 4 по 2:

Вероятность события А:

Прибор состоит из 5-ти последовательно соединённых блоков. Надёжность каждого блока равна 0,7. Найдите надежность всего прибора.
Обозначим: событие А – прибор работает, событие Аi – работает i -ый блок.
Так как блоки соединены последовательно, то выход из строя каждого блока влечет за собой отказ прибора. Следовательно, надежность прибора, т.е. вероятность его безотказной работы, равна вероятности безотказной работы всех 5-ти блоков:
Р (А) = Р (А 1 А 2 А 3 А 4 А 5)
Вероятность совместного появления 5-ти независимых событий по теореме умножения вероятностей равна:
Р (А 1 А 2 А 3 А 4 А 5) = Р (А 1)· Р (А 2)· Р (А 3)· Р (А 4)· Р (А 5) = 0,75 = 0,168
Таким образом Р (А) = 0,168
3.18. Партия транзисторов, среди которых 10% брака, поступила на проверку.
Схема проверки такова, что с вероятностью 0.95 обнаруживается дефект, а с вероятностью 0,03 исправный транзистор может быть признан бракованным. Какова вероятность того, что случайным образом выбранный из партии транзистор будет признанбракованным?
Событие А – случайным образом выбранный транзистор будет признан бракованным.
По поводу исправности транзистора можно выдвинуть 2 гипотезы:
Н 1 – транзистор был неисправным;
Н 2 – транзистор был исправным.
Так как в партии транзисторов 10% брака, то вероятности этих гипотез составляют:
|
|
|
Р (Н 1) = 0,1 и Р (Н 2) = 0,9
Контроль: 0,1 + 0,9 = 1
По условию задачи условные вероятности признания транзистора неисправным составляют:

Тогда вероятность наступления события А – случайным образом выбранный транзис-тор будет признан бракованным – вычисляется по формуле полной вероятности:

На станциях отправления поездов находится 1000 автоматов для продажи билетов. Вероятность выхода из строя одного автомата в течение часа равна 0,004. Какова вероятность того, что в течение часа из строя выйдут 2 автомата?
По локальной теореме Лапласа вероятность того, что в п независимых испытаниях, в каждом из которых вероятность появления события равна р, событие наступит ровно k раз (безразлично, в какой последовательности), приближенно равна:

Здесь: n = 1000, k = 2, р = 0,004, q = 1–0,004 = 0,996
Вычисляем величину х и по таблице находим значение функции φ (х).

Так как функция φ (х) – четная, то φ (-1) = φ (1) = 0,2420
Искомая вероятность:

В партии из 20 телевизоров, шесть - с дефектом. Купили 2 телевизора. Написать закон распределения исправных телевизоров среди купленных. Построить многоугольник распределения.
Случайная величина Х – число исправных телевизоров среди 2 купленных – может принимать значения 0, 1 и 2. Вычислим соответствующие им вероятности.
Число N всевозможных исходов – выбор 2 изделий из 20 – это число сочетаний из 20 по 2:

1) Х =0. Выбрать 2 телевизора из 6-ти неисправных можно  способами. Тогда:
способами. Тогда: 
2) Х =1. Выбрать 1 исправный телевизор из 20–6=14 можно 14 способами; выбрать 1 неисправный телевизор из 6-ти можно 6 способами. Тогда:

3) Х =2. Выбрать 2 исправных телевизора из 14 можно  способами. Тогда:
способами. Тогда:

Контроль: 0,08+0,44+0,48 = 1
Закон распределения случайной величины X – числа исправных телевизоров среди 2 купленных:
| Х | |||
| рi | 0,08 | 0,44 | 0,48 |
Многоугольник распределения строим, откладывая по оси абсцисс возможные значе-ния случайной величины Х, а по оси ординат – соответствующие им вероятности.
|
|
|
На миллиметровке
Случайная величина X задана плотностью распределения

Найдите параметр С и математическое ожидание.
Параметр С находим из свойства плотности распределения:


Применяем метод интегрирования по частям:


При вычислении предела применяли правило Лопиталя.
Таким образом, плотность распределения случайной величины Х имеет вид:

Математическое ожидание вычисляется по формуле:

Так как все возможные значения Х принадлежат интервалу (1; ∞), то

Применяем метод интегрирования по частям:


7.18. Найти линейную среднюю квадратическую регрессию случайной величины Y на случайную величину X на основе заданного закона распределения двумерной случайной величины.
 Х
Y Х
Y
| |||
| 0,11 | 0,13 | 0,26 | |
| 0,21 | 0,06 | 0,23 |
Линейная средняя квадратическая регрессия Y на X имеет вид:
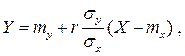
где mx=M (X) – математическое ожидание Х, my=M (Y) – математическое ожидание Y,  – среднее квадратическое отклонение X,
– среднее квадратическое отклонение X,  – среднее квадрати-ческое отклонение Y, r = µxy / (σ x σ y) – коэффициент корреляции величин X и Y,
– среднее квадрати-ческое отклонение Y, r = µxy / (σ x σ y) – коэффициент корреляции величин X и Y,
µxy – корреляционный момент.
Суммируя вероятности по столбцам, получаем закон распределения случайной величины Х:
| X | |||
| p | 0,32 | 0,19 | 0,49 |
Контроль: 0,32+0,19+0,49 = 1
Вычисляем числовые характеристики случайной величины Х:
Математическое ожидание М (Х) =  = 5·0,32 + 8·0,19 + 10·0,49 = 8,02
= 5·0,32 + 8·0,19 + 10·0,49 = 8,02
Дисперсия D (X) =  = 52·0,32 + 82·0,19 + 102·0,49 – 8,022 = 4,84
= 52·0,32 + 82·0,19 + 102·0,49 – 8,022 = 4,84
Среднее квадратическое отклонение 
Суммируя вероятности по строкам, получаем закон распределения случайной величины Y:
| Y | ||
| р | 0,5 | 0,5 |
Контроль: 0,5+0,5 = 1
Вычисляем числовые характеристики случайной величины Y:
Математическое ожидание М (Y) =  = 2·0,5 + 6·0,5 = 4
= 2·0,5 + 6·0,5 = 4
Дисперсия D (Y) =  = 22·0,5 + 62·0,5 – 42 = 4
= 22·0,5 + 62·0,5 – 42 = 4
Среднее квадратическое отклонение 
Вычислим математическое ожидание произведения случайных величин Х и Y:
М (XY) =  2·(5·0,11 + 8·0,13 + 10·0,26) + 6·(5·0,21 + 8·0,06 + 10·0,23) = 31,36
2·(5·0,11 + 8·0,13 + 10·0,26) + 6·(5·0,21 + 8·0,06 + 10·0,23) = 31,36
Корреляционный момент: µxy = М (XY) – М (Х)· М (Y) = 31,36 – 8,02·4 = – 0,72
Коэффициент корреляции: 
Линейная средняя квадратическая регрессия Y на X:
Y = 4 – 0,16·(X – 8,02) = 5,28 – 0,16 X
|
|
|


