 |
Определение коэффициента местных сопротивлений при различных режимах движения жидкости.
|
|
|
|
Теоретическая часть
Уравнение Бернулли для потока реальной жидкости.
Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:
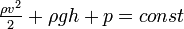
Здесь
 — плотность жидкости,
— плотность жидкости,
 — скорость потока,
— скорость потока,
 — высота, на которой находится рассматриваемый элемент жидкости,
— высота, на которой находится рассматриваемый элемент жидкости,
 — давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,
— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,
 — ускорение свободного падения.
— ускорение свободного падения.
Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Закон Бернулли справедлив и для ламинарных потоков газа. Явление понижения давления при увеличении скорости потока лежит в основе работы различного рода расходомеров (например труба Вентури), водо- и пароструйных насосов.
Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю, то есть таких жидкостей, которые не прилипают к поверхности трубы. На самом деле экспериментально установлено, что скорость жидкости на поверхности твердого тела почти всегда в точности равна нулю (кроме случаев отрыва струй при некоторых редких условиях).
Геометрический и энергетический смысл уравнения Бернулли для струйки идеальной жидкости.
Предположим, что центры тяжести живых сечений струйки 1–1 и 2–2 (рис 1) расположены на высотах z1 и z2 от плоскости сравнения 0–0 и что в этих центрах тяжести расположены пьезометрические трубки. Жидкость в каждой трубке поднимется на высоту hi =pi/сg, т.е. на пьезометрическую высоту. В уравнении (8) z1 и z2 (м) представляют собой геометрические высоты центров тяжести соответствующих живых сечений струйки над плоскостью сравнения, члены p1/сg и p2/сg (м) – пьезометрические высоты, отвечающие давлениям в указанных центрах тяжести. Третий член уравнения ui2/2g (м) является скоростным или динамическим напором, соответствующий скорости ui.
|
|
|
Отложим от точки А отрезок Аа, равный пьезометрической высоте p1/сg, а от точки В – отрезок Вb, равный p2/сg. Затем от точек a и b отложим отрезки аа/ и bb/, соответствующие скоростным напорам u12/2g и u22/2g.
Аналогичные построения можно сделать для ряда живых сечений, взятых вдоль элементарной струйки. Т.к. сумма трех членов ui2/2g, pi/сg и zi для идеальной жидкости постоянна вдоль оси струйки, то вершины вертикальных отрезков аа/ и bb/ располагаются на одинаковых вертикальных расстояниях от плоскости сравнения 0–0, и вершины этих отрезков должны лежать в одной горизонтальной плоскости, называемой напорной плоскостью 0/–0/. В случае идеальной жидкости напорная плоскость является горизонтальной. Если плавно соединить уровни жидкости в пьезометрических трубках, то получим пьезометрическую линию p–p.
Сумма трех высот называется полным гидродинамическим напором и обозначается HД. Следовательно, полный напор представляет собой сумму потенциального H = z + p/сg и скоростного hck= u2/2g напоров, т.е.
HД=H+hск.
Определение коэффициента местных сопротивлений при различных режимах движения жидкости.
Потери энергии (уменьшение гидравлического напора) можно наблюдать в движущейся жидкости не только на сравнительно длинных участках, но и на коротких. В одних случаях потери напора распределяются (иногда равномерно) по длине трубопровода - это линейные потери; в других - они сосредоточены на очень коротких участках, длиной которых можно пренебречь, - на так называемых местных гидравлических сопротивлениях: вентили, всевозможные закругления, сужения, расширения и т.д., короче всюду, где поток претерпевает деформацию. Источником потерь во всех случаях является вязкость жидкости.
|
|
|
Следует заметить, что потери напора и по длине и в местных гидравлических сопротивлениях существенным образом зависят от так называемого режима движения жидкости.
4.1. Режимы движения жидкости
При наблюдении за движением жидкости в трубах и каналах, можно заметить, что в одном случае жидкость сохраняет определенный строй своих частиц, а в других - перемещаются бессистемно. Однако исчерпывающие опыты по этому вопросу были проведены Рейнольдсом в 1883 г. На рис. 4.1 изображена установка, аналогичная той, на которой Рейнольдс производил свои опыты.

Рис. 4.1. Схема установки Рейнольдса
Установка состоит из резервуара А с водой, от которого отходит стеклянная труба В с краном С на конце, и сосуда D с водным раствором краски, которая может по трубке вводиться тонкой струйкой внутрь стеклянной трубы В.
Первый случай движения жидкости. Если немного приоткрыть кран С и дать возможность воде протекать в трубе с небольшой скоростью, а затем с помощью крана Е впустить краску в поток воды, то увидим, что введенная в трубу краска не будет перемешиваться с потоком воды. Струйка краски будет отчетливо видимой вдоль всей стеклянной трубы, что указывает на слоистый характер течения жидкости и на отсутствие перемешивания. Если при этом, если к трубе подсоединить пьезометр или трубку Пито, то они покажут неизменность давления и скорости по времени. Такой режим движения называется ламинарный.
Второй случай движения жидкости. При постепенном увеличении скорости течения воды в трубе путем открытия крана С картина течения вначале не меняется, но затем при определенной скорости течения наступает быстрое ее изменение. Струйка краски по выходе из трубки начинает колебаться, затем размывается и перемешивается с потоком воды, причем становятся заметными вихреобразования и вращательное движение жидкости. Пьезометр и трубка Пито при этом покажут непрерывные пульсации давления и скорости в потоке воды. Такое течение называется турбулентным (рис.4.1, вверху).
Если уменьшить скорость потока, то восстановится ламинарное течение.
|
|
|
Итак, ламинарным называется слоистое течение без перемешивания частиц жидкости и без пульсации скорости и давления. При ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, при этом отсутствуют поперечные перемещения частиц жидкости.
Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости с пульсациями скоростей и давлений. Наряду с основным продольным перемещением жидкости наблюдаются поперечные перемещения и вращательные движения отдельных объемов жидкости. Переход от ламинарного режима к турбулентному наблюдается при определенной скорости движения жидкости. Эта скорость называется критической υ кр.
Значение этой скорости прямо пропорционально кинематической вязкости жидкости и обратно пропорционально диаметру трубы.
где ν - кинематическая вязкость;
k - безразмерный коэффициент;
d - внутренний диаметр трубы.
Входящий в эту формулу безразмерный коэффициент k, одинаков для всех жидкостей и газов, а также для любых диаметров труб. Этот коэффициент называется критическим числом Рейнольдса Reкр и определяется следующим образом:
Как показывает опыт, для труб круглого сечения Reкр примерно равно 2300.
Таким образом, критерий подобия Рейнольдса позволяет судить о режиме течения жидкости в трубе. При Re < Reкр течение является ламинарным, а при Re > Reкр течение является турбулентным. Точнее говоря, вполне развитое турбулентное течение в трубах устанавливается лишь при Re примерно равно 4000, а при Re = 2300…4000 имеет место переходная, критическая область.
Режим движения жидкости напрямую влияет на степень гидравлического сопротивления трубопроводов.
4.2. Кавитация
В некоторых случаях при движении жидкости в закрытых руслах происходит явление, связанное с изменением агрегатного состояния жидкости, т.е. превращение ее в пар с выделением из жидкости растворенных в ней газов.
Наглядно это явление можно продемонстрировать на простом устройстве, состоящим из трубы, на отдельном участке которой установлена прозрачная трубка Вентури (рис.4.2). Вода под давлением движется от сечения 1-1 через сечение 2-2 к сечению 3-3. Как видно из рисунка, сечение 2-2 имеет меньший диаметр. Скорость течения жидкости в трубе можно изменять, например, установленным после сечения 3-3 краном.
|
|
|

Рис. 4.2. Схема трубки для демонстрации кавитации
При небольшой скорости никаких видимых изменений в движении жидкости не происходит. При увеличении скорости движения жидкости в узком сечении трубки Вентури 2-2 появляется отчетливая зона с образованием пузырьков газа. Образуется область местного кипения, т.е. образование пара с выделением растворенного в воде газа. Далее при подходе жидкости к сечению 3-3 это явление исчезает.
Это явление обусловлено следующим. Известно, что при движении жидкой или газообразной среды, давление в ней падает. Причем, чем выше скорость движения среды, тем давление в ней ниже. Поэтому, при течении жидкости через местное сужение 2-2, согласно уравнению неразрывности течений, увеличивается скорость с одновременным падением давления в этом месте. Если абсолютное давление при этом достигает значения равного давлению насыщенных паров жидкости при данной температуре или значения равного давлению, при котором начинается выделение из нее растворимых газов, то в данном месте потока наблюдается интенсивное парообразование (кипение) и выделение газов. Такое явление называется кавитацией.
При дальнейшем движении жидкости к сечению 3-3, пузырьки исчезают, т.е. происходит резкое уменьшение их размеров. В то время, когда пузырек исчезает (схлопывается), в точке его схлопывания происходит резкое увеличение давления, которое передается на соседние объемы жидкости и через них на стенки трубопровода. Таким образом, от таких многочисленных местных повышений давлений (гидроударов), возникает вибрация.
Таким образом, кавитация - это местное нарушение сплошности течения с образованием паровых и газовых пузырей (каверн), обусловленное местным падением давления в потоке.
Кавитация в обычных случаях является нежелательным явлением, и ее не следует допускать в трубопроводах и других элементах гидросистем. Кавитация возникает в кранах, вентилях, задвижках, жиклерах и т.д.
Кавитация может иметь место в гидромашинах (насосах и гидротурбинах), снижая при этом их коэффициент полезного действия, а при длительном воздействии кавитации происходит разрушение деталей, подверженных вибрации. Кроме этого разрушаются стенки трубопроводов, уменьшается их пропускная способность вследствие уменьшения живого сечения трубы.
|
|
|
4.3. Потери напора при ламинарном течении жидкости
Как показывают исследования, при ламинарном течении жидкости в круглой трубе максимальная скорость находится на оси трубы. У стенок трубы скорость равна нулю, т.к. частицы жидкости покрывают внутреннюю поверхность трубопровода тонким неподвижным слоем. От стенок трубы к ее оси скорости нарастаю плавно. График распределения скоростей по поперечному сечению потока представляет собой параболоид вращения, а сечение параболоида осевой плоскостью - квадратичную параболу (рис.4.3).
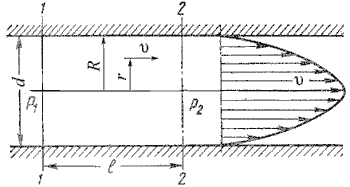
Рис. 4.3. Схема для рассмотрения ламинарного потока
Уравнение, связывающее переменные υ и r, имеет следующий вид:
где P1 и P2 - давления соответственно в сечениях 1 и 2.
У стенок трубы величина r = R,, значит скорость υ = 0, а при r = 0 (на оси потока) скорость будет максимальной
Теперь определим расход жидкости при ламинарном течении в круглой трубе. Так как эпюра распределения скоростей в круглой трубе имеет вид параболоида вращения с максимальным значением скорости в центре трубы, то расход жидкости численно равен объему этого параболоида. Определим этот объем.
Максимальная скорость дает высоту параболоида
Как известно из геометрии, объем параболоида высотой h и площадью ρR2 равена в нашем случае
Если вместо R подставить диаметр трубы d, то формула (4.4) приобретет вид
Расход в трубе можно выразить через среднюю скорость:откуда
Для определения потерь напора при ламинарном течении жидкости в круглой трубе рассмотрим участок трубы длиной l, по которому поток течет в условиях ламинарного режима (рис.4.3).
Если в формуле динамический коэффициент вязкости μ заменить через кинематический коэффициент вязкости υ и плотность ρ (μ = υ ρ) и разделить обе части равенства на объемный вес жидкости γ = ρ g, то получим:
Так как левая часть полученного равенства равна потерям напора hпот в трубе постоянного диаметра, то окончательно это равенство примет вид:
Уравнение может быть преобразовано в универсальную формулу Вейсбаха-Дарси, которая окончательно записывается так:
где λ - коэффициент гидравлического трения, который для ламинарного потока вычисляется по выражению:
Однако при ламинарном режиме для определения коэффициента гидравлического трения λ Т.М. Башта рекомендует при Re < 2300 применять формулу
4.4. Потери напора при турбулентном течении жидкости
Как было указано в п.4.1, для турбулентного течения характерно перемешивание жидкости, пульсации скоростей и давлений. Если с помощью особо чувствительного прибора-самописца измерять пульсации, например, скорости по времени в фиксированной точке потока, то получим картину, подобную показанной на рис.4.4. Скорость беспорядочно колеблется около некоторого осредненного по времени значения υ оср, которое данном случае остается постоянным.
Характер линий тока в трубе в данный момент времени отличается большим разнообразием (рис.4.5).


Рис. 4.4. Пульсация скорости в турбулентном потоке. Рис. 4.5. Характер линий тока в турбулентном потоке
При турбулентном режиме движения жидкости в трубах эпюра распределения скоростей имеет вид, показанный на рис. 4.6. В тонком пристенном слое толщиной δ жидкость течет в ламинарном режиме, а остальные слои текут в турбулентном режиме, и называются турбулентным ядром. Таким образом, строго говоря, турбулентного движения в чистом виде не существует. Оно сопровождается ламинарным движением у стенок, хотя слой δ с ламинарным режимом весьма мал по сравнению с турбулентным ядром.

Рис. 4.6. Модель турбулентного режима движения жидкости
Основной расчетной формулой для потерь напора при турбулентном течении жидкости в круглых трубах является уже приводившаяся выше эмпирическая формула, называемая формулой Вейсбаха-Дарси и имеющая следующий вид:
Различие заключается лишь в значениях коэффициента гидравлического трения λ. Этот коэффициент зависит от числа Рейнольдса Re и от безразмерного геометрического фактора - относительной шероховатости Δ/d (или Δ/r0, где r0 - радиус трубы).
Впервые наиболее исчерпывающей работы по определению были даны И.И. Никурадзе, который на основе опытных данных построил график зависимости lg(1000λ) от lg Re для ряда значений Δ/r 0. Опыты Никурадзе были проведены на трубах с искусственно заданной шероховатостью, полученной путем приклейки песчинок определенного размера на внутренние стенки трубопровода. Результаты этих исследований представлены на рис. 4.7, где построены кривые зависимости lg (1000λ) от lg Re для ряда значений Δ/r0.
Прямая I соответствует ламинарному режиму движения жидкости.
Далее на графике можно рассматривать три области.
Первая область - область малых Re и Δ/r0, где коэффициент λ не зависит от шероховатости, а определяется лишь числом Re (отмечена на рис.4.7 прямой II). Это область гидравлически гладких труб. Если число Рейнольдса лежит в диапазоне 4000 < Re < 10(d / Δ э) коэффициент λ определяется по полуэмпирической формуле Блазиуса
Для определения существует также эмпирическая формула П.К. Конакова, которая применима для гидравлически гладких труб
Рис. 4.7. График Никурадзе
Во второй области, расположенной между линий II и пунктирной линией справа, коэффициент λ зависит одновременно от двух параметров - числа Re и относительной шероховатости Δ/r0, которую можно заменить на Δэ. Для определения коэффициента λ в этой области может служить универсальная формула А.Д. Альтшуля:
где Δэ - эквивалентная абсолютная шероховатость.
Характерные значения Δэ (в мм) для труб из различных материалов приведены ниже: Стекло 0
Трубы, тянутые из латуни, свинца, меди 0…0,002
Высококачественные бесшовные стальные трубы 0,06…0,2
Стальные трубы 0,1…0,5
Чугунные асфальтированные трубы 0,1…0,2
Чугунные трубы 0,2…1,0
Третья область - область больших Re и Δ/r0, где коэффициент λ не зависит от числа Re, а определяется лишь относительной шероховатостью (область расположена справа от пунктирной линии). Это область шероховатых труб, в которой все линии с различными шероховатостями параллельны между собой. Эту область называют областью автомодельности или режимом квадратичного сопротивления, т.к. здесь гидравлические потери пропорциональны квадрату скорости.
Определение λ для этой области производят по упрощенной формуле Альтшуля:

или по формуле Прандтля - Никурадзе:
Итак, потери напора, определяемые по формуле Вейсбаха-Дарси, можно определить, зная коэффициент гидравлического сопротивления, который определяется в зависимости от числа Рейнольдса Re и от эквивалентной абсолютной шероховатости Δэ. Для удобства сводные данные по определению λ представлены в таблице 4.1.
Пользоваться приведенными в табл. 4.1 формулами для определения коэффициента λ не всегда удобно. Для облегчения расчетов можно воспользоваться номограммой Колбрука-Уайта (рис.4.8), при помощи которой по известным Re и Δэ/ d весьма просто определяется λ.
Таблица 4.1
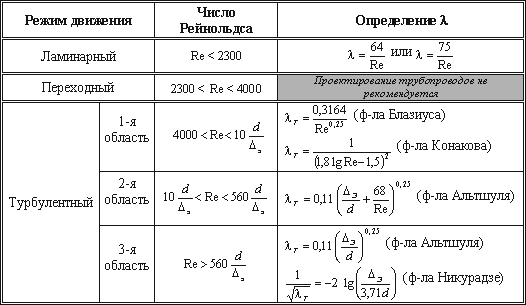

Таблица для определения коэффициента гидравлического трения
Рис. 4.8. Номограмма Колбрука-Уайта для определения коэффициента гидравлического трения
4.5. Местные гидравлические сопротивления
Все гидравлические потери энергии делятся на два типа: потери на трение по длине трубопроводов (рассмотрены в п.4.3 и 4.4) и местные потери, вызванные такими элементами трубопроводов, в которых вследствие изменения размеров или конфигурации русла происходит изменение скорости потока, отрыв потока от стенок русла и возникновение вихреобразования.
Простейшие местные гидравлические сопротивления можно разделить на расширения, сужения и повороты русла, каждое из которых может быть внезапным или постепенным. Более сложные случаи местного сопротивления представляют собой соединения или комбинации перечисленных простейших сопротивлений.
Рассмотрим простейшие местные сопротивления при турбулентном режиме течения в трубе.
1. Внезапное расширение русла. Потеря напора (энергии) при внезапном расширении русла расходуется на вихреобразование, связанное с отрывом потока от стенок, т.е. на поддержание вращательного непрерывного движения жидких масс с постоянным их обновлением.

Рис. 4.9. Внезапное расширение трубы
При внезапном расширении русла (трубы) (рис.4.9) поток срывается с угла и расширяется не внезапно, как русло, а постепенно, причем в кольцевом пространстве между потоком и стенкой трубы образуются вихри, которые и являются причиной потерь энергии. Рассмотрим два сечения потока: 1-1 - в плоскости расширения трубы и 2-2 - в том месте, где поток, расширившись, заполнил все сечение широкой трубы. Так как поток между рассматриваемыми сечениями расширяется, то скорость его уменьшается, а давление возрастает. Поэтому второй пьезометр показывает высоту на ΔH большую, чем первый; но если бы потерь напора в данном месте не было, то второй пьезометр показал бы высоту большую еще на hрасш. Эта высота и есть местная потеря напора на расширение, которая определяется по формуле:
где S1, S2 - площадь поперечных сечений 1-1 и 2-2.
Это выражение является следствием теоремы Борда, которая гласит, что потеря напора при внезапном расширении русла равна скоростному напору, определенному по разности скоростей
Выражение (1 - S1/S2)2 обозначается греческой буквой ζ (дзета) и называется коэффициентом потерь, таким образом
2. Постепенное расширение русла. Постепенно расширяющаяся труба называется диффузором (рис.4.10). Течение скорости в диффузоре сопровождается ее уменьшением и увеличением давления, а следовательно, преобразованием кинетической энергии жидкости в энергию давления. В диффузоре, так же как и при внезапном расширении русла, происходит отрыв основного потока от стенки и вихреобразования. Интенсивность этих явлений возрастает с увеличением угла расширения диффузора α.

Рис. 4.10. Постепенное расширение трубы
Кроме того, в диффузоре имеются и обычные потери на терние, подобные тем, которые возникают в трубах постоянного сечения. Полную потерю напора в диффузоре рассматривают как сумму двух слагаемых:
где hтр и hрасш - потери напора на трение и расширение (вихреобразование).
где n = S2/S1 = (r2/r1) 2 - степень расширения диффузора. Потеря напора на расширение hрасш имеет ту же самую природу, что и при внезапном расширении русла
где k - коэффициент смягчения, при α= 5…20°, k = sinα.
Учитывая это полную потерю напора можно переписать в виде:
откуда коэффициент сопротивления диффузора можно выразить формулой

Рис. 4.11. Зависимость ζдиф от угла
Функция ζ = f(α)имеет минимум при некотором наивыгоднейшем оптимальном значении угла α, оптимальное значение которого определится следующим выражением:
При подстановке в эту формулу λТ =0,015…0,025 и n = 2…4 получим αопт = 6 (рис.4.11).
3. Внезапное сужение русла. В этом случае потеря напора обусловлена трением потока при входе в более узкую трубу и потерями на вихреобразование, которые образуются в кольцевом пространстве вокруг суженой части потока (рис.4.12).

Рис. 4.12. Внезапное сужение трубы 4.13. Конфузор
Полная потеря напора определится по формуле;
где коэффициент сопротивления сужения определяется по полуэмпирической формуле И.Е. Идельчика:
в которой n = S1/S2 - степень сужения.
При выходе трубы из резервуара больших размеров, когда можно считать, что S2/S1 = 0, а также при отсутствии закругления входного угла, коэффициент сопротивления ζсуж = 0,5.
4. Постепенное сужение русла. Данное местное сопротивление представляет собой коническую сходящуюся трубу, которая называется конфузором (рис.4.13). Течение жидкости в конфузоре сопровождается увеличением скорости и падением давления. В конфузоре имеются лишь потери на трение
где коэффициент сопротивления конфузора определяется по формуле
в которой n = S1/S2 - степень сужения.
Небольшое вихреобразование и отрыв потока от стенки с одновременным сжатием потока возникает лишь на выходе из конфузора в месте соединения конической трубы с цилиндрической. Закруглением входного угла можно значительно уменьшить потерю напора при входе в трубу. Конфузор с плавно сопряженными цилиндрическими и коническими частями называется соплом (рис.4.14).

Рис. 4.14. Сопло
5. Внезапный поворот трубы (колено). Данный вид местного сопротивления (рис.4.15) вызывает значительные потери энергии, т.к. в нем происходят отрыв потока и вихреобразования, причем потери тем больше, чем больше угол δ. Потерю напора рассчитывают по формуле
где ζкол - коэффициент сопротивления колена круглого сечения, который определяется по графику в зависимости от угла колена δ (рис.4.16).

Рис. 4.15. Рис. 4.16. Зависимости ζкол от угла δ Рис. 4.17. Отвод
6. Постепенный поворот трубы (закругленное колено или отвод). Плавность поворота значительно уменьшает интенсивность вихреобразования, а следовательно, и сопротивление отвода по сравнению с коленом. Это уменьшение тем больше, чем больше относительный радиус кривизны отвода R / d рис.4.17). Коэффициент сопротивления отвода ζотв зависит от отношения R / d, угла δ, а также формы поперечного сечения трубы.
Для отводов круглого сечения с углом δ= 90 и R/d 1 при турбулентном течении можно воспользоваться эмпирической формулой:
Для углов δ 70° коэффициент сопротивления, а при δ 100°
Потеря напора в колене определится как
Все выше изложенное относится к турбулентному движению жидкости. При ламинарном движении местные сопротивления играют малую роль при определении общего сопротивления трубопровода. Кроме этого закон сопротивления при ламинарном режиме является более сложным и исследован в меньшей степени.
|
|
|


