Ontological status of basic concepts of mathematical conception of N. Burbaky

Аннотация

 

При анализе методологического подхода к математике группы Н. Бурбаки раскрыт онтологический статус понятий «основные структуры» и «математические топологии».

Ключевые слова: математическая онтология, основные структуры, математические топологии.

Annotation

Ontological status of basic concepts of mathematical conception of N. Burbaky

At the analysis of methodological approach by mathematics of group of N. Burbaky ontological status of concepts is exposed «basic structures» and «mathematical to the topology».

Keywords: mathematical ontology, basic structures mathematical to the topology.

 

 

Вопрос об отношении математических объектов и целостных структур реального мира - основной в объяснения природы математики как строгой науки. Лишь в ходе решения проблемы о статусе математических понятий и теорий, становится возможным рассматривать прочие философские проблемы математики, трактовка которых непосредственно зависит от того, истолковываются ли математические понятия как отражения свойств объектов реального мира, либо же они трактуются как «идеи», имеющие «самостоятельное» существование, являющиеся продуктом творчества трансцендентального субъекта.

В рамках античной парадигмы математической онтологии причиной различий в трактовке Платоном и Аристотелем онтологического статуса математических сущностей является разница между объективным идеализмом Платона, как идеалистическим плюрализмом, и объективным идеализмом Аристотеля, как идеалистическим монизмом. По убеждению Платона, математика, как абстрактное построение разума, оказывается моделью, порождающей, при её приложении к познанию первоначал всего сущего, остальные виды знания. Она в то же время и модель, порождённая остальными видами знания. По Аристотелю, математическое познание - это познание формы единого предмета, присоединение к которой нового элемента знания позволяет рассматривать образовавшийся элемент как субстанцию. Форма - общее, реально же единичное.

В истории философской и математической мысли взгляды Платона и Аристотеля неоднократно подвергались переосмыслению. Вопросы о том, что в философском контексте представляют собой математические предметы и объекты, до настоящего времени не имеет однозначного решения.

Автор при анализе методологического подхода к математике семинара Н. Бурбаки ставит целью раскрыть онтологический статус основных понятий их математической концепции - «основные структуры» и «математические топологии». Необходимо отметить, что учение французских математиков с философской точки зрения не анализировалось.

Н. Бурбаки - собирательный псевдоним, под которым группа математиков во Франции с 1939г. выступает с попыткой осуществить идею, исходящую от Д. Гильберта - рассмотреть различные математические теории с позиций формального аксиоматического метода. В многотомном трактате семинара Н. Бурбаки «Элементы математики», выходящем с 1939 г., развивается формальная аксиоматическая система, которая, по замыслу авторов, должна охватить главнейшие разделы математики как «частные аспекты общей концепции». Изложение носит абстрактный и формализованный характер, дается лишь логический каркас теорий. Основы изложения составляют структуры, определяемые посредством аксиом, например структуры порядка, группы, топологические структуры. Способ рассуждения - от общего к частному. Классификация разделов математики производится по типам структур. Она значительно отличается от традиционной классификации.

Структурный подход к математике Н. Бурбаки, если рассматривать его с позиции онтологического статуса её объектов, обладает двумя важными особенностями. Во-первых, проекцией некоторых установок целостных структур реального мира. Во-вторых, универсальными принципами математических операций. Необходимость последних появляется вследствие использования алгоритмов. Система безусловных предписаний охватывает все возможные условия существования абстрактных сущностей вне зависимости от их смысла.

Введение удобного и сжатого языка алгоритмов всегда сопровождается рассуждениями, принадлежащими к метаматематике. Д. Гильберт, а затем и группа Н. Бурбаки показали, что эта дисциплина, абстрагируясь от всякого значения, которое могло бы первоначально приписываться словам или фразам формализованных математических текстов, рассматривает их как структуры заранее данных объектов, в которых важен лишь порядок расположения этих объектов. В «Общей топологии» встречаются примеры с использованием ресурсов арифметики. Это касается, в частности, факторпространства, когда рассматриваются произведения факторпространств. В метаматематических рассуждениях в отношении факторпространств описываются операции, поддающиеся выполнению и контролю. Сами метаматематические рассуждения записаны с использованием «дедуктивных критериев».

По убеждению группы французских математиков, формализованная математика не может быть записана вся полностью, «… потому приходится питать доверие к тому, что можно назвать здравым смыслом математика, - доверие, аналогичное тому, которое бухгалтер и инженер, не подозревая о существовании аксиом Пеано, питают к формуле или численной таблице и которое, в конечном счете, основано на том, что оно никогда не было подорвано фактами» [1. с. 272]. Математикам приходится покидать формализованную математику. Все математические тексты пишутся отчасти обычным языком, отчасти с помощью формул, составляющих частичные формализации, специальные и неполные, из которых алгебраическое исчисление служит наиболее известным примером. Логика, подчиненная аксиомам собственно математики, «… не определяет ни того, что такое математика, ни того, чем занимаются математики» [1. с. 256], а представляет собой «…не больше и не меньше, как грамматику языка, которым мы пользуемся, языка, который должен был существовать еще до того, как могла быть построена грамматика» [1. с. 256]. Ситуация с бесконечными множествами продемонстрировала необходимость новых модификаций логики при развитии математики.

Автор особо стремится подчеркнуть то обстоятельство, что, применяя аксиому выбора и закон исключающего третьего, Н. Бурбаки отвергается концепция Д. Гильберта о непротиворечивости в отношении существования математических объектов. По поводу непротиворечивости своих построений они отмечали, что все противоречия возможно преодолеть способом, «… позволяющим избежать всех возражений и не оставляющим сомнения в правильности рассуждений» [1. с. 256]. В отношении непротиворечивости группой Н. Бурбаки делается утверждение: «…как показывает анализ исторического развития математики, было бы неверно утверждать, что математика свободна от противоречий; непротиворечивость предстаёт как цель, к которой следует стремиться, как некое данное Богом качество, ниспосланное нам раз и навсегда. С древнейших времен критические пересмотры оснований всей математики в целом или любого из ее разделов почти неизменно сменялись периодами неуверенности, когда возникали противоречия, которые приходилось решать... Но вот уже 25 веков математики имеют обыкновение исправлять свои ошибки и видеть в этом обогащение, а не обеднение своей науки; это дает им право смотреть в будущее спокойно» [1. с. 259].

Выражая полную уверенность в том, что любые возникающие проблемы математики непременно будут разрешены, Н. Бурбаки высказывается мнение о том, что «… если когда-нибудь будет доказано, что математика противоречива, то, скорее всего, станет определённо ясно, какому правилу следует приписать полученный результат. Отбросив это правило, или надлежащим образом видоизменив его, мы избавимся от противоречия. Иначе говоря, математика изменит направление своего развития, но не перестанет быть наукой. Сказанное не просто умозаключение: нечто подобное произошло после открытия иррациональных чисел. Мы далеки от мысли оплакивать это открытие, потому что оно вскрыло противоречие в пифагорейской математике, а, напротив, сегодня мы считаем его одной из великих побед человеческого духа» [1. с. 265]. В качестве основных методов разрешения математических противоречий Н. Бурбаки на первый план были выведены: во-первых, анализ математических структур; во-вторых, большое внимание было уделено взаимопроникновению алгебры, арифметики и теории функций.

Автор отмечает, что непротиворечивость - это одна из проблем, занимающих современных логиков и математиков. Математическая теория называется противоречивой, если какая-либо теорема доказывается в ней вместе со своим отрицанием. В этом случае, исходя из правил умозаключения, лежащих в основе построения синтаксиса формализованных языков, можно сделать вывод о том, что любая теорема одновременно и истинна, и ложна в данной теории. Если приходим к противоречию, то не можем оставить его существовать, не обесценивая теории, в которой оно возникло.

Метаматематика может рассмотреть проблемы непротиворечивости своими собственными методами. Определить, что некоторая теория непротиворечива, - значит утверждать, что она содержит правильное формализованное доказательство, оканчивающееся заключением a = a. Чтобы избежать проблемы непротиворечивости, необходимо, чтобы непротиворечивость богатого формализованного языка можно было доказать посредством рассуждений, формализуемых в языке менее богатом и, тем самым, более достойном доверия. Но теорема К. Гёделя о неполноте утверждает, что это невозможно для языка, достаточно богатого аксиомами. При доказательствах относительной непротиворечивости, устанавливающих непротиворечивость одной теории в предположении непротиворечивости другой теории, например теории множеств, метаматематическая часть рассуждения достаточно проста. Современные математические теории, в том числе и теория математического структурализма Н. Бурбаки, привязываются, как правило, в отношении логической проверки непротиворечивости к теории множеств. Отсюда можно сделать вывод о том, что всякое противоречие, встреченное в одной из этих теорий, дало бы повод противоречию в самой теории множеств. Но это не аргумент, позволяющий судить о непротиворечивости самой теории множеств. Со времени достаточно точной формулировки аксиом теории множеств из них стали извлекать следствия в самых разнообразных областях математики.

Автор подчёркивает, что любое противоречие формализованной математической теории, в основании которой лежат принципы теории множеств (это касается и построений Н. Бурбаки), было бы внутренне присуще принципам, положенным в основание самой теории множеств, а потому необходимо было бы изменить эти принципы. Но в отношении всех формализованных математических теорий, основывающихся на принципах теории множеств, следует отметить, что они опираются на теорию, в которой установлены парадоксы. онтологический математический сущность бурбаки

В отношении вырабатываемых систем доказательств, следует подчеркнуть, что формалистская математика, начиная с Д. Гильберта (это относится и к структурному подходу Н. Бурбаки), выросшая как отрицание интуитивной позиции, возвела в культ форму, знак и правила оперирования со знаками. В определенном отношении это прогресс. Достижения структурного анализа Н. Бурбаки в математике никогда не будут перечеркнуты. Но этот подход утвердил вместе с тем целую систему ложных верований. Всякое содержательное мышление в современной математике стало рассматриваться как нуждающееся в логическом анализе.

Формализация стала пониматься как единственный способ окончательного утверждения какого-либо результата, причем достоверность была отождествлена с финитностью. Если в формальном подходе невозможно вывести какую-либо формулу, соответствующую утверждению о непротиворечивости математического объекта, то достоверного обоснования не существует. В действительности формализм и в частности структурализм вовсе не исключают содержательного рассуждения, обосновывающего непротиворечивость с предельной достоверностью, следует обратиться лишь к «Коммуникативной алгебре» Н. Бурбаки. Содержательное аподиктическое доказательство не нуждается в формализации для подтверждения своей надежности. Это значит, что содержательное обоснование математики вполне независимо и не ограничивается в своих возможностях теорией структур. Так, например, «Коммуникативная алгебра», в которой рассмотрены алгоритмы представления ряда функций в виде векторных пространств - локальных и глобальных колец, а также полей - это результат развития теории чисел и аналитической геометрии.

Автор ставит цель - выявить онтологический статус алгоритма - жёстко заданной последовательности непустого множества коммуникативных операций - кольца, осуществляемых в «Коммуникативной алгебре» Н. Бурбаки. Отметим, что в кольце осуществляются бинарные операции - операции с двумя объектами, обозначаемые знаком + и - и записью объектов друг возле друга. В коммуникативной алгебре присутствует также операция «равенство» и особый элемент 0. Все операции монотонны относительно равенства. Это значит, что если вычитаются или складываются объекты одной операции, то соответственно уменьшаются или увеличиваются объекты другой операции. Но, прежде всего, необходимо рассмотреть понятие алгоритма и его места в математике.

Следует особо оговорить, что построение любого алгоритма, как и системы доказательств, - это особые математические проблемы - неразрешимости. Несмотря на то, что понятие алгоритма является едва ли не самым распространенным в современной математике, природа этого понятия стала ясной только с появлением математической логики. С исторической точки зрения понятие алгоритма связано с алгеброй, потому что именно там оно появилось впервые. Интересно то обстоятельство, что слова алгебра и алгоритм обязаны своим возникновением одному человеку - узбекскому математику Аль Хорезми.

Математика имеет дело с математическими объектами, среди которых можно назвать числа, функции, множества, фигуры и т.д. Суть математики состоит в доказательстве истинных утверждений об этих объектах; и если есть такое доказательство, объект, фигурирующий в утверждении, считается существующим. Вопрос о том, где он существует: в мире идеальных сущностей, или же в уме у математика, или же во внешнем мире, и занимает философов математики. Важным фактом является то, что алгоритм в обычном его понимании не является традиционным математическим объектом.

Для понимания этого важного факта следует обратиться к тому, что представляют собой математические утверждения. Обычно они являются дескриптивными - описывающими свойства математических объектов. В более широком смысле можно полагать, что математические утверждения описывают математическую реальность, что бы под этим ни понималось.

Все алгоритмы носят императивный характер. Они представляют собой предписания. В этом смысле они не являются математическими объектами в их традиционном понимании. Императивы не есть часть математики. Это представляется странным, но следует учесть, что алгоритмы появляются в математических доказательствах в виде текста, который никак не подходит под определение математического объекта как чего-то такого, что описывается математическими утверждениями.

В «Коммуникативной алгебре» Н. Бурбаки все предписания представлены в виде диаграмм:

 

0 → F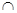^’  F^’’ - → F^’ /(F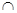^’  F^’’) → 0

↓↓ ↓

→ F^’’ - →F^’ + F^’’ - → (F^’ + F^’’) / F^’ → 0

 

которые затем снабжены дескриптивными высказываниями в виде лемм и теорем. Например, лемма представляющая эту диаграмму:

Пусть E - правый модуль A модуль, F - левый модуль A модуль и F^’, F^’’ такие подмодули в F, что F = F^’ + F^’’. Тогда пересечение канонических образов модулей E  F^’ и E  F^’’ в модуле E  F равно каноническому образу модуля E  (F^’  F^’’). [2. с.31].

Для понимания природы алгоритма и его определения в качестве математического объекта необходимо фиксировать различие между дескриптивными и императивными утверждениями - в данном случае между диаграммой, как жёстко установленной последовательностью действий, и леммой, как дескриптивным высказыванием. Это первое противопоставление, которое необходимо при обсуждении вопроса о статусе алгоритма. Другим противопоставлением является противопоставление классической и постклассической математики или, более точно, классического аксиоматического метода и современного аксиоматического метода. Крайне важным будет также разделение синтаксических и семантических аспектов математических построений.

Впервые объекты, которые можно сопоставить с алгоритмами, появились в классической алгебре. Именно там алгоритмы стали претендовать на то, чтобы их можно было уподобить математическим объектам. Рождение постклассической математики также связано с алгеброй, которая ввела в обиход совершенно новые математические объекты. Понятие алгоритма стало формализуемым и более понятным в рамках математической логики. Следует принять во внимание, что до возникновения математической логики алгебра в известной степени играла роль логики внутри математики. Обычная логика, связанная с именем Аристотеля, относилась к законам мышления и не играла какой-либо значимой роли в математике. Кодификация в современной постклассической математике, к которой относится и структурализм Н. Бурбаки, была осуществлена средствами математической логики, которую многие исследователи совсем не соотносят с законами мышления.

Объектом философского анализа стала модель императивного высказывания и представляющего его высказывания дескриптивного. Выявляя онтологический статус алгоритма - жёстко заданной последовательности непустого множества коммуникативных операций - кольца, осуществляемых в «Коммуникативной алгебре» Н. Бурбаки, автор делает следующий вывод. Объектом онтологического упорядочения могут оказаться алгоритмические построения, но только в том случае, если в них будут в достаточной степени оговорены составляющие операционной рационализации.

Не прибегая к анализу конкретного содержания алгоритмических построений, трудно оценить представление французских математиков об их собственной науке. Своеобразие математики, как системы описания хода и результатов познавательных процессов, делает большинство её построений недоступными для философского осмысления; это касается и такого объекта, как алгоритм. Философия не обладает методом анализа, а затем трансляции математических конструкций в свои собственные определения. Но отметим, что общие философские принципы предоставляют философу аппарат, позволяющий обсудить проблему контура, очерчивающего предмет математических методов. Исходя из этого, философ получает возможность установления некоторых немногих исходных посылок, на которых, если руководствоваться философским пониманием, построена математика.

Автор подчёркивает, что характерным отличием математического мышления группы Н. Бурбаки следует признать особенность понимания таких сущностей, как типы структур, рассматриваемых как классы отношений, но не классы объектов. Группе французских математиков свойственно отождествлять математическое знание с конструкцией, некой «теории как таковой», на основании данной посылки, определять структурный подход в качестве метатеории, которая позволяет анализировать методологические особенности самых разнообразных областей математического знания.

В отношении онтологического статуса основных понятий математической концепции Н. Бурбаки автор высказывает мнение, что математические объекты трактуются математическим семинаром как существующие в определённом смысле объективно. Математическая истина - это откровение, а не изобретение. Концепция группы французских математиков - это концепция математического реализма, которая смыкается с платонизмом. Она постулирует, что математические объекты являются абстрактными, вечными и причинно не связанными с материальными предметами и эмпирическим опытом.

Достижения структурного подхода Н. Бурбаки в математике никогда не будут перечеркнуты. Но этот подход утвердил систему ложных верований. Всякое содержательное мышление в современной математике стало рассматриваться как нуждающееся в логическом анализе. Формализация стала пониматься как единственный способ окончательного утверждения какого-либо результата, причем достоверность была отождествлена с финитностью.

 

Литературные источники:

1. Бурбаки Н. Очерки по истории математики / Н. Бурбаки. - М.: Мир, 1963. - 420с.

2. Бурбаки Н. Коммуникативная алгебра / Н. Бурбаки. - М.: Мир, 1971. - 707с.

Поделиться:

Воспользуйтесь поиском по сайту: