Матричные игры с природой (теория статистических решений)

Теория игр.

Основные понятия и определения

1. Матричные игры

Тео́рия игр – это математическаятеория конфликтных ситуаций, т.е. таких ситуаций, в которых сталкиваются интересы двух или более сторон, преследующих различные цели.

 

Конфликтные ситуации – это ситуации, в которых эффективность решения, принимаемого одной стороной (выигрыш), зависит от действий другой стороны.

 

Игра представляет собой математическую модель реальной конфликтной ситуации. От реальной конфликтной ситуации она отличается тем, что ведется по определенным правилам, в которых должны быть указаны:

- порядок чередования действий (ходов) участников;

- правила выполнения каждого хода;

- количественный результат игры (выигрыш, проигрыш), к которому приводит данная совокупность ходов.

Игра, в которой участвуют два игрока А и В, называется парной, если игроков больше двух, то это игра – множественная. Игра, в которой выигрыш одного из игроков равен проигрышу другого, называется игрой с нулевой суммой (антагонистической игрой).

Игра называется конечной, если число стратегий игроков конечно, бесконечной, если хотя быу одного из игроков число стратегий является бесконечным.

В игре с полной информацией перед каждым ходом каждый игрок знает все предшествующие ходы и выигрыши. Просчеты в теории игр не рассматриваются.

 

Игроки – это стороны, участвующие в игре (конфликте).Иногда под одним из игроков понимается природа, формирующая условия, в которых необходимо принимать решения.

 

Ходом называется выбор одной из предусмотренных правилами игры стратегий и ее осуществление. В простых (одноходовых) играх понятия хода и стратегии совпадают. Ходы игроков бывают личные (сознательный выбор) и случайные (случайный выбор).

 

Стратегией игрока называется совокупность правил, определяющих выбор варианта действий при каждом личном ходе игрока в зависимости от ситуации, сложившейся в процессе игры.

Стратегия выбираемая игроком сознательно исходя из анализа сложившейся обстановки называется личной (или чистой).

Стратегия игрока называется оптимальной, еслиона обеспечивает данному игроку (обычно игроку А) при многократном повторении игры максимально возможный средний выигрыш или минимально возможный средний проигрыш независимо от поведения противника (могут быть использованы и другие показатели оптимальности).

Оптимальные стратегии характеризуются устойчивостью, то есть ни одному из игроков не выгодно отклоняться от своей оптимальной стратегии.

 

Партия игры – это однократная возможная реализация правил игры (стратегий) игроками.

 

Матричной игрой называется парная игра, осуществляемая по следующим

правилам:

1. В игре участвуют два игрока - А и В;

2. Каждый из игроков обладает конечным набором стратегий (для игрока А - это стратегии А₁, А₂, …..А_m, а для игрока В - это стратегии В₁,В₂,…….В_n);

3. Игра заключается в том, что каждый из игроков, не имея информации о действиях противника, делает один ход (выбирает одну из своих стратегий). Результатом выбора игроками стратегий является выигрыш и проигрыш в игре.

4. И выигрыш, и проигрыш выражаются числами а_ij,которые являютсяэлементами, так называемой платежной матрицы. В частности, выигрыш для игрока А при выборе стратегии А_i, и игроком В – стратегии В_j равен а_ij, а для игрока В – он равен в_ij =-а_ij, то есть является проигрышем.

Платежная матрица (или матрица игры) – является одним из способов задания матричной игры, который называется нормальным. Второй способ задания игры – позиционный способ связан развернутой формой задания игры и сводится к построению графа последовательных шагов игры (дереву игры).

Если условие в_ij =-а_ij не выполняется, то есть каждый из игроков имеет свою платежную матрице, тогдаэтапарная игра является игрой с ненулевой суммой и называется биматричной игрой.

 

Решить матричную (антагонистическую) игру – значит найти для игроков А и В их оптимальные стратегии.

Решение игры связано с матрицей (а_ij) и следующими понятиями:

Нижняя цена игры α=maxmin а_ij (сначала находится минимум в каждой строке, а

I j

потом из полученных минимумов находится максимум). Это гарантированный выигрыш игрока А при любой стратегии игрока В.

Верхняя цена игры β=minmax а_ij (сначала находится максимум в каждом столбце,

J i

а потом из полученных максимумов находится минимум). Это гарантированный проигрыш игрока В при любой стратегии игрока А.

Очевидно α<= β. В случае α=β говорят о цене игры ν=α=β. Соответствующие цене игры стратегии являются оптимальными, а сама игра есть игра с седловой точкой.

 

В случае, когда α<β седловой точки не существует. В этом случаерешение игры ищестся в смешанных стратегиях. Доказано (Дж. Фон Нейман), что конечная матричная игра имеет, по крайней мере, одно оптимальное решение, возможно в смешанных стратегиях.

 

Смешанная стратегия состоит в том, что при повторении игры происходит случайный выбор стратегии из множества смешиваемых стратегий и для каждой смешиваемой стратегии указывается вероятность (частота) ее выбора. В таком случае для каждого игрока указывается вектор частот, с которым следует применить ту или иную стратегию.

Для игрока А это Р=(р₁,….р_m), а для игрока В – это Q=(q₁,…….,q_n), при этом

Σ pi=1 и Σ q_j=1, средний выигрыш игрока А равен Н_А(Р,Q)=Σ Σ а_ij pi q_j

Если вероятность применения стратегии отлична от нуля, то такая стратегия называется активной.

 

Оптимальными смешанными стратегиями Р⁰ и Q⁰ называются стратегии, если выполняется неравенство:

 

Н_А(Р,Q⁰)=< Н_А(Р⁰,Q⁰)=< Н_А(Р⁰,Q)

 

В этом случае Н_А(Р⁰,Q⁰) называется ценой игры и обозначается α=<ν=< β

Первое из неравенств означает, что отклонение игрока А от своей оптимальной смешанной стратегии при условии, что игрок В придерживается своей оптимальной смешанной стратеги, приводит к уменьшению среднего выигрыша игрока А. Второе из неравенств по смыслу аналогично первому с той лишь разницей что касается игрока В.

Решение всякой парной конечной игры с нулевой суммой может быть получено методами линейного программирования.

Сведение матричной игры к задаче линейного программирования

Из свойств оптимальных смешанных стратегий игроков вытекает, что при любой стратегии игрока В для игрока А имеет место неравенство:

 

Σ а_ij p_i>= ν

ⁱ

Обозначая далее

x_i= p_i/ ν

исходное неравенство можно переписать следующим образом

Σ а_ij х_i>=1 и Σ х_i>=1/ν

^{i i}

Поскольку игрок А стремиться максимально увеличить свой гарантированный выигрыш, то задача отыскания решения матричной игры сводится к следующей задаче линейного программирования:

Σ х_i → min

ⁱ

Σ а_ij х_i>=1

ⁱ

Рассуждая аналогичным образом со стороны игрока В – он стремиться сделать свой гарантированный проигрыш минимальным. И вводя обозначения:

y_i= q_i/ ν

и учитывая, что Σ а_ij y_i<=1 получаем двойственную по отношению к

ⁱ

рассмотренной следующую задачу линейного программирования:

Σ y_i → max

ⁱ

Σ а_ij y_i<=1

ⁱ

 

Матричные игры с природой (теория статистических решений)

 

В рассматриваемой (см. выше) теории матричных игр исследуются игры, в которых противник «разумный и злонамеренный» (неопределенность в этих играх состоит в том, что выбор действий противника неизвестен), так и игры, в которых действия противника («природы») неосознанны, пассивны (другой в отличие от первого вид неопределенности). «Природа» действует случайным образом, точнее считается, что ее состояния реализуются случайным образом.

В качестве второго игрока (В), действительно может выступать природа, например: нефтегазовый пласт, природные условия (суша, море, климат и др.), геолого-технологические условия (пористость, проницаемость, высота кровли пласта и т.д.) и др., которые активных действий не предпринимают, а неопределенность состоит в том, с какой вероятностью или шансами реализуются те или иные природные условия.

Матричные игры с учетом последнего типа неопределенности называются играми с природой (или теорией статистических решений).

В игре с природой – пассивный игрок (природа) обычно обозначается как – П.

Суть такой игры состоит в том, что игроку (активному) А требуется выбрать такую чистую или смешанную стратегию, которая является более выгодной, чем остальные.

Предположим, что в платежной матрице мы имеем некоторые а_ij и a_kl такие что, а_ij>a_kl. При этом, выигрыш (а_ij) может быть больше второго (a_kl) не за счёт нашего выбора более удачной стратегии, а за счёт того, что состояние природы П_j выгоднее для нас, чем П_l, в этом смысл удачности стратегии. Поэтому для разрешения этого вопроса необходимо ввести дополнительные показатели, который описывали бы «удачность» или «неудачность» принятия данной стратегии в данной ситуации с учётом общей благоприятности ситуации. С этой целью вводится понятие риска:

1. Платежная матрица задается матрицей выигрышей игрока А.

Риском игрокаА при использовании стратегии А_i в условиях П_j называется разность между выигрышем, который он получил бы, если бы знал П_j, и выигрышем, который он получает в тех же условиях, применяя стратегию А_i. Очевидно, если бы игрок знал заранее состояние природы П_j, он выбрал бы ту стратегию, которой соответствует максимальный выигрыш в данном столбце (максимум столбца j) – это β_j. Тогда риск r_ij есть:

,

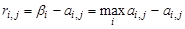где , r_ij ≥ 0.

2. Платежная матрица задается матрицей проигрышей (потерь, убытков) игрока А.

Риском игрока Риском игрокаА при использовании стратегии А_i в условиях П_j называется разность между проигрышем, который он получил бы, если бы знал П_j, и проигрышем, который он получает в тех же условиях, применяя стратегию А_i. Очевидно, если бы игрок знал заранее состояние природы П_j, он выбрал бы ту стратегию, которой соответствует минимальный проигрыш в данном столбце (минимум столбца j) – это β_j. Тогда риск r_ij есть:

r_ij=a_ij - β_j,

где β_j = min a_ij, r_ij≥0

9Поэтому введенное понятие риска является мерой благоприятности состояния природы.

В игре с природой существует два подхода к получению оптимального решения, когда критерии принятия решений зависят от того известны ли нам состояния природы П_j и соответствующие имвероятности Q(П_j) и ли нет.

При первом подходе считается, что состояния природы П_j неизвестны, но известны их вероятности Q(П_j), эта ситуация называется ситуацией частичной неопределенности.

П ри втором подходе наоборот состояния природы известны П_j, но данные о вероятностях их реализации Q(П_j) отсутствуют, такая ситуация называется ситуацией полной неопределенности.

При частичной неопределенности в качестве показателя эффективности (критерия), который необходимо обратить в максимум принимается среднее значение (математическое ожидание) выигрыша игрока А с учетом всех возможных вероятностей Q(П_j). В этом случае за несколько партий мы получим среднее значение выигрыша (математическое ожидание) – критерий Байеса –Лапласа (B-L – критерий):

` ,

где 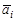– взвешенное среднее.

Оптимальной стратегией А^* = А_i будет та, которая удовлетворяет этому условию.

В результате задача сводится к поиску решения в среднем.

Средний риск:

`

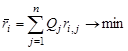
Можно показать, что стратегия максимизации ā_i и минимизации одна и та же. В случае, когда известны вероятности Q₁, Q₂ …. Q_n, при решении игры с природой всегда можно обойтись чистыми стратегиями, не применяя смешанных стратегий, то есть:

средний выигрыш – это среднее взвешенное среднего выигрыша, соответствующее чистым стратегиям и:

Поэтому принятие смешанной стратегии игроком А не может быть выгоднее с любыми вероятностями П_i, чем применение чистой стратегии А* = А_i.

Если в качестве оптимальной стратегии выбирается та из них, для которой величина ā_i обращается в максимум, соответственно в минимум,то такая стратегия называется байесовской .. Эта стратегия является чистой

В этом рассматриваемом подходе, когда вероятности Q(П_j) заранеенеизвестны в теории игр с природой рассматривается ряд вариантов их вычисления:

а) Вероятности Q(П_j) считаются субъективными и определяются экспертами.

б) Ни одно из состояний природы не считается приоритетным и вероятности Q(П_j) считаются равными:

– это – так называемый «принцип недостаточного основания» Лапласа;

В этом случае критерием принятия решения является критерий (критерий Лапласа) и наилучшей стратегией является стратегия, имеющаяя:

_n

max (1/n) Σ a_ij

^j=1

или

 

_n

min (1/n) Σ r_ij

^j=1

 

в) Располагают состояние природы (гипотезы) П_i, в порядке их правдоподобности, тогда вероятности Q(П_j) назначают пропорциональными членам убывающей арифметической прогрессии:

 

Q(П_j): Q(П_j):….. Q(П_j): n :(n-1):…..:1

или

– точечная оценка Фишбена;

которые подставляются в B-L – критерии.

г) существуют статистические данные о состоянии природы, на основе которых можно построить дискретный ряд распределения вероятностей Q(П_j).

В любом из рассмотренных случаев за оптимальное решение принимается та чистая стратегия A_i^*, которая дает средний максимальный выигрыш (минимальный суммарный риск).

В целом, применение этого критерия о выборе решения в условиях неопределенности при рассмотренном подходе превращается в задачу о выборе решения в условиях определенности, только принятое решение является оптимальным не в каждом отдельном случае, а в среднем.

При втором подходе - ситуации полной неопределенности, то естьв случае, когда Q(П_j) неизвестны и не предполагается их вычисление по указанным выше правилам для принятия решений применяют следующие критерии:

Максиминный критерий Вальда

(критерий пессимизма – всегда рассчитывай на худшее, MM - критерий) – худший результат объявляется минимальным выигрышем, то есть:

Критерий Сэвиджа

(любыми путями избежать большого риска) – худшим объявляется не минимальный выигрыш, а максимальная потеря выигрыша по сравнению с тем, чего можно было бы добиться в данных условиях:

Критерий Гурвица

(критерий пессимизма-оптимизма) – степень пессимизма оценивается экспертами критерием α

,

где 0 ≤ α ≤ 1. При α = 1 получаем критерий Вальда.

Критеий Ходжа-Лемана (HL –критерий)

опирается одновременно на MM – критерий и B-L – критерий.

По этому критерию выбор определяется выражением:

_n

Z = max[α Σ a_ij Q_j + (1-α)min a_ij]

^{j j=1 i}

а правило выбора по этому критерию формируется следующим образом.

1. Платежная матрица с элементами a_ij дополняется столбцом, составленным из суммы средних взвешенных (с весом α=const) математических ожиданий и наименьшего результата каждой строки.

2. Отбираются те варианты решений, в строках которого стоит наибольшее значение этого столбца.

При α=1 критерий Ходжа-Лемана переходит в критерий Байеса-Лапласа, а при α=0 максиминным критерием Вальда. С помощью параметра α выражается степень доверия к используемому распределению вероятностей. Если это доверие велико, то приоритет имеет и B-L – критерий, в противном случае предпочтение отдается MM – критерию Вальда.

Критеий Гермейера

ориентирован на величину потерь, то есть на отрицательные значения всех a_ij. При этом, он определяется выражением:

 

Z =max min [a_ij Q_j ]

^{j i}

Правило выбора согласно критерию Гермейера формируется следующим образом: матрица решений с элементами a_ij дополняется еще одним столбцом, содержащим в каждой строке наименьщее произведение имеющегося в ней результата на вероятность соответствующего состояния природы Пj, а затем среди полученных значений этого столбца выбирается вариант с наибольшим значением.

Критерий Гермейера обобщает MM – критерий Вальда: в случае равномерного распределения Q_j=1/n они становятся идентичными.

Критеий произведений имеет вид

_n

Z = max Пa_ij

^{i j=1}

Здесь правило выбора формируется так: матрица решений с элементами a_ij дополняется новым столбцом, содержащим произведения всех результатов каждой строки, и в затем выбирается вариант с наибольшим значением. Критерий имеет смысл когда все элементы a_ij являются положительными.

 

Рассмотрим пример

Предположим, что на территории деятельности нефтедобывающего предприятия открыто и подготовлено к эксплуатации среднее по объему запасов (30 млн. т) нефтяное месторождение. Региональным проектным институтом составлена технологическая схема разработки данного месторождения, предусматривающая его эксплуатацию с помощью трех альтернативных вариантов, отличающихся фондом скважин и их размещением по площади, системами воздействия на пласт, динамикой добычи нефти и жидкости, динамикой капитальных и текущих затрат и другими технико-экономическими показателями.

Практика эксплуатации аналогичных месторождений района показывает, что "истинные" запасы месторождений такого типа могут составлять 20, 25, 30 и в редких случаях 35 млн т. Требуется определить рациональный вариант разработки месторождения исходя из предположения, что вероятности возможных состояний известны (первый случай), вероятности неизвестны, но можно предположить их равенство (второй случай), вероятности отсутствуют (третий случай).

Предположим, что для каждого варианта разработки (каждой стратегии освоения) нефтяного месторождения и каждого состояния природы (объема запасов) рассчитаны значения чистой текущей стоимости, они показаны на пересечении строк и столбцов табл.5.4.

Таблица 5.4.

Поделиться:

Воспользуйтесь поиском по сайту: