 |
Ввод ограничений и граничных условий
|
|
|
|
Задача.
Фабрика «GRM pic» выпускает два вида каш для завтрака - «Crunchy» и «Chewy». Используемые для производства обоих продуктов ингредиенты в основном одинаковы и, как правило, не являются дефицитными. Основным ограничением, накладываемым на объем выпуска, является наличие фонда рабочего времени в каждом из трех цехов фабрики.
Управляющему производством Джою Дисону необходимо разработать план производства на месяц. В приведенной ниже таблице указаны общий фонд рабочего времени и число человеко-часов, требуемое для производства 1 т продукта.
| Цех | Необходимый фонд рабочего времени чел.-ч/т | Общий фонд рабочего времени чел.-ч. в месяц | |
| “Crunchy” | “Chewy” | ||
| А. Производство | |||
| В. Добавка приправ | |||
| С. Упаковка |
Доход от производства 1 т «Crunchy» составляет 150 ф. ст., а от производства «Chewy» - 75 ф, ст. На настоящий момент нет никаких ограничений на возможные объемы продаж. Имеется возможность продать всю произведенную продукцию.
Требуется:
а) Сформулировать модель линейного программирования, максимизирующую общий доход фабрики за месяц.
б) Решить ее c помощью MS Excel.
Формальная постановка данной задачи имеет вид:
 (1)
(1)
Ввод исходных данных
Создание экранной формы и ввод исходных данных

Рисунок 1.
В экранной форме на рисунке 1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка на листе Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи ЛП. Так, например, переменным задачи 1 соответствуют ячейки B4 ( ), C4 (
), C4 ( ), коэффициентам ЦФ соответствуют ячейки B6 (
), коэффициентам ЦФ соответствуют ячейки B6 ( 150), C6 (
150), C6 (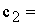 75), правым частям ограничений соответствуют ячейки D18 (
75), правым частям ограничений соответствуют ячейки D18 (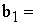 1000), D19 (
1000), D19 ( 360), D20 (
360), D20 (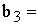 600) и т.д.
600) и т.д.
|
|
|
Ввод зависимостей из формальной постановки задачи в экранную форму
Для ввода зависимостей определяющих выражение для целевой функции и ограничений используется функция MS Excel СУММПРОИЗВ, которая вычисляет сумму попарных произведений двух или более массивов.
Одним из самых простых способов определения функций в MS Excel является использование режима «Вставка функций», который можно вызвать из меню «Вставка» или при нажатии кнопки «  » (рисунок 2) на стандартной панели инструментов.
» (рисунок 2) на стандартной панели инструментов.

Рисунок 2
Так, например, выражение для целевой функции из задачи 1 определяется следующим образом:
· курсор в поле D6;
· нажав кнопку «  », вызовите окно «Мастер функций – шаг 1 из 2»;
», вызовите окно «Мастер функций – шаг 1 из 2»;
· выберите в окне «Категория» категорию «Математические»;
· в окне «Функция» выберитефункцию СУММПРОИЗВ (рис. 3) ;

Рисунок 3
· в появившемся окне «СУММПРОИЗВ» в строку «Массив 1» введите выражение B$4:C$4, а в строку «Массив 2» – выражение B6:C6 (рис. 4);
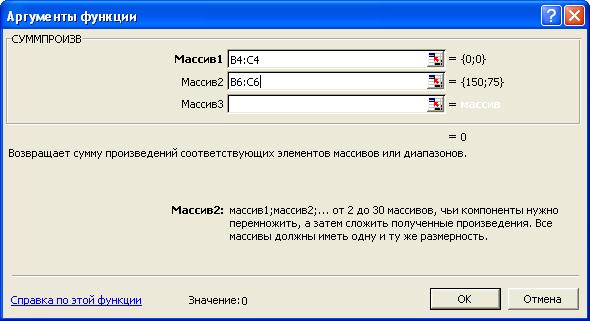
Рисунок 4
Левые части ограничений задачи (1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B13, C13 – 1-е ограничение; B14, С14 – 2-е ограничение и B15, С15 – 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл.1.
Таблица 1.
Формулы, описывающие ограничения модели (1)
| Левая часть ограничения | Формула Excel |
 или или 
| =СУММПРОИЗВ(B4:C4;B13:C13)) |
 или или 
| =СУММПРОИЗВ(B4:C4;B14:C14)) |
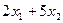 или или 
| =СУММПРОИЗВ(B4:C4;B15:C15) |
Задание ЦФ
Дальнейшие действия производятся в окне «Поиск решения», которое вызывается из меню «Сервис» (рис.5):
· поставьте курсор в поле «Установить целевую ячейку»;
· введите адрес целевой ячейки $D$6 или сделайте одно нажатие левой клавиши мыши на целевую ячейку в экранной форме ¾ это будет равносильно вводу адреса с клавиатуры;
|
|
|
· введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке «максимальному значению».

Рисунок 5
Ввод ограничений и граничных условий
Задание ячеек переменных
В окно «Поиск решения» в поле «Изменяя ячейки» впишите адреса $B$4:$С$4. Необходимые адреса можно вносить в поле «Изменяя ячейки» и автоматически путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме.
|
|
|


